Coordinate Rotation Dlgital Computer(CORDIC)算法

参考：Computer Arithmetic: Algorithm and Hardware Design

原理

角度模式

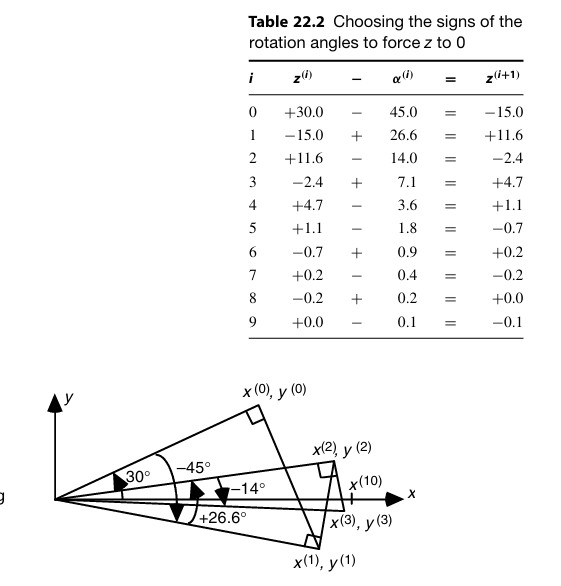
考虑平面直角坐标系下的旋转，如图：

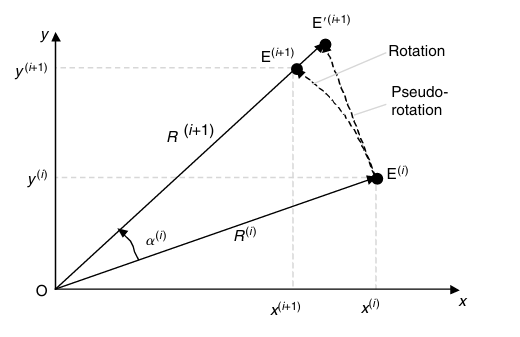
点$E^{(i)}$旋转$\alpha^{(i)}$后得到了点$E^{(i+1)}$

那么假设$E^{(i)}$的坐标为：$E^{(i)}$: $(x^{(i)},y^{(i)})=(R^{(i)}cos\theta,R^{(i)}cos\theta)$

$E^{(i+1)}$的坐标可以表示为：
$x^{(i)+1} = R^{(i)}cos(\theta+\alpha) = x^{(i)}cos\alpha - y^{(i)}sin\alpha \ =\frac{ x^{(i)}-y^{(i)}tan\alpha}{\frac{1}{cos\alpha}}\ = \frac{ x^{(i)}-y^{(i)}tan\alpha}{(1+tan^2\alpha)^{1/2}}$

同理有：
$y^{(i+1)} = R^{(i)}sin(\theta+\alpha) = x^{(i)}sin\alpha + y^{(i)}cos\alpha \ =\frac{ x^{(i)}tan\alpha + y^{(i)} }{\frac{1}{cos\alpha}}\ = \frac{ x^{(i)}tan\alpha + y^{(i)}}{(1+tan^2\alpha)^{1/2}}$

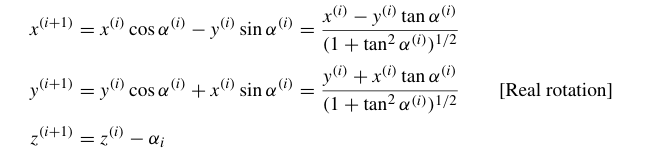
上述公式是一个迭代式，
$ z^{(i)}$表示当前旋转之前向量与x轴的夹角，$ z^{(i+1)}$表示在旋转后与x轴的夹角（顺时针为正）。

现在考虑一种图中的一种伪旋转，对公式2边同时除以$\cos\alpha^{(i)}$,得到$E’^{(i)}$的坐标：

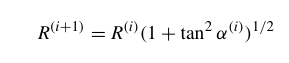
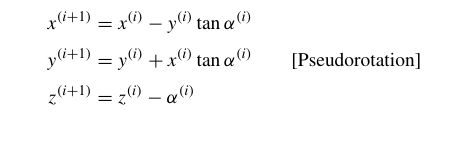
令$x^{(0)}=x, y^{(0)}=y, z^{(0)}=z$，则对于一个m次迭代的真旋转，有：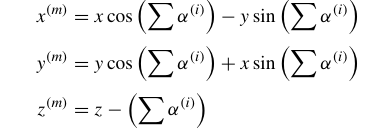

对伪旋转：

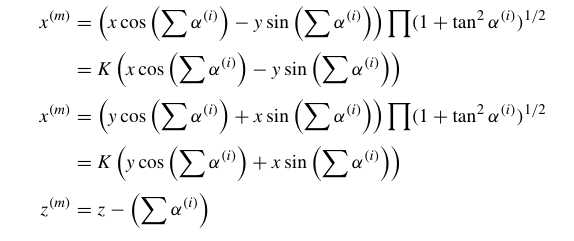
考虑每次迭代的角度选取，如果使$tan\alpha$恰好等于 $2^{-i},i=0,1,2,3…$则上式变为：

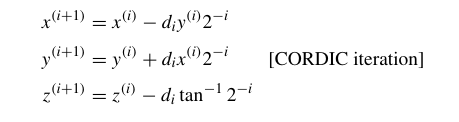
其中$d_i \in {−1,1}$

则每次真旋转迭代的计算可以通过：1次查表，2次移位，3次加(减)法实现。

对于伪旋转，由于每次的角度选取是固定值，因此K为常数，K = 1.646 760 258 121….

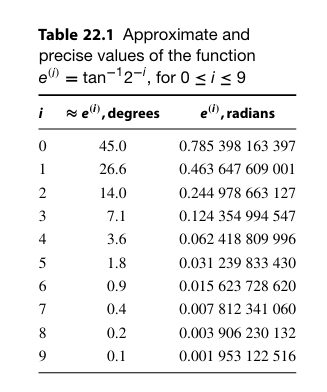
考虑计算 $cosz$,可以令$x^{(0)}=1, y^{(0)}=0, \sum\alpha^{(i)}=z$此时有：

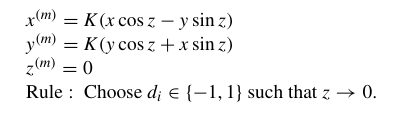
如果计算$cos30^\circ$,可以：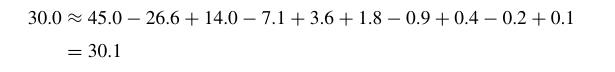

由于表中的角度表示范围达到了$−99.7^\circ ≤ z ≤ 99.7^\circ$,因此可以通过上述方法加上基本三角变化求出任何角的正余弦值。

向量模式

通过令$y\rightarrow 0$,可以计算反三角函数值$tan^{-1}y$,此时，

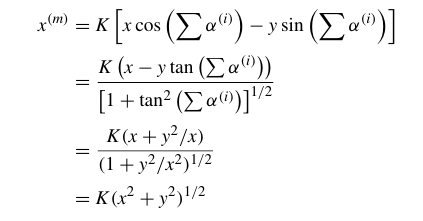
带入

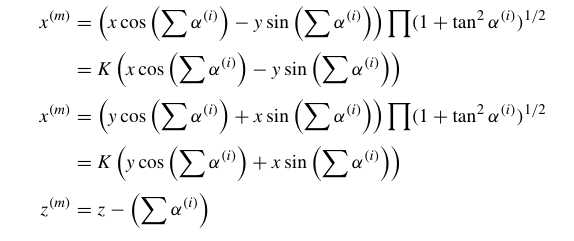
可得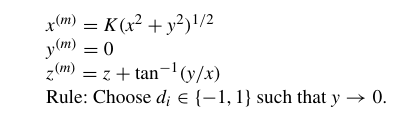

故可以取(1,y),将其旋转到x轴上，此时旋转过的角度即为$tan^{-1}y$

一个简单的python验证程序

import numpy as np
import math

lookuptable = {}

lookuptable[0]=45.0
lookuptable[1]=26.5650
lookuptable[2]=14.0362
lookuptable[3]=7.1250
lookuptable[4]=3.5763
lookuptable[5]=1.7899
lookuptable[6]=0.8951
lookuptable[7]=0.4476
lookuptable[8]=0.2238
lookuptable[9]=0.1119
lookuptable[10]=0.0230
lookuptable[11]=0.0140
lookuptable[12]=0.0070
lookuptable[13]=0.0035




def cordic(value,  mode):
    z = 0
    if(mode==0):
        x =  0.607252935
        y = 0.0 
    if(mode==1):
        x = 1
        y = value
        
    for i in range(13):
        if(mode==0):
            d = np.sign(value)
        else:
            d = -np.sign(y)

        if(d==0):d = 1
        value -= d*lookuptable[i]

        z -= d*lookuptable[i]

        temp = x
        x -= d * y * 2.0**(-i)
        y +=  d* temp * 2.0**(-i)
        # print("y:",y)
        # print("x:",x)

    if(mode==0):
        print("sin:",y)
        print("cos:",x)
    else:
        print("theta:",z)

cordic(4,1)

复杂度分析

对一个n位的cordic运算，若采用纯硬件实现，每一位需要1次查表，2次移位，3次加法，其计算复杂度是$O(n)$这个量级的。

考虑硬件实现，一个最简单的版本是这样的：

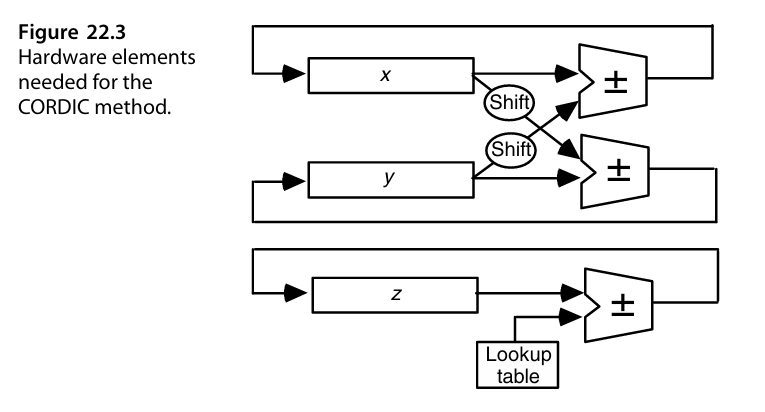
在不考虑优化版本时，图中的加法器可以用串行进位的方式实现，此时，对于k位的操作数，计算需要的时钟周期为$O(k^2)$。

通用版本

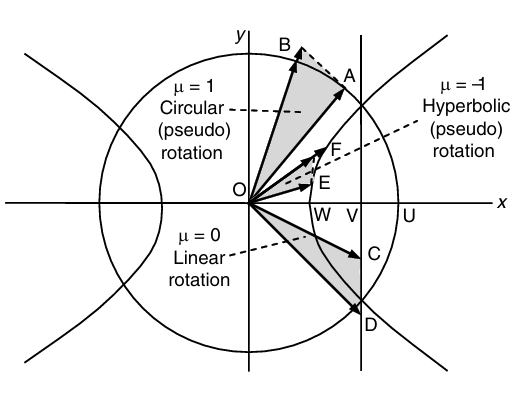
CORDIC算法可以被拓展，用于线性和双曲函数的计算。其通用公式为：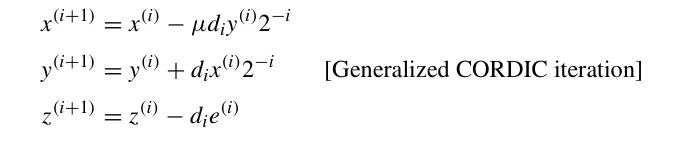

推理过程如下：
参考：（A unified algorithm for elementary functions）

考虑一个从二维直角坐标系到极坐标的非线性映射：

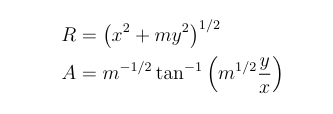
其中R是映射后的向量长度，A是其与坐标轴的夹角。

显然当m取1时，该映射为从直角坐标系到极坐标系的坐标变换。
当m取0时，该变换总是落在一条相同的直线上
当m=-1时，该变换为落在一条双曲线$x^2-y^2=1$上。

事实上，如果将R看作特定曲线与x轴交点到原点的距离，根据上述定义，总是有：
$A = \frac{2S}{R^2}$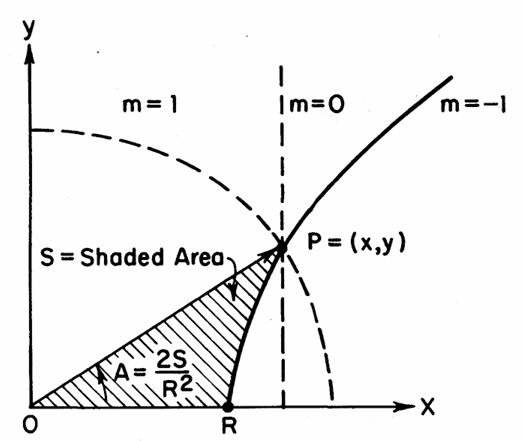

其中S为变换前的点P与点O,R围成的阴影部分面积。

如果给出一个迭代式：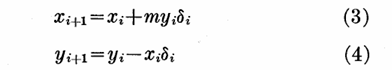

其中$\delta_i$时任意值，而m是映射中的参数。那么每次迭代后的点经过非线性映射后，在极坐标下可以表示为：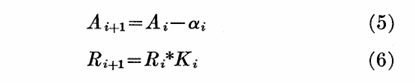

其中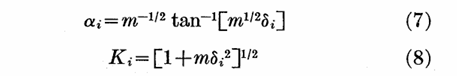

即每次迭代可以看作是一次旋转和放缩。对n次迭代，最后得到的长度和角度为：

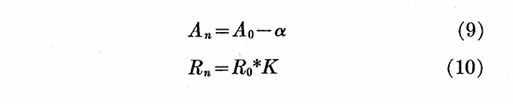
其中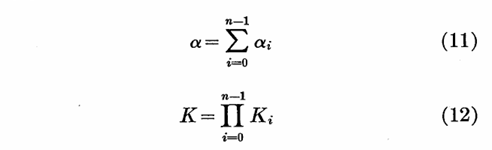

如果再定义一个新的变量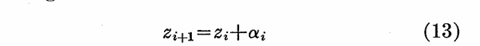

则经过n次迭代后的点经过逆映射后，可以得到其在直角坐标系下的坐标：

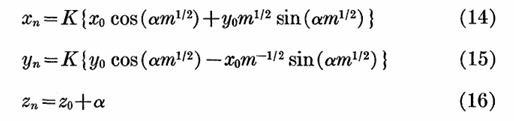
同样的，注意到当m=1时，该迭代式与之前推出的角度模式下的伪旋转迭代式一模一样。

而当m=0时，分别让$y\rightarrow0$和$z\rightarrow 0$,可以得到如下不同的迭代结果：

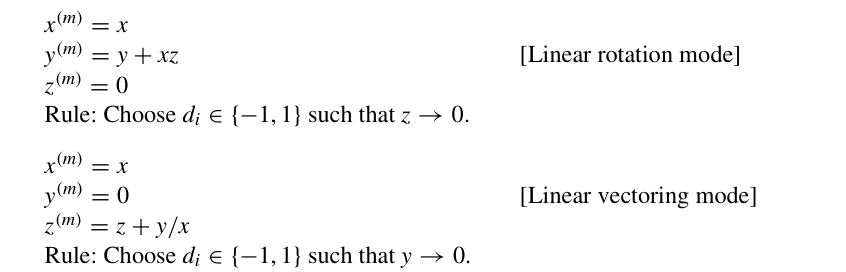
且在m=0时，多轮迭代后的缩放因子为1.

上述公式说明，直线迭代可以用于计算乘法，除法或直接计算一个乘加、除加操作。

而对双曲映射，迭代结果分别为：

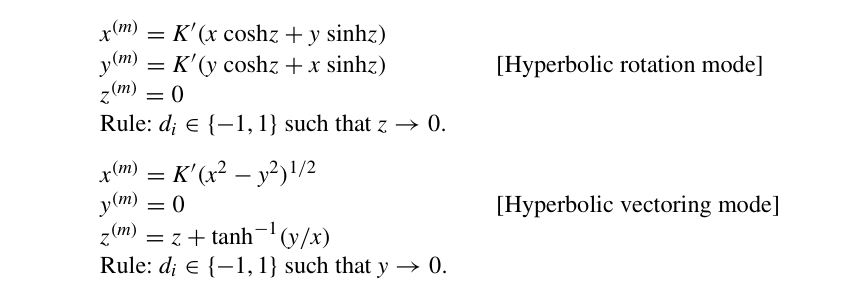
其中缩放因子K'=0.8281593609602。

上述公式说明，双曲映射可以被用来计算双曲正弦，双曲余弦和双曲正切函数。

另外需要注意的是，对于双曲映射，并不总是收敛的，这是因为对于tan函数，总是有：
$tan^{−1}(2^{−(i+1)}) ≥ 0.5tan^{−1}(2^{−i})$

而同样的关系:放在双曲正切中却并不总是成立。

$tanh^{−1}(2^{−(i+1)}) ≥ 0.5tanh^{−1}(2^{−i})$

一个简单的收敛方法为，当迭代次数为:$ i = 4, 13, 40, 121, …,3j + 1$时，该次迭代必须再重复一遍。即：
1,2,3,4,4,5,6,7,8,9,10,11,12,13,13,14….
(收敛性分析在原论文中有比较严格的推导，我懒得手推一遍，这里就不重复了，直接使用其结果)

计算范围为： With these provisions, convergence in computing hyperbolic sine and cosine functions is guaranteed for |z| < 1.13 and in the case of the tanh−1 function, for |y| < 0.81.

此外，以下函数也可以被间接计算出来：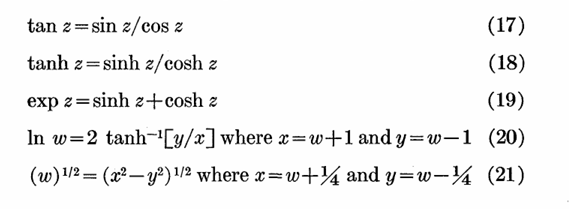

收敛性仿真

写一个简单的双曲迭代来验证上述方法的收敛性：

以cosh为例，以下是一段简单的python代码：


import numpy as np
import math
import matplotlib.pyplot as plt

for i in range(1,20): 
    lookuptable_tanh[i] = math.atanh(2**(-i))
    print(math.atanh(2**(-i)))

def my_tanh(value):
    k=0.8281593609602
    x=1/k
    y=0
    for i in range(1,20):
        if(value)>0:
            d=1
        else:
            d=-1
        
        value = value - d*lookuptable_tanh[i]
        temp=x
        x = x + d*y*2**-i
        y = y + d*temp*2**-i

        # if(i==4 or i==13):
        #     if(value)>0:
        #         d=1
        #     else:
        #         d=-1
        #     value = value - d*lookuptable_tanh[i]
        #     temp=x
        #     x = x + d*y*2**-i
        #     y = y + d*temp*2**-i
    print("my_cosh:",x)
    print("my_sinh:",y)
    print("my_tanh:",y/x)

    return(x,y,y/x)

x = np.arange(-1, 1, 0.01)
# 计算对应的 cosh 函数值
y_numpy = np.cosh(x)

y_custom=[]
for value in x:
    y,_,_ = my_tanh(value)
    y_custom.append(y)

# 绘制图形
plt.plot(x, y_numpy, label='numpy.cosh(x)')
plt.plot(x, y_custom, label='my_cosh(x)')
plt.xlabel('x')
plt.ylabel('cosh(x)')
plt.title('Comparison of cosh(x) functions')
plt.legend()
plt.grid(True)
plt.show()

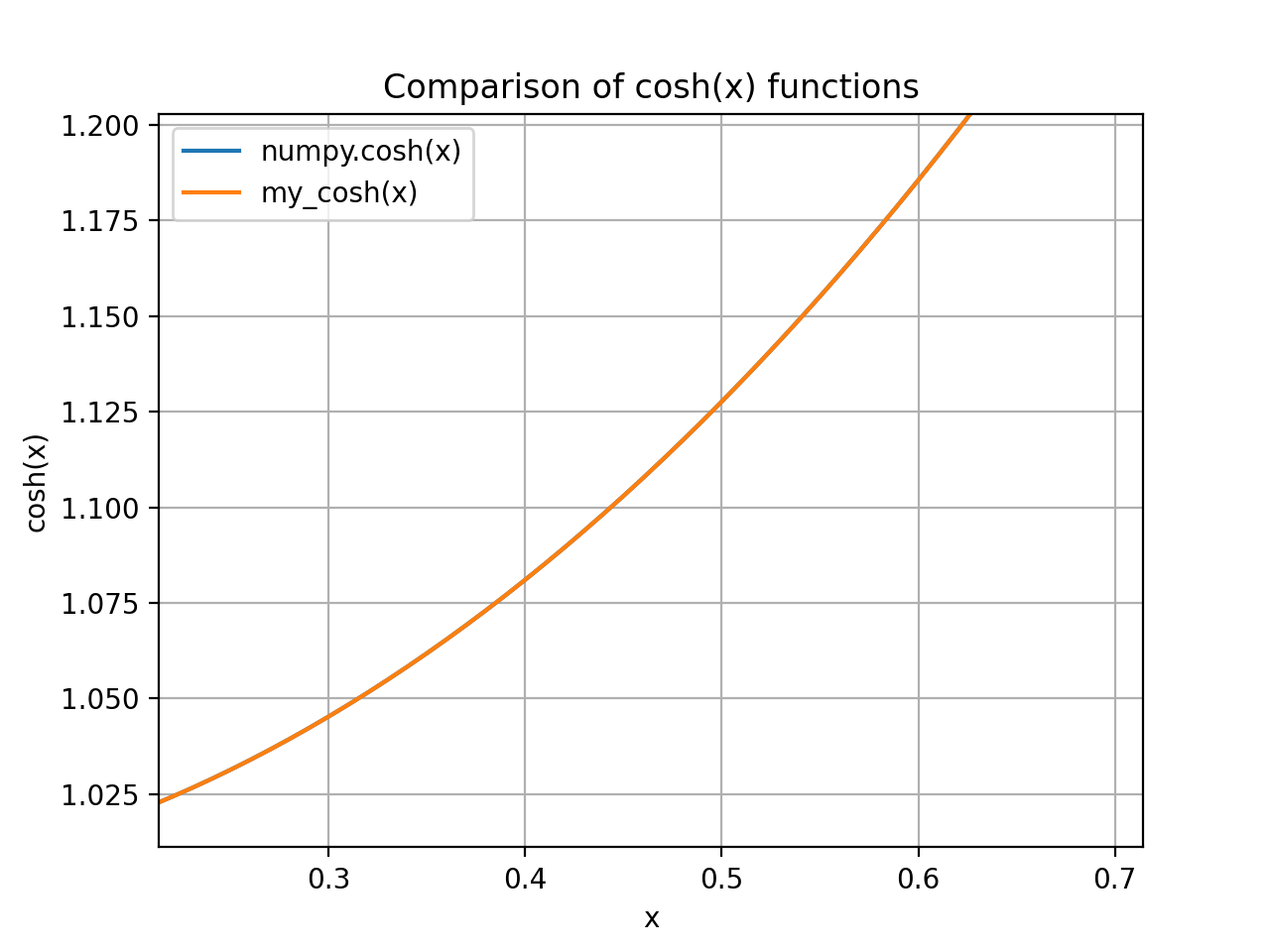
在不用重复第4次和第13次迭代时，结果如下：

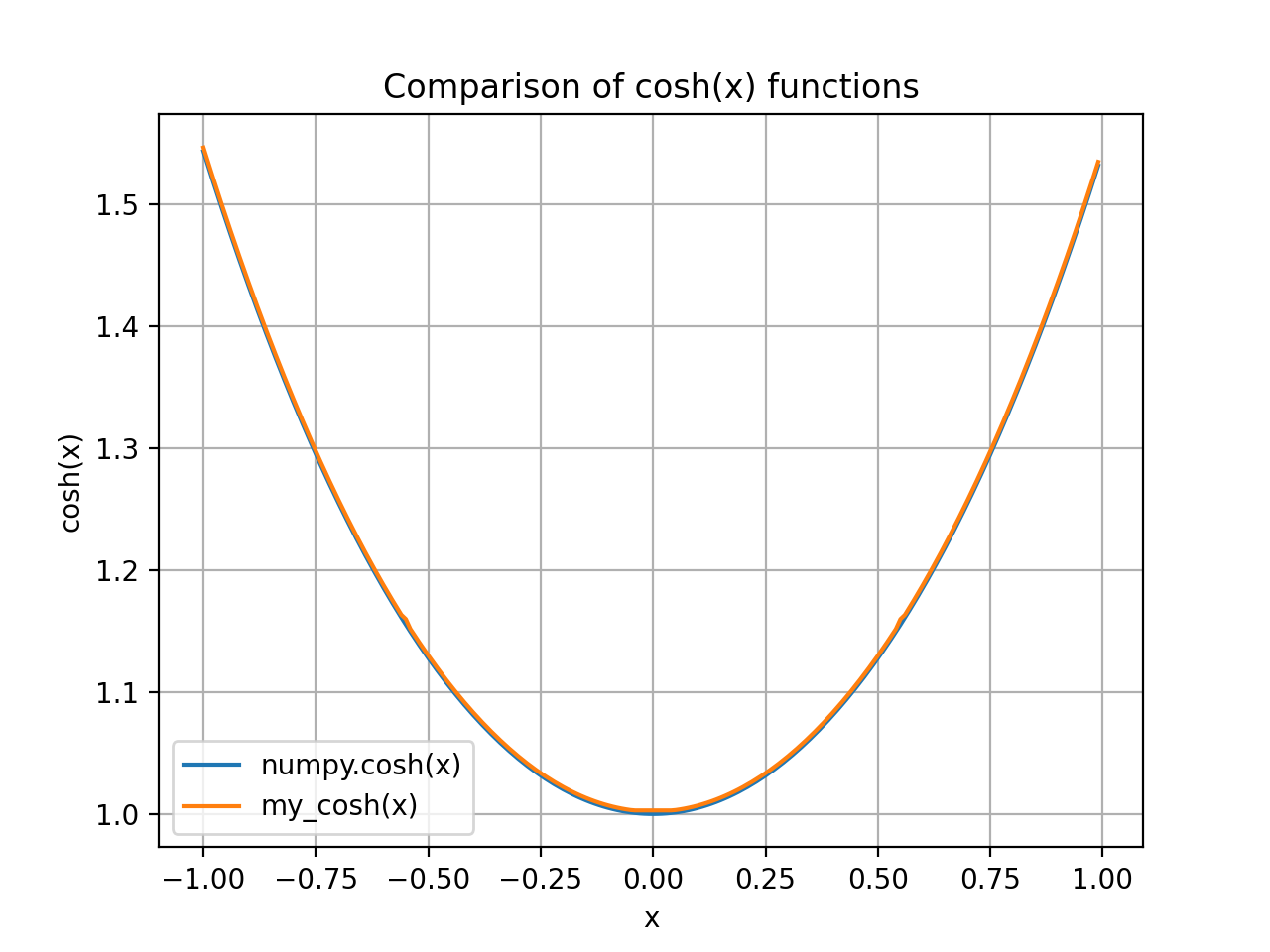
可以看到蓝色线和橙色线不完全重合，局部放大后结果如下：

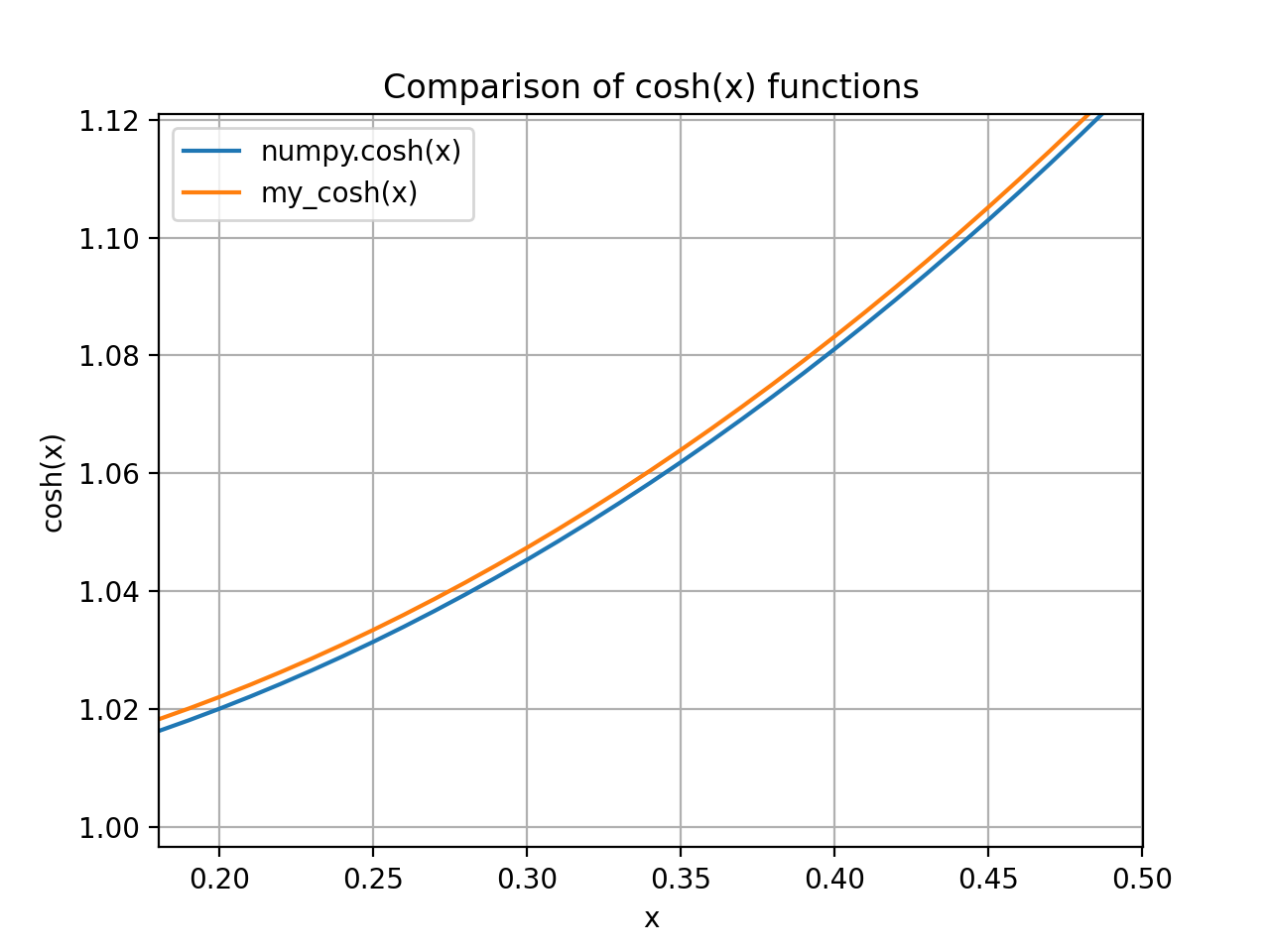
取消对应注释，重复第4和第13次迭代，结果如下：

可以看到蓝色线和橙色线基本完全重合，局部放大后结果如下：

花间一壶酒

CORDIC Algorithm