LSFR

简介

LFSR 全称为Linear Feedback Shift Register, 线性反馈移位寄存器。LFSR 可以用来
产生可重复的伪随机序列，从而被广泛使用在计数器，解码器，密码系统，BIST等方
面。
一般的LFSR分为2种，内部反馈型和外部反馈型的LFSR，如图2–1所示。其中内
部反馈型LFSR又称为伽罗瓦LFSR，而外部反馈型LFSR又称为斐波那契型LFSR。

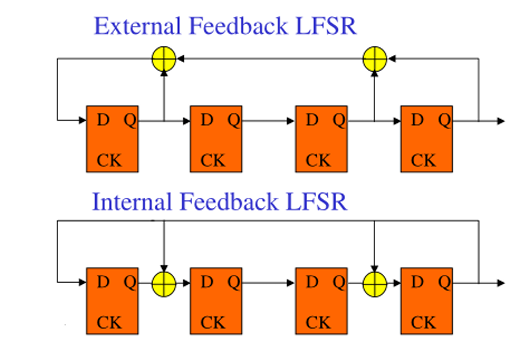
由于伽罗瓦LFSR的逻辑门位于2级寄存器之间，理论上拥有更低的延迟和更高的
频率。

LFSR可以生成具有固定周期的序列，当周期很长时，序列可以看作是近似随机的。

LFSR的周期

LFSR的一个重要特性是其生成序列的周期性。对于一个n位的LFSR，其周期最大为$2^n-1$,这是因为全0的状态会无限循环，从而需要将全0的序列从中剔除。

一个LFSR的特性可以使用反馈多项式来描述。如图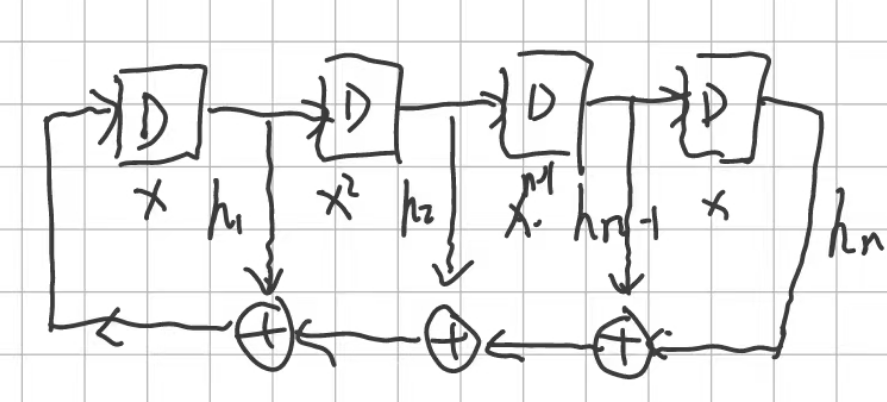

这样的一个LFSR,其反馈多项式可以写作：
$$f(x) = 1 + h_1x+ h_2x^2+\dots +h_{n-1}x^{n-1}+h_nx^n$$

之所以加上1，是因为我们假设原始输入为0000..1,避免全0的状态。

需要注意的是，反馈多项式和用二进制表示多项式的概念是不同的。

反馈多项式代表LFSR的周期特征。具体来说，LFSR的周期数与其反馈多项式的阶数有关。
设$P_n(x)$为n次多项式，满足：
$$min{k:P_n(x)|(x^k+1)}$$
的整数称为多项式$P_n(x)$的阶。即多项式$P_n(x)$仅能被$x^k+1$整除，而对任何${x^m+1|m<k}$,$P_n(x)$均不能被其整除。(这里的整除是GF(2)意义上的整除，在GF(2)域上，加法和减法都等价于模2运算。)

进一步的，称阶数为$2^n-1$的不可约多项式$P(x)$为$GF(2^n)$域上的本原多项式。即本原多项式仅能被$x^{2^n-1}+1$整除，而不能被${x^m+1|m<2^n-1}$整除。同时，本原多项式还无法被分解为$f(x)g(x)$的形式。不可约多项式有点类似于”素数”的概念，即不能被分解为更小的2个多项式的乘积。

LFSR的周期数等于其反馈多项式的阶数。由此我们可以知道，为了构造具有最大周期数的LFSR,我们需要构造反馈多项式为本原多项式的LFSR。

下面是一个寻找本原多项式的python程序：

import sympy

def is_primitive_poly(poly, field_size):
    x = sympy.Symbol('x')
    if poly.degree() != field_size:
        return False
    if not poly.is_irreducible:
        return False
    for i in range(2**(field_size-1),2**(field_size)-1):
        level = sympy.Poly(x**i+1, x, domain='GF(2)')
        if level.rem(poly).is_zero:
            return False
    return True

def integer_to_binary_list(i):
    binary_string = bin(i)[2:]  
    binary_list = [int(bit) for bit in binary_string]  
    return binary_list

def find_primitive_polys(field_size):
    x = sympy.Symbol('x')
    primitive_polys = []
    for i in range(1, 2**(field_size+1)):
        binary_list = integer_to_binary_list(i)
        #print(binary_list)
        symb=0
        for j in range(len(binary_list)):
            symb += binary_list[j]*x**(len(binary_list)-j-1)
        
        poly = sympy.Poly(symb, x, domain='GF(2)')
        #print(poly)
        if is_primitive_poly(poly, field_size):
            primitive_polys.append(poly)
    return primitive_polys

field_size = 9
primitive_polys = find_primitive_polys(field_size)
for poly in primitive_polys:
    print(poly)

该程序的时间复杂度是$O(2^n)$级别的，性能会随着field size设置的增大而急剧下降。

一个更好的办法是利用前人的结果，通过查表寻找需要本原多项式。

下面的网站给出了$GF(2^{10})$以内的所有本原多项式：

https://www.ece.unb.ca/tervo/ece4253/factors.shtml

部分结果如图：

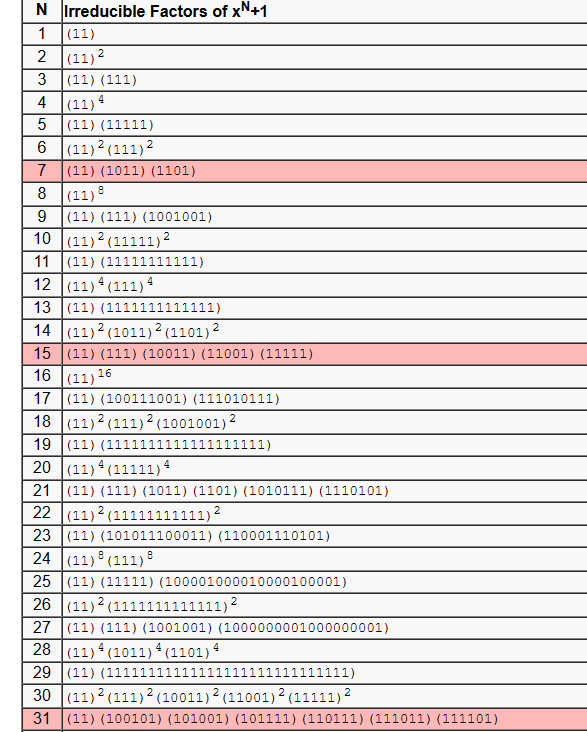
LFSR的应用

(待续)