高等数字集成电路设计

Lecture1 introduction

本节主要对IC产业的发展进行概述，以及介绍一些数字IC设计中的常用概念和基本指标。

IC产业概述

集成电路行业是典型的高附加值行业，具有重资产，高技术附加值，和劳动力密集三重特点。其发展存在典型的周期性: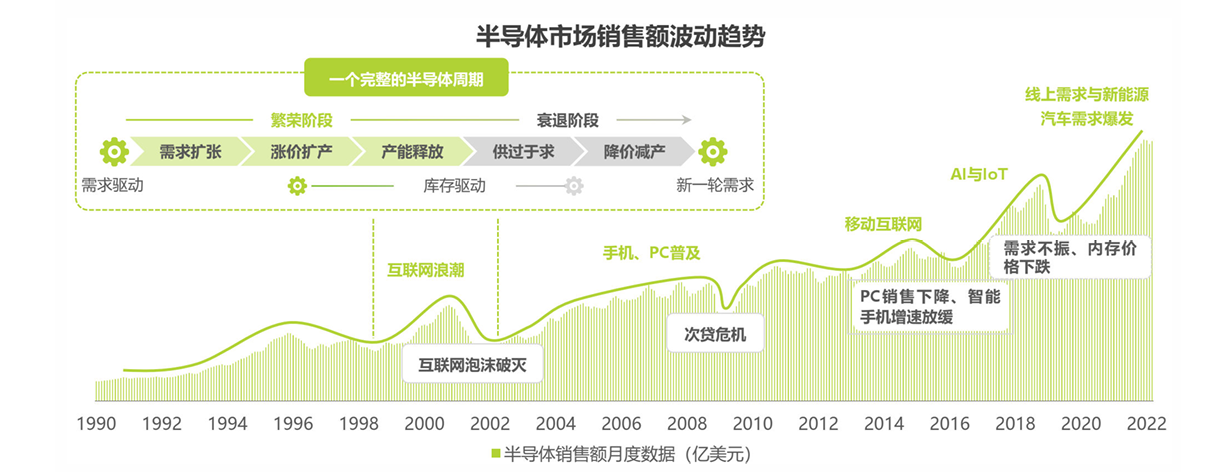

半导体行业的细分领域如下：

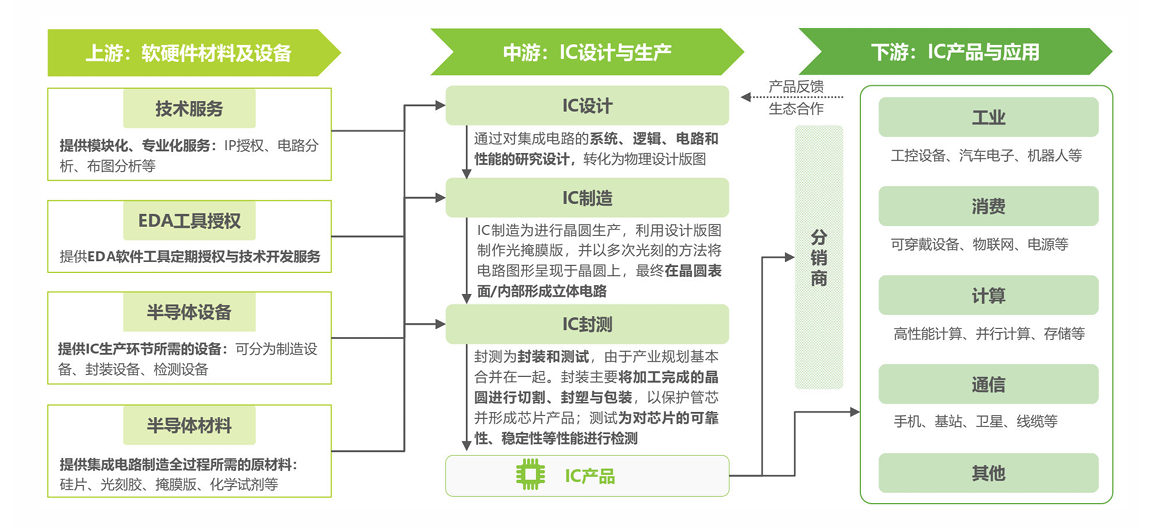
对应中国的产业图谱为：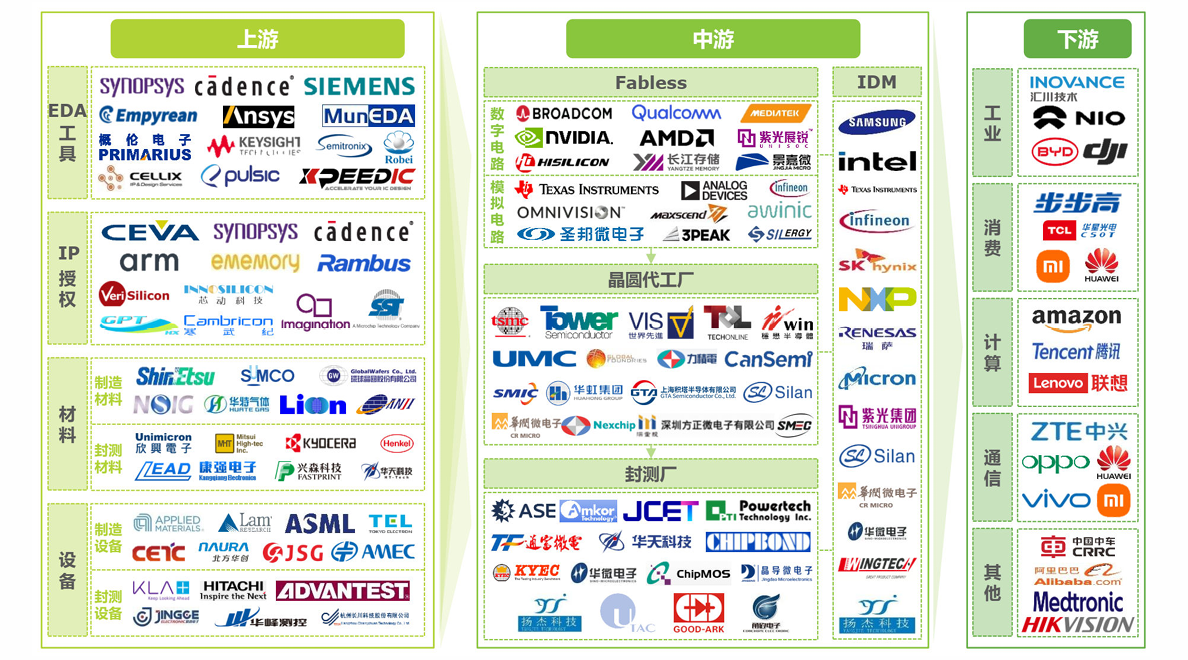

在IC产业的发展历程中，摩尔定律起到核心的推动作用。从芯片制造的角度讲，晶体管尺寸的scaling down能够带来性能，成本和各方面的益处，如下图：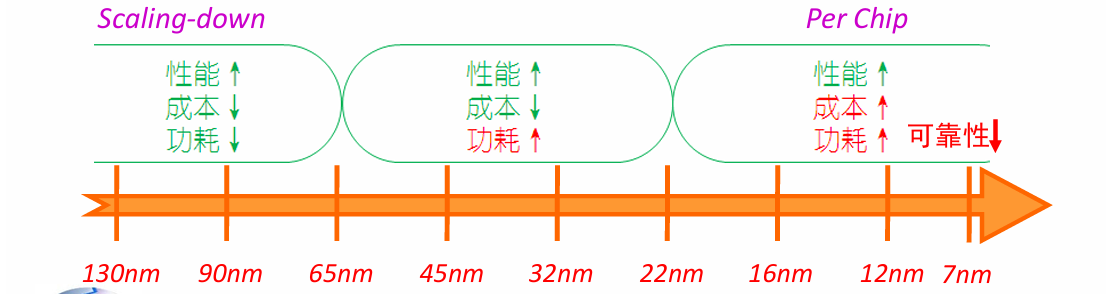

然而随着器件尺寸逼近物理极限，IC工业面临的功耗墙，成本(主要是验证方面成本的急剧提高)及可靠性等各方面的挑战。
各工艺节点下的芯片制作成本如下：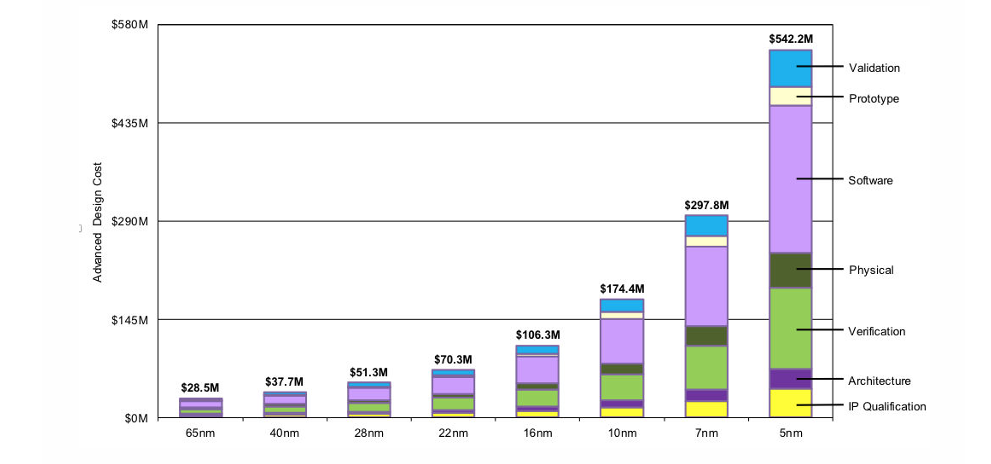

数字IC设计概览

方法学

数字IC设计从业者分为不同层级：架构，逻辑，电路和物理层级，它们负责不同抽象层级的设计，使用不同的设计工具，如下图：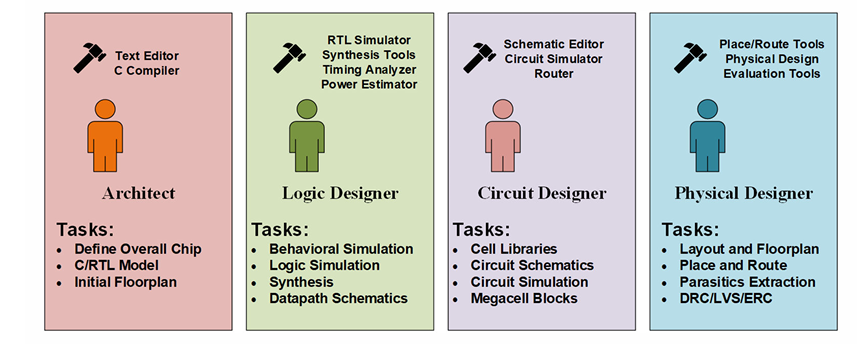

在数字IC的实际实现过程中，又分为全定制设计和半定制设计。其中半定制设计包括标准单元库（standard cell 设计方法）、门阵列（gate array设计方法）。而全定制设计则在器件层面进行性能和功能的优化。半定制的方法在一定程度上降低了设计难度和优化难度，但可能在性能上略逊于全定制设计。如今的大部分IC设计都是基于半定制设计的。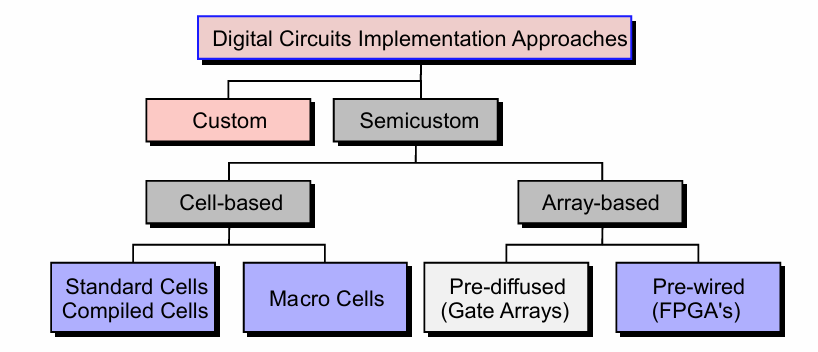

封装

生产出的芯片裸片并不能直接用于生产生活中的直接应用，而需要先进行封装，对芯片进行一定的物理保护，从而增加芯片的可靠性。芯片封装需要考虑以下几个因素：

电气特性，引入尽量小的寄生效应
机械特性：尽量高的稳定性和可靠性
热特性：高效的散热能力
经济性：尽量低的成本

下图展示了封装过程中引入的寄生参数：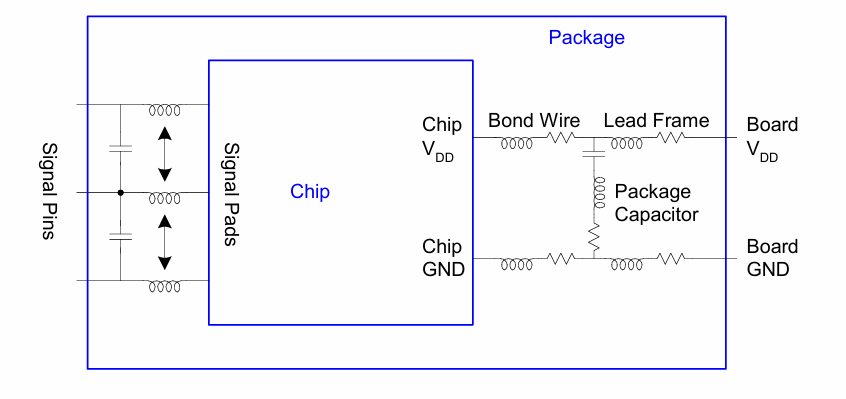

并且，随着IC产业的发展，一些先进封装技术如SiP,3D stacking, Die to Die,Chiplet等技术，脱离了物理保护的范畴，在架构层面实现了芯片性能的提升，从而成为在设计阶段就需要考虑的因素之一。

DFT(defign for test)

如上所述，随着工艺尺寸的scaling down，IC设计面临测试和验证成本的急剧提升。为此引入了DFT技术。一些典型的DFT技术如扫描链(Scan chain)技术，内建自测试BIST(build-in self test),JTAG等。

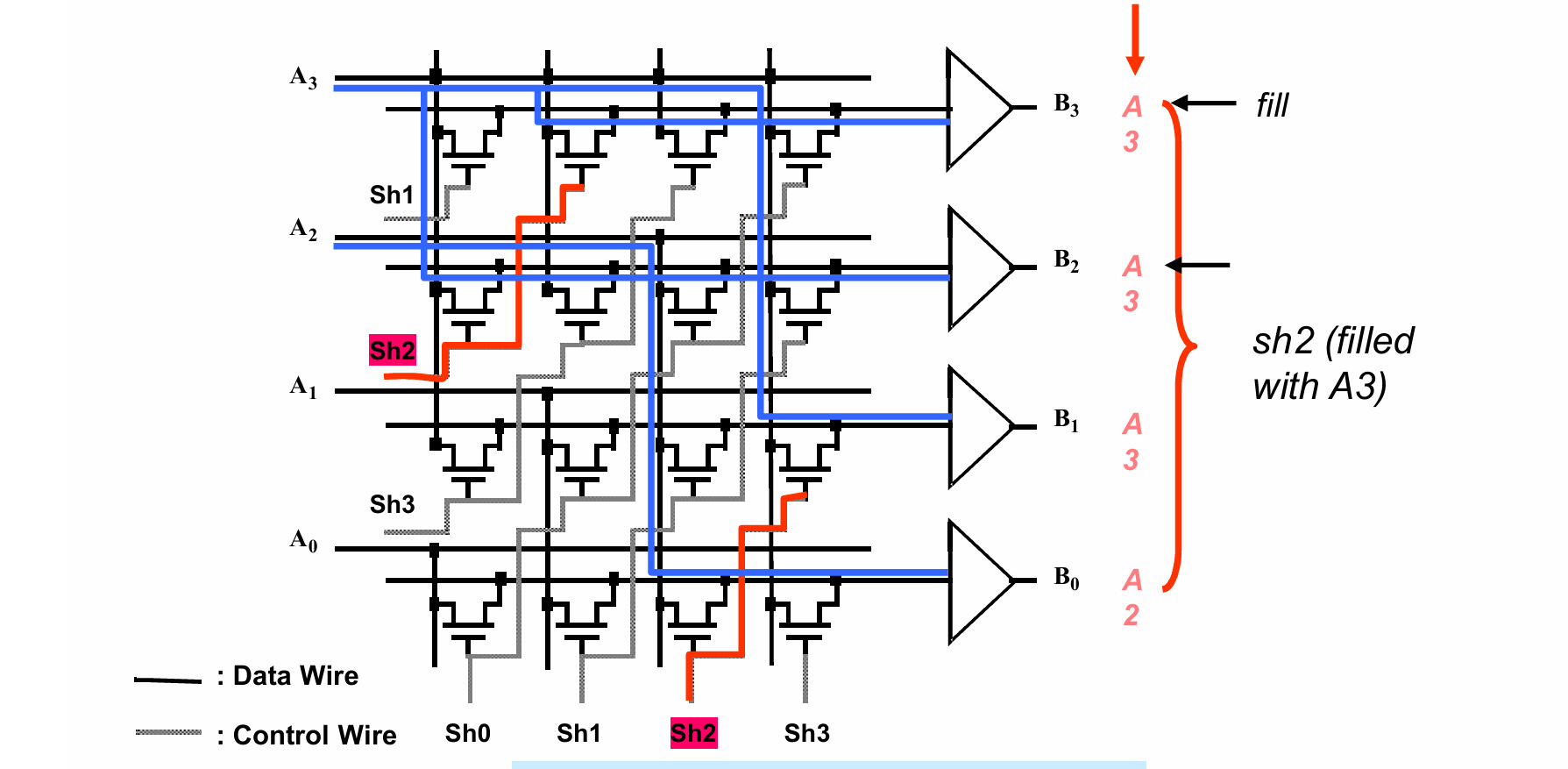
SCAN CHAIN

扫描链技术如下图：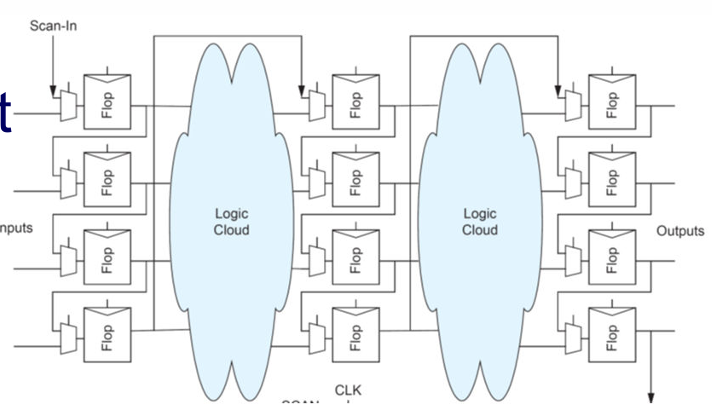

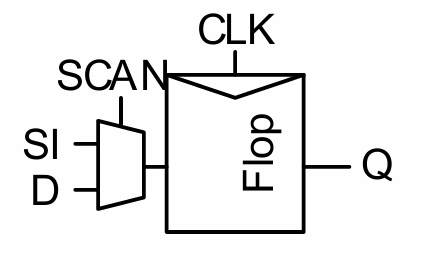
在每个寄存器的输入端口加入一个mux,形成一种scan register,并将每个寄存器的输出端和scan in段串联。

在常规模式下，电路正常工作
在scan 模式下，电路相当于一个shift register,每个寄存器中保存的结果被逐位的移动至输出端口(scan out)，从而能够得到某一周期内电路的所有中间值，进行功能验证。

BIST

待补充

JTAG

待补充

数字IC设计的关心的一些指标

就IC设计而言，最关注的指标无疑是PPA(power,Performance,Area)。这三个指标往往相互约束，需要做出权衡取舍(trade-off)。

而数字IC设计领域，影响PPA的细分指标也有很多，下面分别简要进行介绍。

Fan-in 和Fan-out

fan in 指逻辑门连接的输入，fan-in越大，逻辑门本身的面积越大，同时性能也会越差。

fan-out 指逻辑门连接的输出。fan-out越大，逻辑门需要驱动的下级电路越大，从而速度变慢。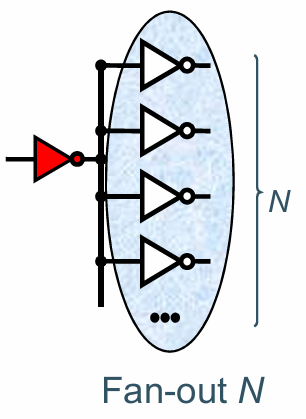

干扰(interference)及噪声(noise)

电路中那些预期之外的电压和电流信号被称为噪声，噪声往往影响电路的性能。

噪声的形成原因多种多样，常见的有平行线路之间的电磁串扰，电容直接的耦合(coupling)等。这些都造成电路信号的不稳定。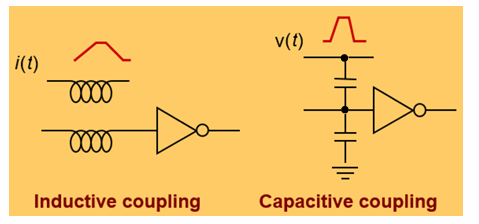

同时，来自电源(VDD)和地(VSS)的噪声也会影响信号。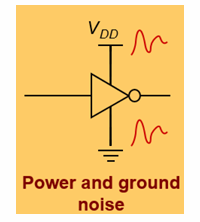

噪声容限 Noise Margins

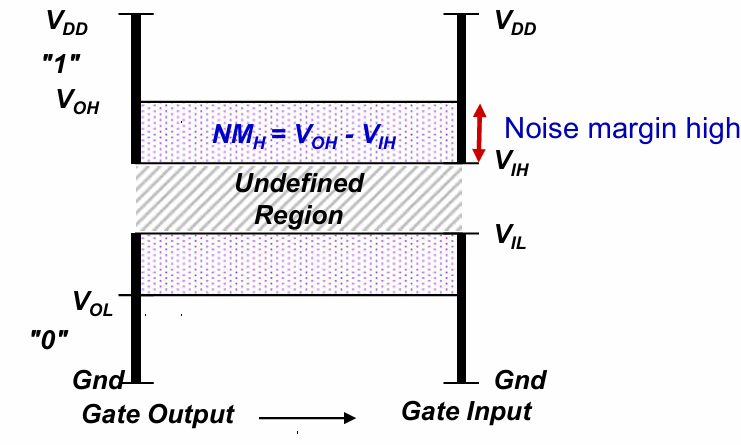
噪声容限一般分为高电平噪声容限$NM_H$和低电平噪声容限$NM_L$,代表电路对噪声的承受能力。它们分别定义为:

$$NM_H = V_{OH}-V_{IH}$$
$$NM_L = V_{IL}-V_{OL}$$

其中$V_{IL}$,$V_{IH}$,$V_{OL}$,$V_{OH}$的定义分别为：

$V_{IL}$（Input Low Voltage）：输入低电平电压。输入信号被识别为低电平（通常为“0”）的最大电压。
$V_{IH}$（Input High Voltage）：输入高电平电压。输入信号被识别为高电平（通常为“1”）的最小电压。
$V_{OL}$（Output Low Voltage）：输出低电平电压。输出信号被识别为低电平（通常为“0”）时的最大电压。
$V_{OH}$（Output High Voltage）：输出高电平电压。输出信号被识别为高电平（通常为“1”）时的最小电压。

传输延迟 Delay

电路的传输延迟参数定义如下图：

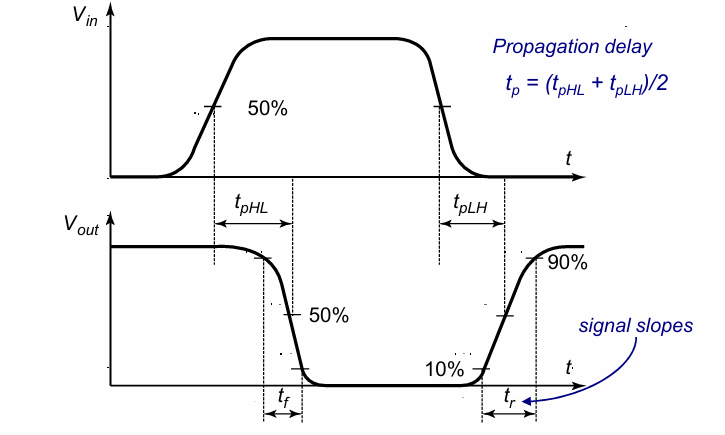
$t_r$：电路从高电平的10%上升为高电平的90%所需要的时间。
$t_f$：电路从高电平的90%下降为高电平的10%所需要的时间。
$t_{pHL}$：输入信号上升为高电平的50%到输出信号下降为高电平的50%所需要的时间。
$t_{pLH}$：输入信号下降为高电平的50%到输出信号上升为高电平的50%所需要的时间。
$t_p$： $t_{pHL}$和$t_{pLH}$的平均值。

能效指标：PDP和EDP

PDP(power delay product)：电路发生翻转期间的平均功耗与传输延迟的乘积,用于衡量电路完成一次计算所消化的能量。单位为焦耳($W\times s$)。

$PDP = P_{av}\times t_p$

EDP(Energy delay product):有时，一个具有低PDP的电路，传输延迟（$t_p$）仍然有可能很大。为了找到在功耗和性能之间的最佳平衡点，可以将Power与Delay的平方相乘。即:

$PEP = P_{av}\times t_p^2 = PDP \times t_p$

在CMOS电路中，PEP一般与电源电压VDD成正比，较低的电压下往往能得到更好的EDP。

Lecture2 Device&Model

本节主要介绍集成电路中的基本器件：二极管和晶体管，以及对其进行分析的基本模型。

二极管Diode

掺杂

硅原子具有4个外层电子，在形成单质(单晶硅)时，每个晶格硅原子与周围的4个硅原子相连，形成正四面体结构：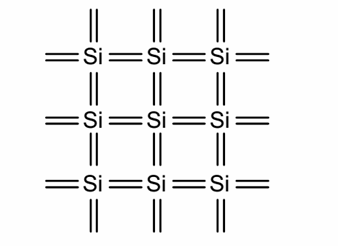

如果对硅单质中掺入少量的3价元素（如硼B），则在一个晶格中存在一个硅原子，其原子核周围缺少一个电子，或者说形成了一个带正电的空穴(free hole)。进行这类掺杂(doping)的半导体材料具有获得电子的特性(acceptors)，称为P(posetive)型半导体。

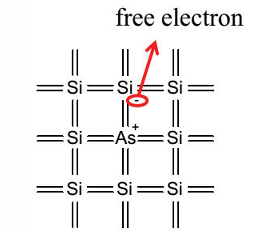
如果对硅单质中掺入少量的5价元素(如磷P,砷As),则在一个晶格中存在一个硅原子，其原子核周围多出一个自由电子(free electron)。进行这类掺杂(doping)的半导体材料具有失去电子的特性(donater),称为N(negetive)型半导体。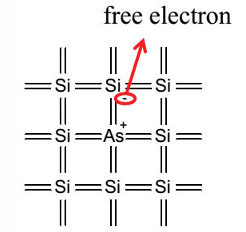

PN结

在将一块P型半导体和N型半导体进行接触之后，由于载流子浓度的不同，N型半导体中的自由电子便会自发向P型半导体的区域进行扩散(diffusion)，对其中的空穴进行填充，形成扩散电流(diffusion current)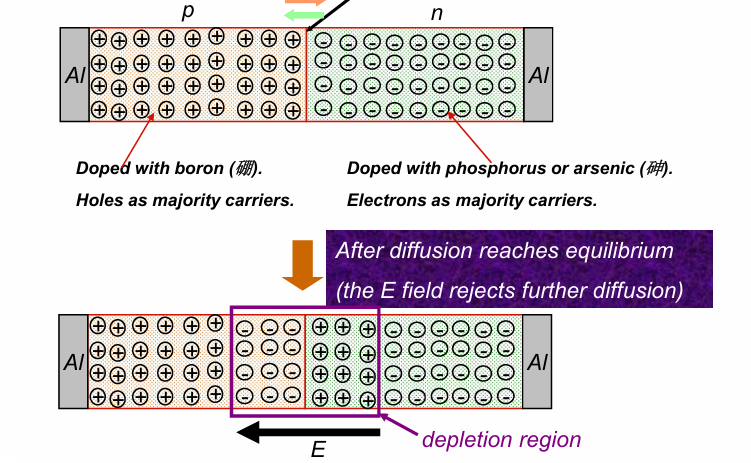

在这个过程中，N型半导体由于失去电子而带正电，P型半导体由于得到电子而带负电，从而在PN结内部形成一个从N指向P的内建电场。在内建电场的作用下，P区的电子反过来向N区运动，形成漂移电流(drift diffusion)

在自然条件下，PN结附近的扩散电流和漂移电流达到动态平衡。那些自发失去和得到电子的区域称为耗尽区(depletion region)。

在扩散作用达到平衡后形成的耗尽区具有如下特点：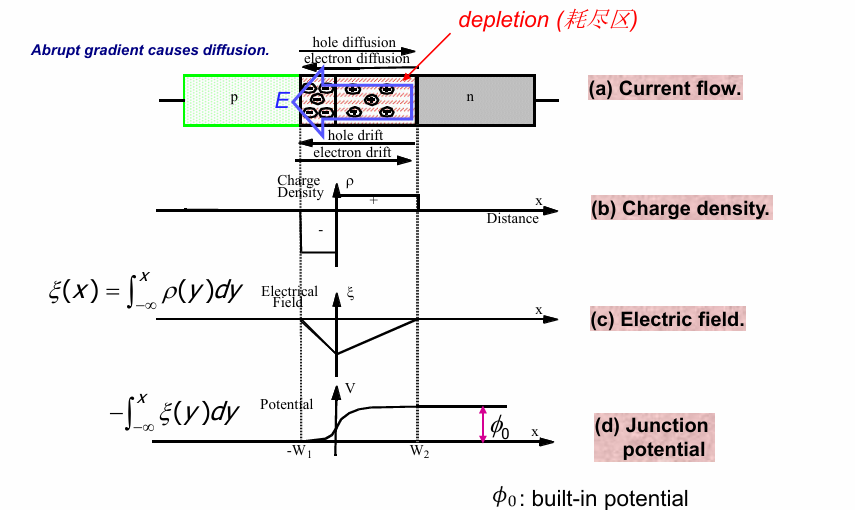

电子/空穴的密度均匀分布。
由于场强是电荷密度的积分，电子/空穴的均匀分布引起电场强调的线性分布。
由于电势是场强的积分，PN结中内建电势随坐标呈现递增分布。

耗尽区中内建电势的存在，会阻止载流子的运动，从宏观上看，降低了材料的导电能力。

偏置

二级结的构成为一个PN结和连接它们的金属，如下图：

其电路符号为一个顶端带有一横线的三角，横线画在N型半导体的位置。

正偏

将二极管的P区连接电源的正极，N区连接电源的负极时，称为正偏(forward bias):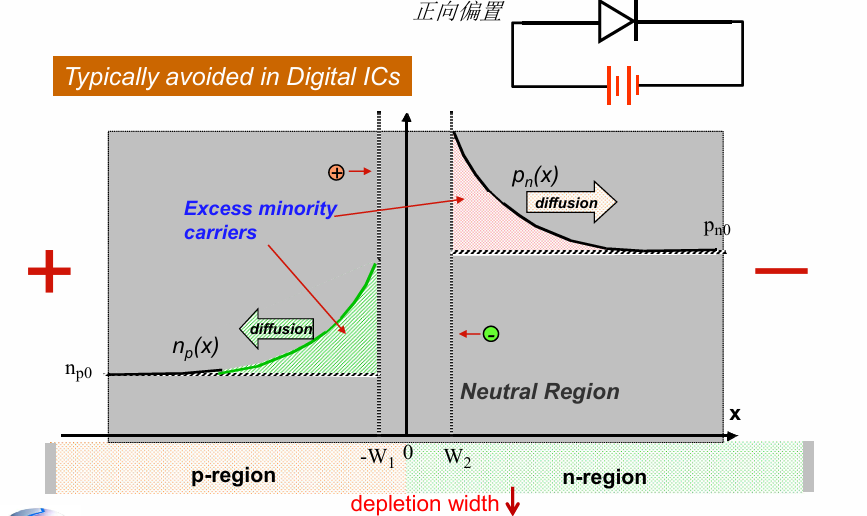

正偏后，施加使得PN结内部的内建电势下降，耗尽区的宽度减小，从而减小了载流子通行的难度。P区的大量空穴和N区的大量电子(这是由掺杂浓度决定的，即空穴在N中为多子，电子在P中也为多子)能够成功穿过耗尽区，从而形成电流。此时占据主导的是扩散电流,导电主要由器件中的多子完成，电流较大。

反偏

将二极管的P端连接电源负极，N端连接电源正极，称为反偏(reverse bias):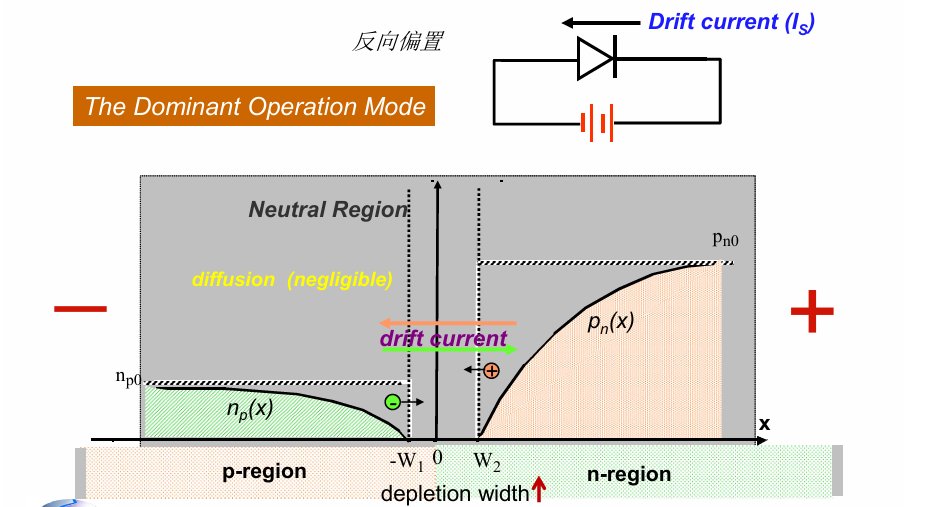

反偏后，外加电源强化了二极管内部的内建电场，从而使载流子穿过耗尽区的难度增加，只有P区中的少数电子和N区中的少数空穴在电场作用下穿过耗尽区，形成电流。此时占据主导的是漂移电流，导电主要由器件中的少子完成，电流较小。

I-V特性

二极管的电流公式为：
$$ I_D = I_s(e^{\frac{V_D}{\phi_T}}-1)$$

其中$\phi_T=\frac{kT}{q}=26mV$

$I_s$为饱和电流，与二极管的掺杂，PN结面面积有关。

在一定情况下也可作一阶近似：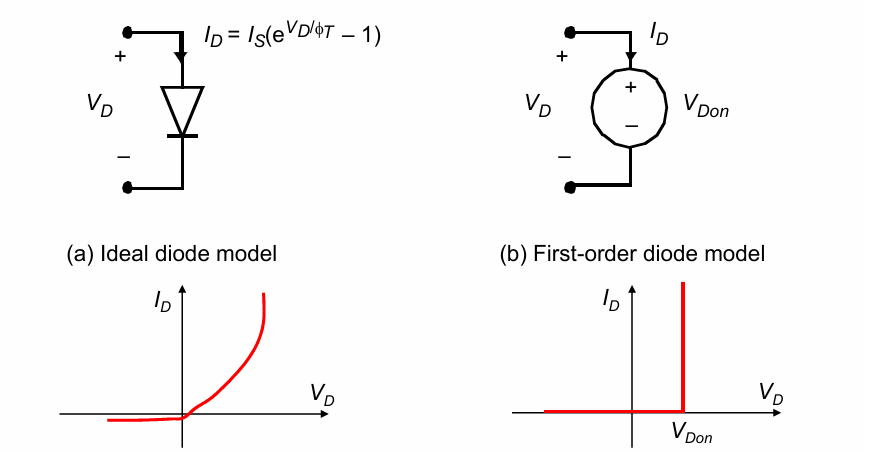

结电容

PN结电容公式为：

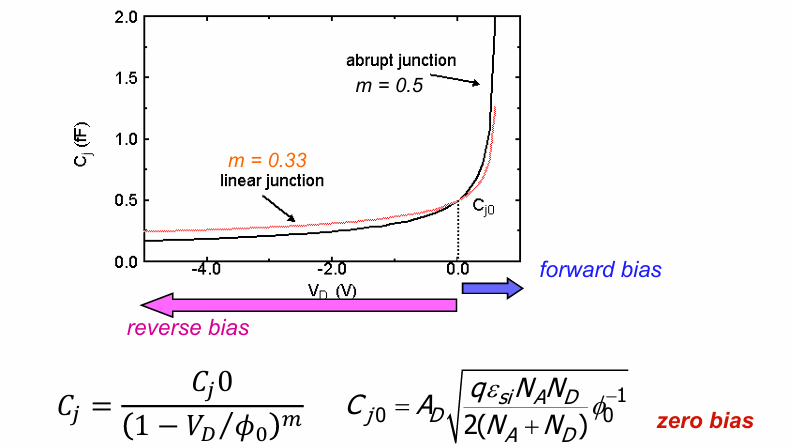
通过对上述公式定性分析可知：施加正偏电压，$C_j$的分母减小，整体结电容增大。一种理解角度是，正偏后耗尽区减小，相当于减小了平行板电容器的间距，从而增大了电容。

MOS晶体管的静态模型

MOS器件的剖面图如下：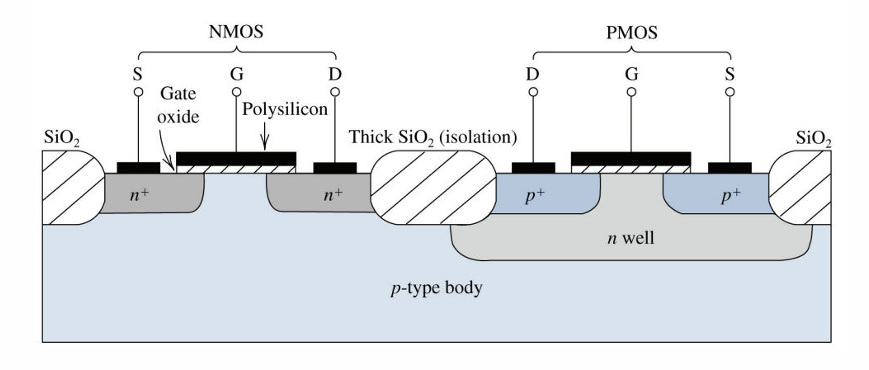

一个晶体管一般可以抽象成一个开关，当gate端施加足够大的电压(超过阈值电压)，则开关打开。

阈值电压

晶体管的gate端可以看作一个平板电容，当施加电压足够高时，在下方的衬底中感应出一定的电荷，形成导电沟道。

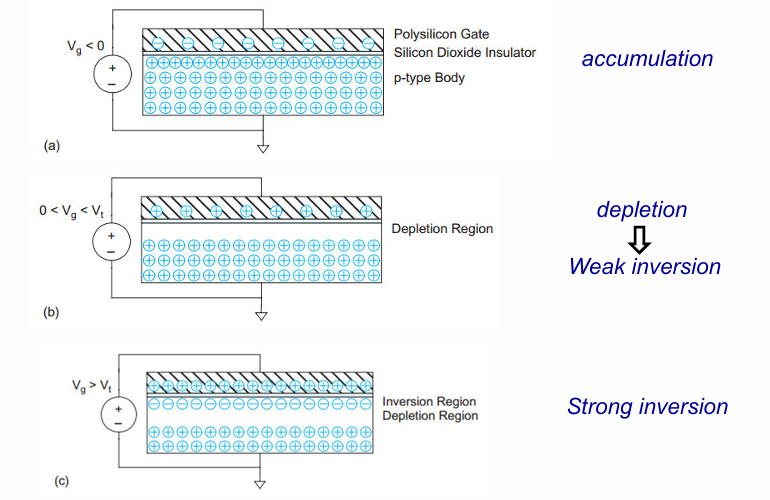
阈值电压的计算公式：
$$V_T = V_{T0} + \gamma (\sqrt{|-2\phi_F+V_{SB}|}-\sqrt{\phi_F})$$

其中：$V_{SB}$是源和沉底之间的电压，$V_{T0}$是$V_{SB}=0$时的阈值电压，由制作工艺决定。$\phi_F$是费米能级。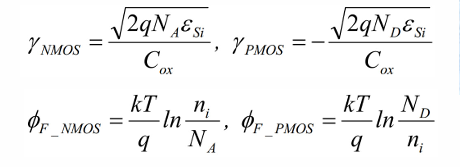

体偏效应

通过上述公式我们可以知道，阈值电压与体源电压有关，从而可以通过条件body端的电压实现阈值电压的条件。这样的方法常被用于低功耗技术中。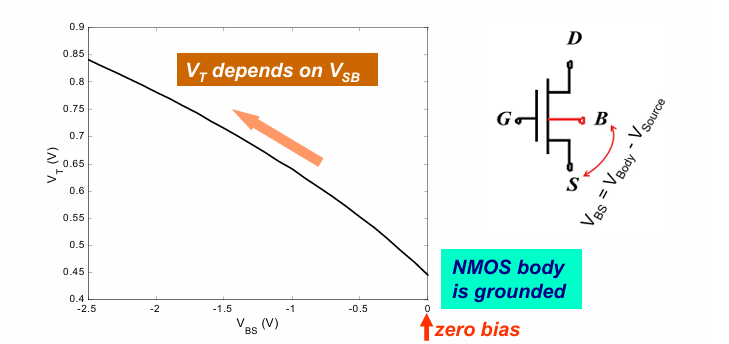

短沟道效应 short channel effet

随着晶体管尺寸的scaling down,器件的沟道长度逐渐缩短，由于工艺导致源漏之间的耗尽区变得接近，使得阈值电压降低，影响晶体管的开关特性。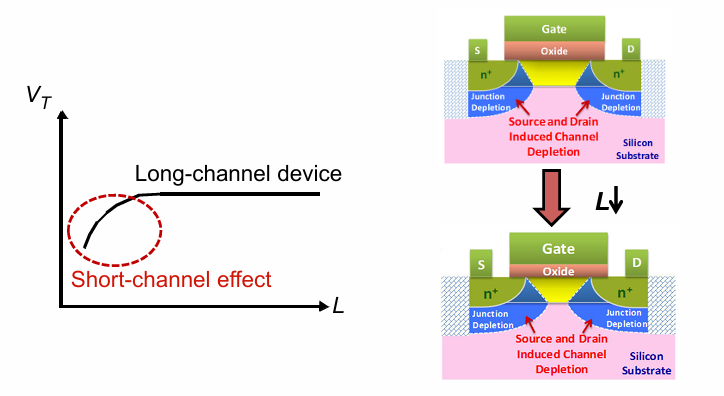

漏致势垒降低效应（DIBL）

Drain-induced barrier lowering：在经典的长沟道器件中，阈值电压的值与漏区电压无关。然而在短沟道器件中，由于晶体管在工作时会给漏级施加电压，从而在D-B之间形成了一个反偏的二极管。这个反偏的二极管增大了漏极的耗尽区宽度，使其与源极的耗尽区进一步接近，从而进一步缩小了导电沟道的长度，使得阈值电压下降。

DIBL本质也是一种短沟道效应。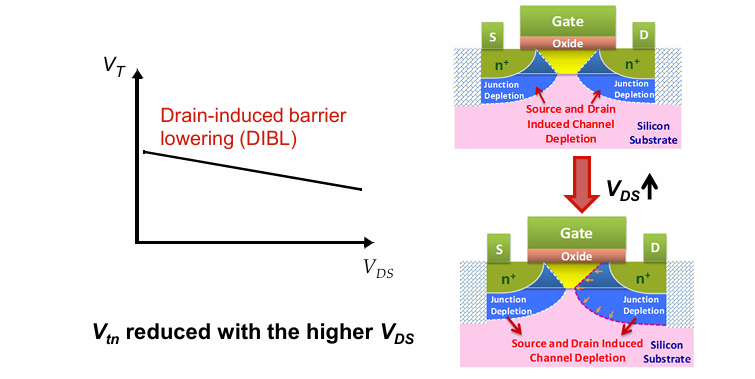

窄沟道效应 narrow channel effet

不同于短沟道效应，窄沟道效应是指当晶体管的沟道宽度(不是长度)变窄时，阈值电压增大的一种现象。这是由于窄沟道的gate端容易与场氧化层重叠，形成更大的GATE电容。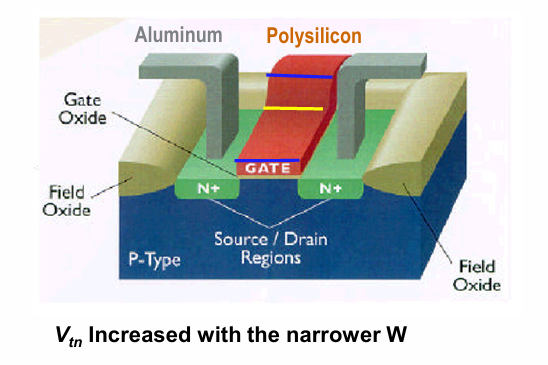

对晶体管的建模

晶体管可以被看做是个 G,S,D,B的3端器件。在使用时，一般NMOS的衬底默认会接VSS,PMOS的衬底接VDD，从而简化为一个G,S,D的3端器件。在G S间的电压负责控制晶体管的开关，DS间的电压负责控制管子电流的流通。

线性区

当晶体管满足：

$$V_{GS}> V_T$$
$$V_{DS}< V_{GS}-V_T$$

管子工作在线性区，此时晶体管的电流大小满足：

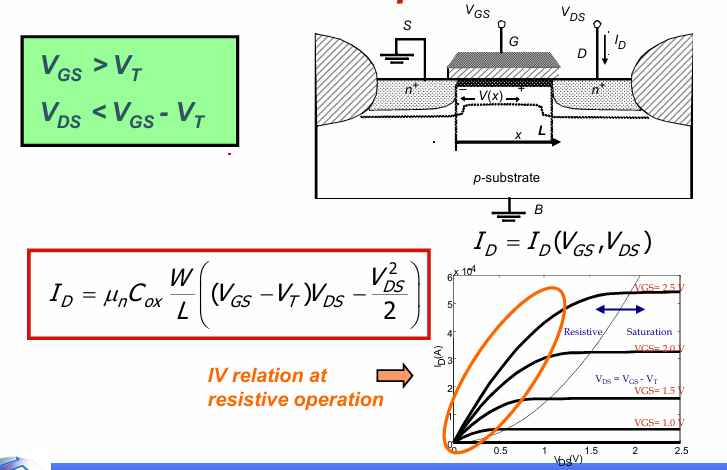
饱和区

当晶体管满足：
$$V_{GS}> V_T$$
$$V_{DS}\geq V_{GS}-V_T$$

电流不再随$V_{DS}$增大而增大，而是只与$V_{GS}$有关：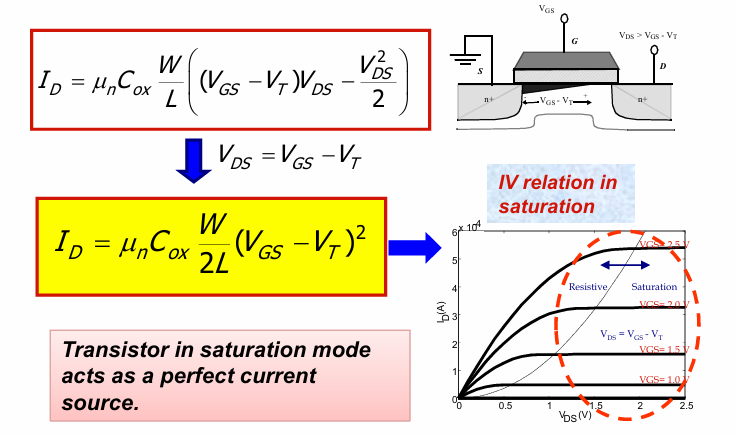

此时的晶体管可以被看做是一个理想电流源。

沟道长度调制 Channel Length Modulation

如下图，当$V_{DS} > V_{GS}-V_T$时，靠近漏区部分的沟道实际上会无法感应出反型电荷而产生夹断(pinch-off)。这将导致晶体管的有效沟道长度减小。而晶体管的电流与沟道长度L成反比。因此实际的电流会增大。通过添加一个参数$\lambda$来修正这种沟道长度调制效应：

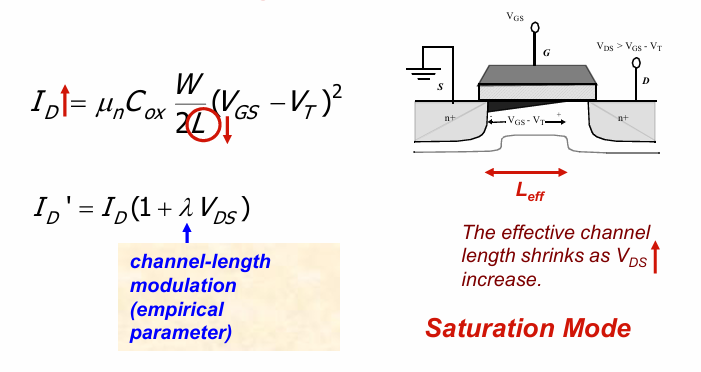
速度饱和 Velocity Saturation

一般来说，载流子的速度正比于电场强度，但是当速度过大时，会因为载流子间的散射效应而趋于饱和，不再满足线性关系。在源漏电压不变的情况下，沟道越短，沟道间的电场强度越大，从而越容易达到速度饱和。

而对同一器件，则存在一个饱和电压$V_{DSAT}$,当源漏电压大于该值是，出现速度饱和。速度饱和会降低饱和区电流。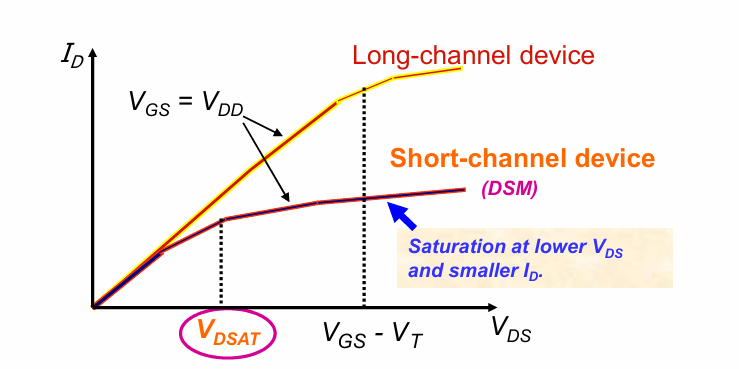

电流公式

结合上述分析，可以分别得到长沟道器件和短沟道器件的电流公式：

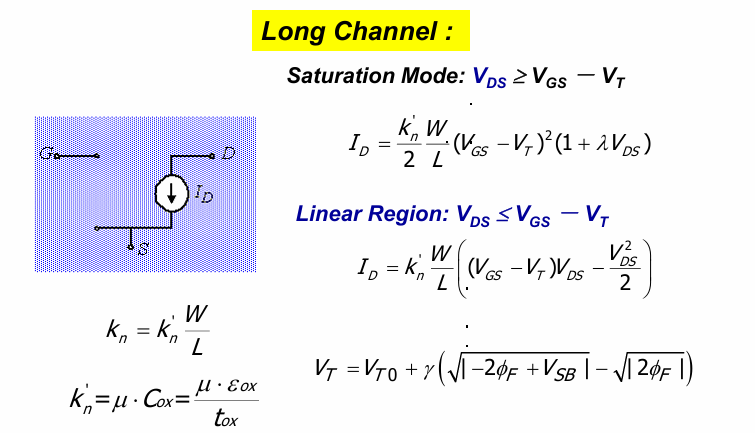
电阻计算

MOS器件的等效电阻可以用如下公式计算：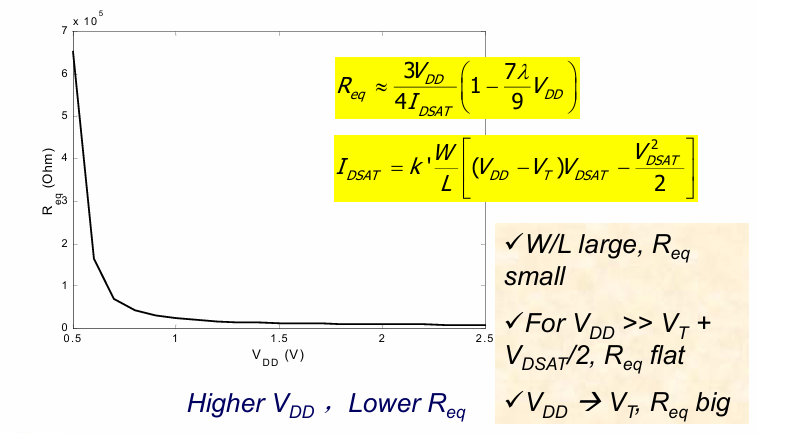

可以看到，同样的器件，在VDD减小的情况下，等效电阻急剧增大。这也是阻止器件的VDD无法随器件尺寸同步scaling down的一个原因。

晶体管的动态模型

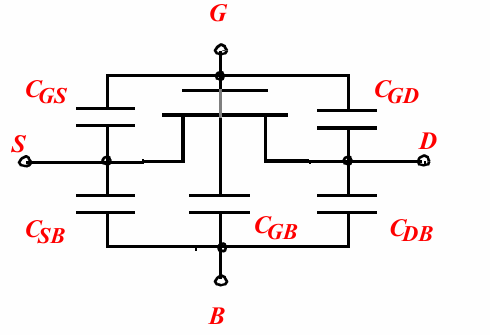
作为一个4端器件，MOS管的电容主要由3部分组成：

结构电容
沟道电容
结电容

下面依次进行分析：

结构电容

这部分的主要成因是MOS管在实际生产时，源和漏会向栅下方扩展一个$x_d$的长度，引起了栅和源漏之间的寄生电容：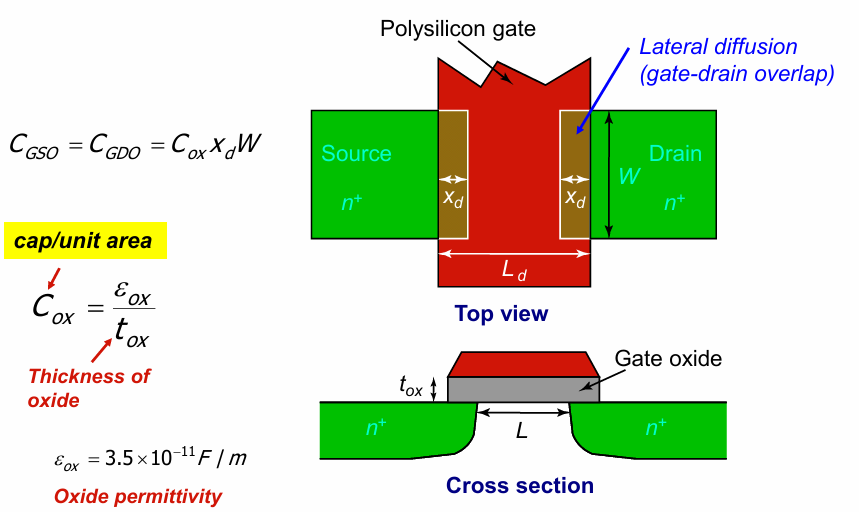

沟道电容

向栅极施加电压，在下方形成导电沟道，这个过程也是电容充电的过程。在这个过程中，gate 端与S,D,B间形成的电容大小与晶体管的工作状态有关，总结如下：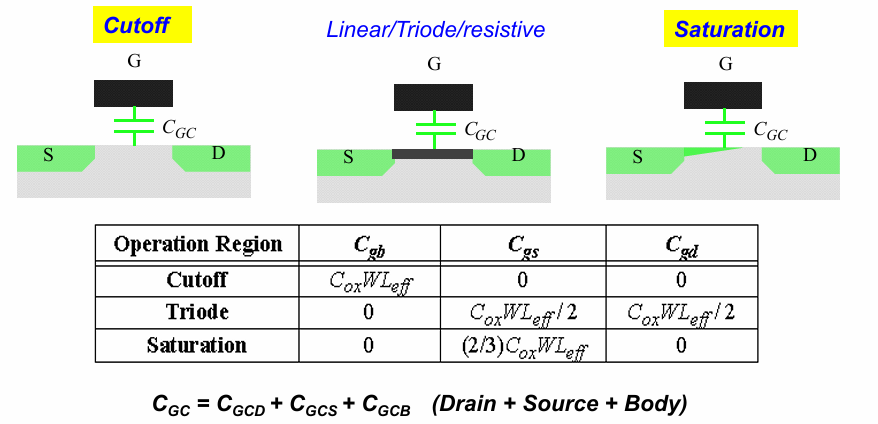

结电容/扩散电容

最后一部分电容的形成原因如下：考虑一个NMOS，其制造是在一个P衬底上挖出2个N well,这样源漏和衬底之间实际上存在一个PN结，这个PN结在D极施加电压时是反向导通的，但是也具有一定的电容。此外因为MOS管实际是一个立体的结构，源漏区除了与底板之外，与侧壁之间也会形成PN结。

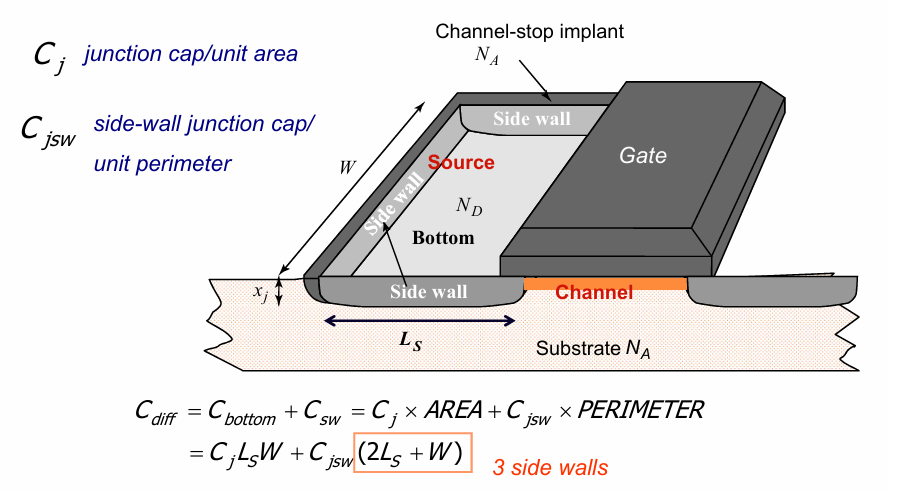
总结上述电容，就可以得到晶体管的电容模型：

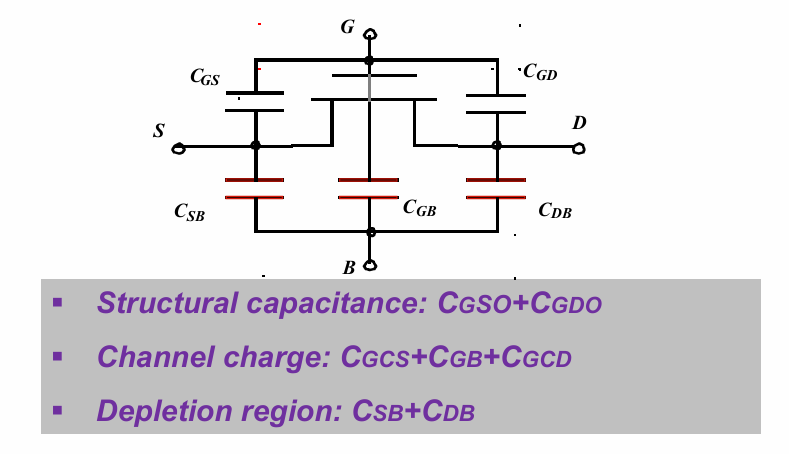
源-漏电阻

晶体管的电阻可能进一步受到源漏电阻的影响：

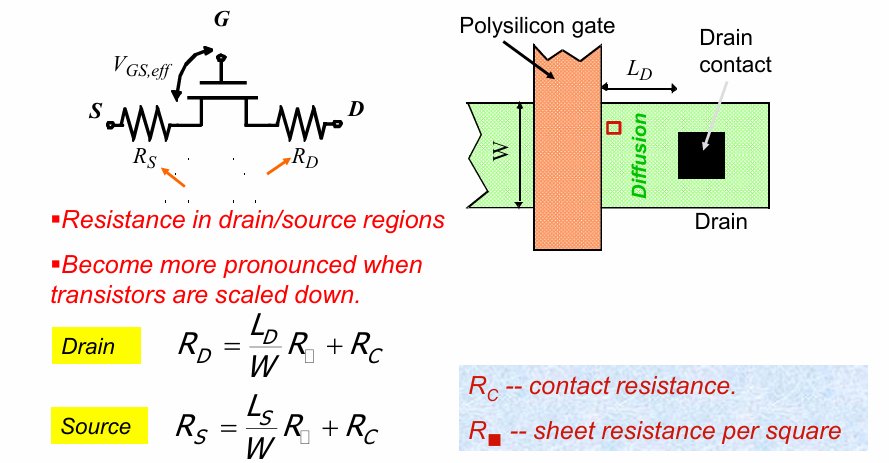
先进器件

略

Lecture3 Inverter

反相器是连接器件到电路的桥梁，因此对反相器的研究可以起到很好的承上启下的作用。

概述

电路

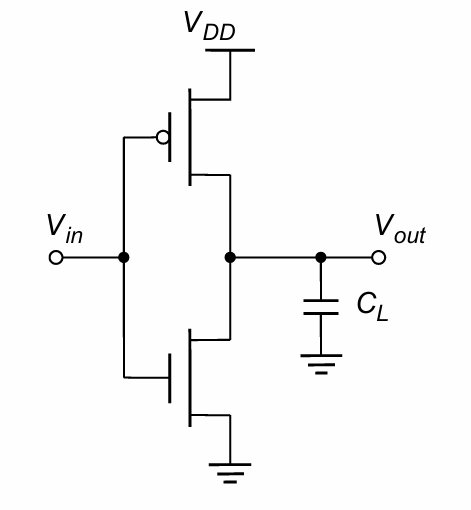
反相器的电路图如图所示。由gate 和drain端相连的一个PMOS和一个NMOS组成，当输入为高电平时，P管关闭而N管打开，VOUT为低电平。输入为低电平时则相反，N管打开而P管关闭，VOUT被拉高。

瞬态响应

反向器的瞬态响应，可以看作是通过P管和N管对于负责电阻$C_L$的充放电过程：

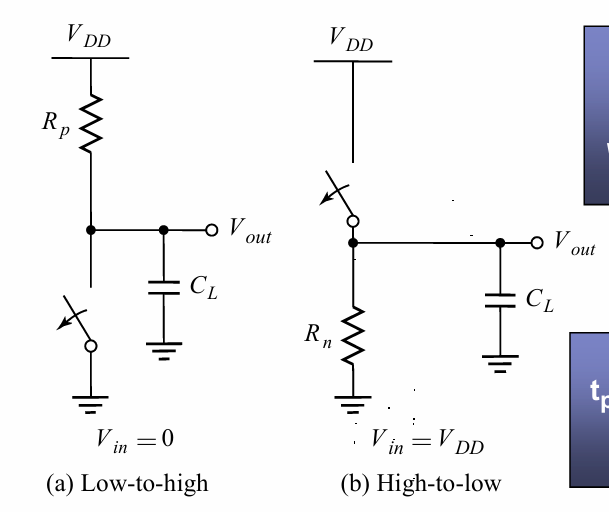
根据基本电路理论，其传输延迟为 $t_p= ln2 \cdot RC = 0.69R_{on}C_L$

传输特性曲线

反向器的传输特性曲线如下：

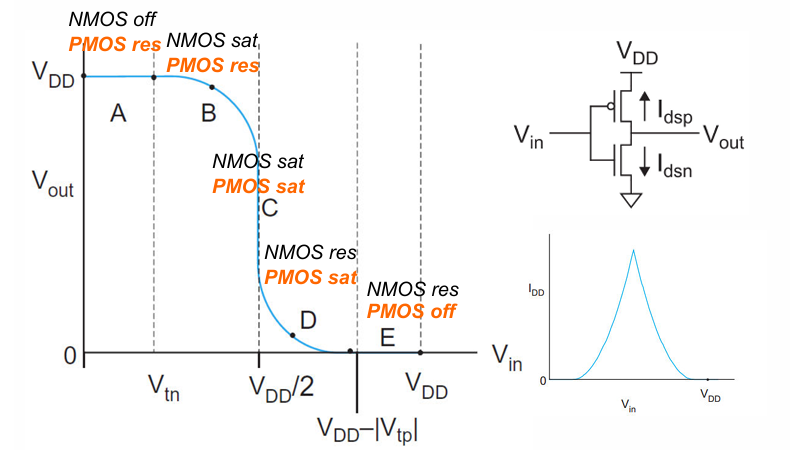
需要注意的是，在CMOS电路中，在稳定的工作状态下，不存在从VDD到VSS的直接电流，只有在状态翻转的过程中有一个瞬时的大电流。

翻转阈值

将反相器的翻转阈值定义为：
$$V_M = V_{in}=V_{out}$$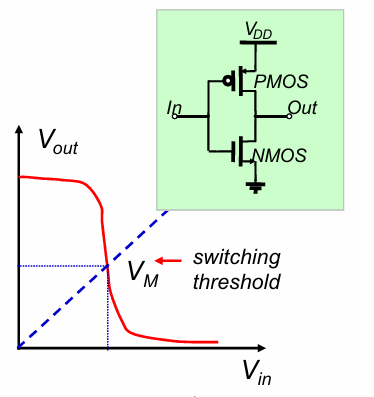

根据上述公式，在该点下，P管和N管均处于饱和状态($V_{ds}=V_{gs}$)，假设晶体管为短沟道器件，达到速度饱和，带入电流公式：

$$I_D = k’\frac{W}{L}((V_{GS}-V_T)V_{DSAT}-\frac{V_{DSAT}^2}{2})$$

可以解得：

当VDD的值相比晶体管的阈值电压和饱和电压相比足够大时，简化为“

$$V_M \simeq \frac{rV_{DD}}{1+r}$$

由于r 是一个与P N管宽度只比相关的参数，因此可以通过调节PN管的比值来调节$V_M$的大小：

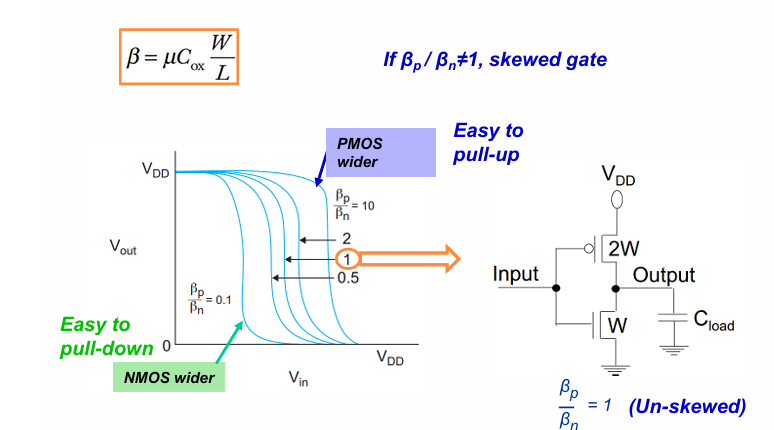
一般来讲，当$\frac{W_p}{W_n} = 2$时， $V_M$接近$V_{DD}$的一半。

$V_{IH}$,$V_{IL}$与噪声容限

对于反相器而言，将VTC曲线的斜率为-1(增益为-1)时Vin的值定义为$V_{IH}$,$V_{IL}$

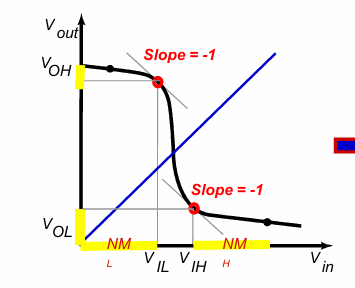
而数字设计中，往往采用线性分段近似的方式，通过求得$V_M$处曲线的斜率g,确定$V_{IH}$和$V_{IL}$：

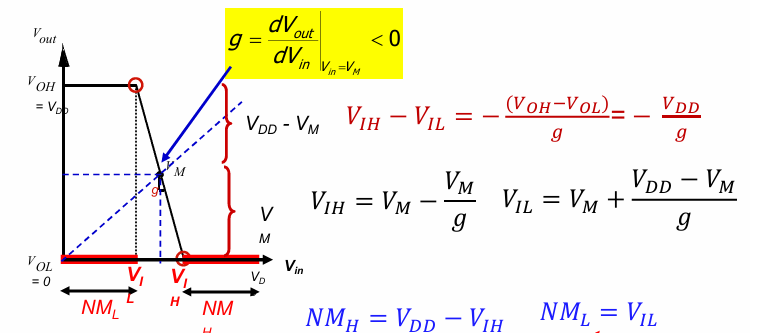
此时假设$V_{OL}=0$,$V_{OH}=V_{DD}$,计算得到相应的噪声容限。

传输增益

略

负载电容

接下来分析反相器的负载电容。假设2个反相器进行串联，分析其负载电容$C_L$：

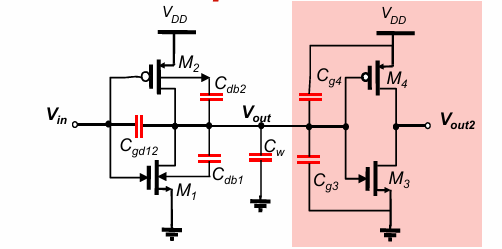
$C_L$的组成包括：

栅漏电容 $C_{gd}$

$C_{gd12}$指12这两个管子的栅与漏之间的电容，如之前在器件一栏分析的，该电容一方面由栅极的覆盖（栅氧化层）电容有关，另一方面与栅极电压感应出的沟道电容有关，即：

$$C_{gd} = C_{gdO} + C_{gcd}$$

其中栅氧化层电容$C_{gdO}$的值是固定的，而沟道电容$C_{gcd}$与晶体管的工作状态有关。对其进行分类讨论如下：

可见无论何种工作状态下，沟道电容均为0，故栅漏电容只等于覆盖电容：

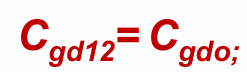
此外，需要考虑晶体管的米勒效应，将浮空电容用2倍的接地电容来替换，最终结合版图计算得到的栅漏电容$C_{gd1,2}$为：

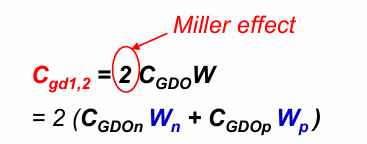
漏体电容$C_{db1}$和$C_{db2}$

漏体电容$C_{db1}$和$C_{db2}$来自漏体之间反向偏置的PN结形成的结电容，满足PN结的电容公式。为了简化计算，一般采用一些线性公式进行近似。

扇出的栅电容$C_g$

假设栅电容为扇出的栅上的总电容，有：

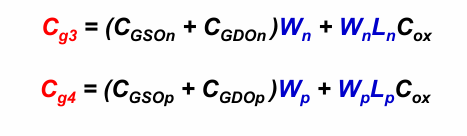
连线电容 $C_W$

$C_W$ 的值与具体工艺相关

将上述所有电容加和，便得到反相器的负载电容$C_L$

传输延迟

如前所述，对反相器的传输延迟的分析可以近似为一个一阶的RC模型：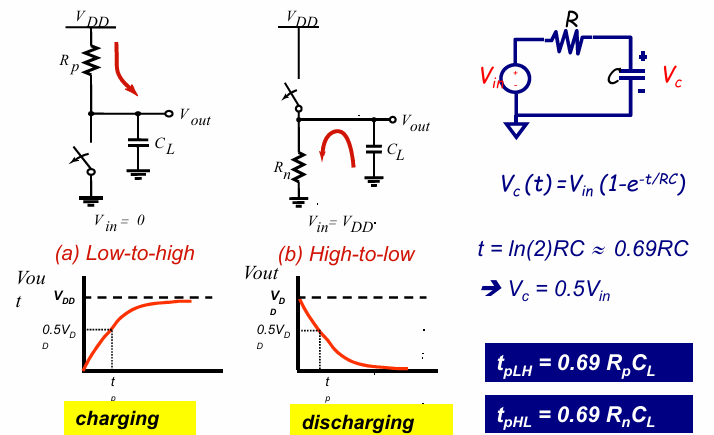

之前的分析已经计算出了反相器的负载电容，接下来需要考虑反相器工作时的等效电阻。

对等效电阻的分析如下：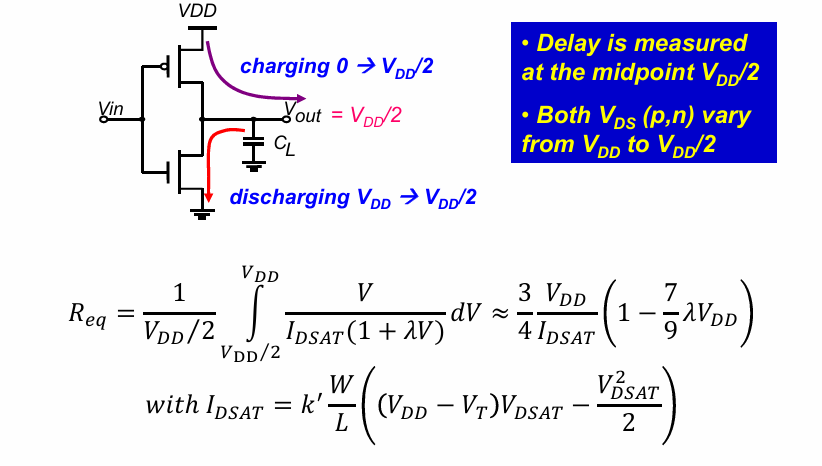

可以看到，正如前面强调过的，等效电阻是一个与电源电压VDD相关的参数，且与VDD负相关。

当计算传输延迟时：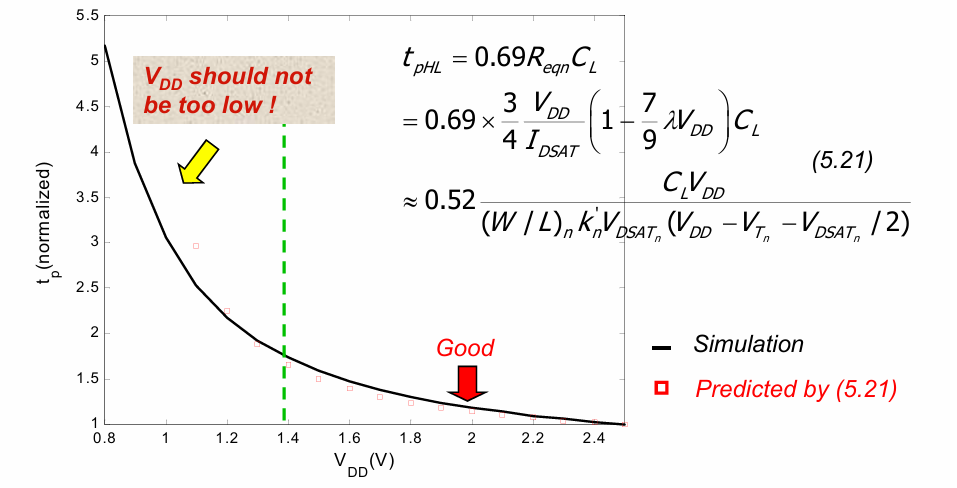

可以发现随着工作电压的提高，传输延迟也会下降，从而电路的性能提升。这也符号我们的一般直觉，即电压越高，对电路的”驱动”能力越强。

此外，传输延迟也与输入信号的变化有关：

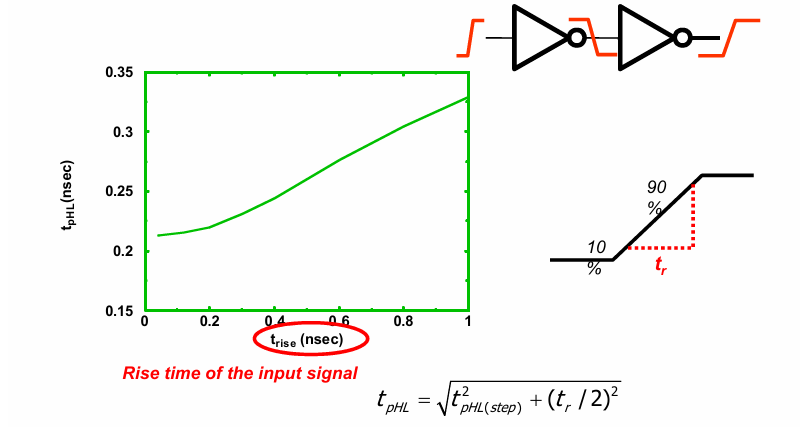
由于输入信号并非理想信号，其变化时间也需要被考虑在传输延迟之内。

晶体管尺寸比例的确定

在上一节中，为了是传输特性曲线VTC对称，得出P管和N管的比例系数$\beta$约为2。而对称的VTC并不意味着总延迟(high to low 和low to high之和)最小。

实际的实验结果如下：

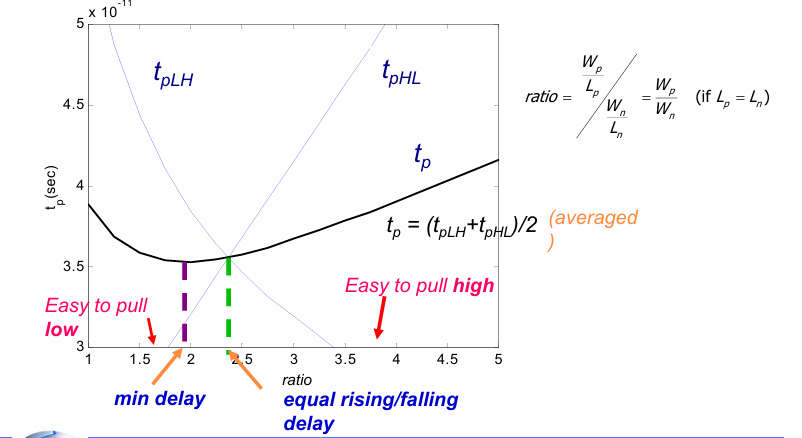
可以看到，相等上升和下降传输延迟(2.4)与总延迟最小(1.9)的比例系数并不相等。

好在它们都在2附近，于是$\beta=2$便成为默认比例系数。

sizing的影响

在上述分析中，我们总是假设晶体管的负载电容为$C_L$,然而事实上，$C_L$可以包含2个部分：本征电容$C_{int}$与外部电容$C_{ext}$。还是用之前2个反相器相连的例子：

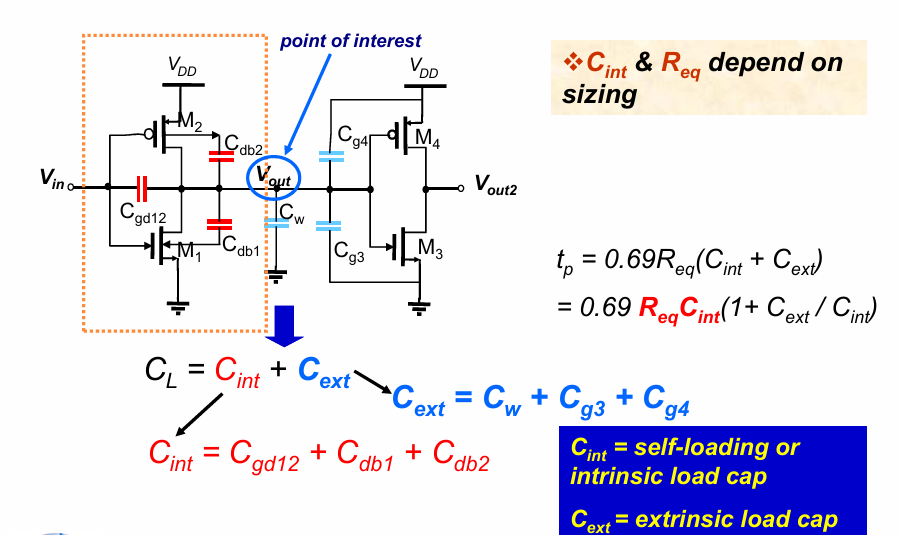
将$f = \frac{C_{ext}}{C_{int}}$称为等效扇出。

当反相器的尺寸整体扩大S倍时，其电容大致扩大为原来的S倍，而电阻却下降为原来的1/S,这使得延迟参数$R_{eq}C{int}$不变。而由于sizing增大了本征电容的值，使得$\frac{C_{ext}}{C_{int}}$变小，从而整体的传输延迟变小。

即：在外部负载电容不变的情况下，反相器的尺寸越大，其”驱动”能力越强，传输延迟越小。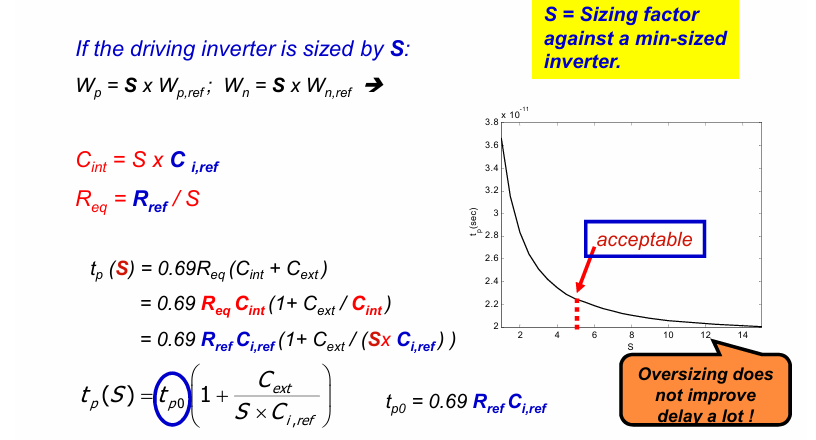

同时需要注意的是，由于延迟与sizing的系数成反比，随着S的增大，在延迟的收益上会逐渐减小，无法通过sizing的方式无限降低延迟。

* 对传输延迟的sizing优化

在对反相器的sizing有了基本认识后，可以考虑对传输延迟进行优化。

考虑如下图所示的一个反相器链(inverter chain)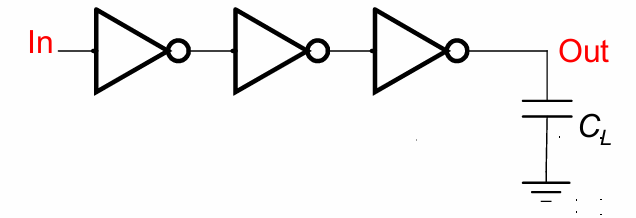

对于反相器链中间的任意一个inverter来说，其输出负载($C_{ext}$)是下一级反相器的栅电容$C_g$,而其自身的栅电容是上一级反相器的输出负载。

对于反相器而言，本征电容和栅电容成线性关系：
$$C_{int} = \gamma C_g$$
对于亚微米工艺，$\gamma \simeq 1$
于是对第j级有：

$$t_{p,j} = t_{p0}(1+\frac{C_{g,j+1}}{\gamma C_{g,j}})$$

考虑整个N级反相器链的传播延迟，有：
$$t_p =t_{p0} \sum_{j=1}^{N}(1+\frac{C_{g,j+1}}{\gamma C_{g,j}})$$

其中$C_{g,N+1} = C_L$

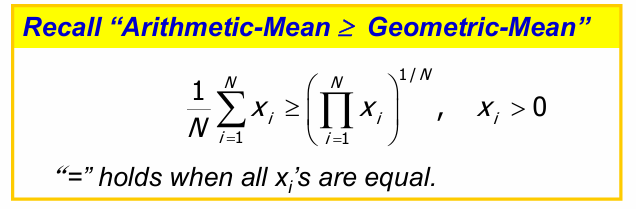
利用均值不等式求其最小值，可得：

$$\frac{C_{g,j}}{C_{g,j-1}} = \frac{C_{g,j+1}}{C_{g,j}}$$

即：每一级的反相器都相比前一级放到相同的倍数，记为f，满足：

$$F = f^n = \frac{C_L}{C_{g,1}}$$

$$t_p = Nt_{p0}(1+\frac{\sqrt[n]{F}}{\gamma})$$

对于一个级数不确定的反相器链，为了确定其最优传输级数，将上式对N求导(已知$\frac{\partial \sqrt[x]{y}}{\partial x} = -\frac{1}{x^2}\ln y \cdot \sqrt[x]{y}$)，另导数为0，可以得到：

$$f=e^{(1+\frac{\gamma}{f})}$$

上述超越方程只有一个解，当$\gamma = 1$时，f=3.6，解得：

$$N = \frac{lnF}{lnf}$$

功耗

CMOS电路的功耗分为2种：

动态功耗：逻辑状态进行翻转时的功耗

静态功耗：逻辑状态保持时的漏电流产生的功耗

CMOS反相器的功耗产生主要有以下几个方面：

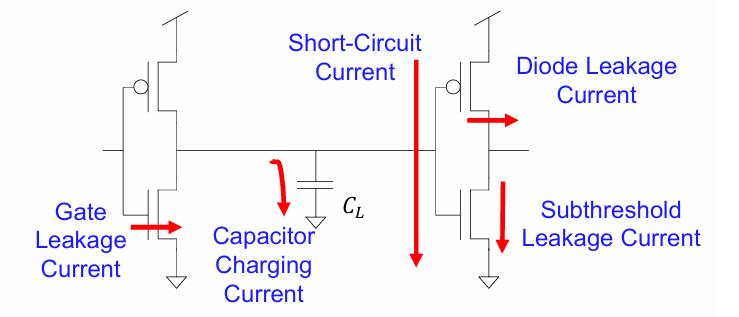
gate 端的漏电流
负载电容的充放电
进行翻转时的短路电流
漏极PN结的反偏电流
晶体管关断状态下的亚阈值漏电流

其中，主要的功耗来自逻辑翻转时产生的动态功耗。

动态功耗

当逻辑进行翻转时，PN两个管子同时导通，相当于产生了从VDD到VSS的短路电流。在上下其中一个管子关闭后，该电流需要对负载电容进行充放电，如下图：

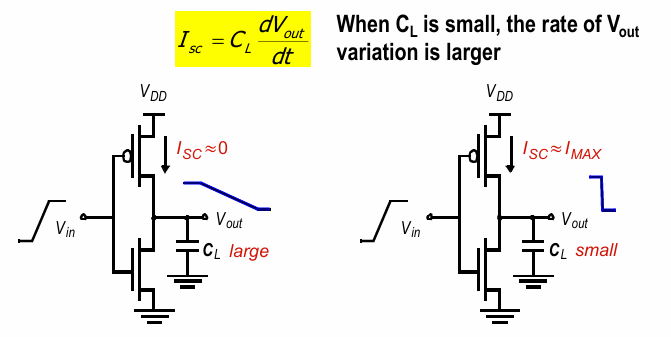
负载电容的大小会影响峰值电流的大小，具体来说，负载电容越小，峰值电流越大：

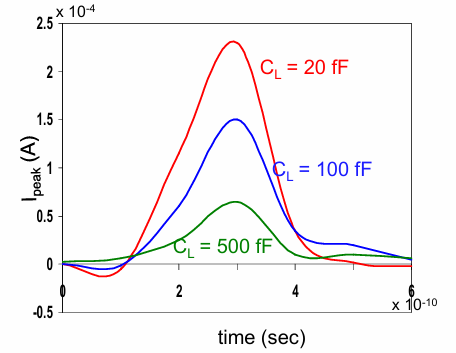
对于动态功耗的计算，每次从低到高翻转消耗的能量为：

$$E = C_LV_{dd}^2$$

其中$\frac{1}{2} C_LV_{dd}^2$的能量用于电容的充电，另外一半被PMOS或转化为热量，在放电时，另一半存储在电容的能量被NMOS转换为热量(这也是芯片放热的主要来源)。并且这个值与晶体管的尺寸无关，而只与负载电容和工作电压有关。

如果考虑电路的从0到1的翻转频率，则有：

$$P_{dyn} = C_LV^2_{DD}f_{0\rightarrow1}$$

针对最小功耗的反相器链sizing

上一节针对反相器链的性能进行了sizing,事实上，还可以针对最小功耗进行sizing。
(待补充)

PDP和EDP

如第一节中所定义的，反相器的PDP和EDP如下：

当需要平衡功耗与性能，使反相器的EDP最小时，我们假设书中的公式5.21：

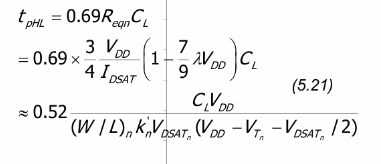
其中阈值电压和饱和电压满足一定的比例关系，可得：

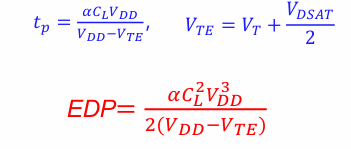
另上述EDP对VDD的偏导为0，得：

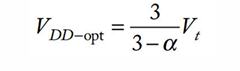
对于一般的亚微米工艺，$\alpha$在1到2之间。

Lecture4 Combinational Circuits

本章将介绍组合逻辑电路，分为以下几个方面：

静态/动态CMOS 逻辑
组合逻辑门
不同输入下的门延迟
快速逻辑门设计
逻辑努力与延迟优化
有比逻辑
传输管逻辑
动态逻辑

所谓组合逻辑，自然是与时序逻辑向对比而言的。二者的区别从抽象的角度来说，组合逻辑是输入的函数，而时序逻辑既是输入的函数，也是当前状态的函数。

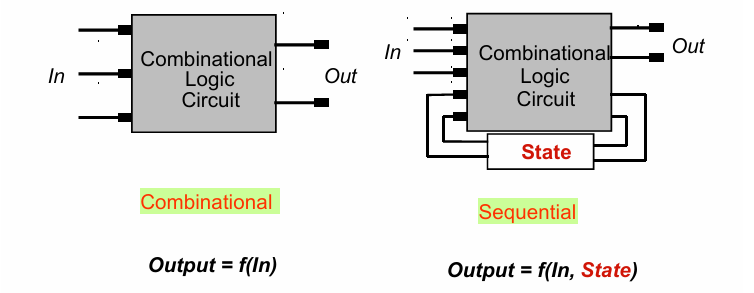
静态/动态CMOS电路

静态CMOS电路直接与电源和地相连，当电路稳定后，输出与时间无关。

动态CMOS电路则需要时钟信号控制。

组合CMOS逻辑门

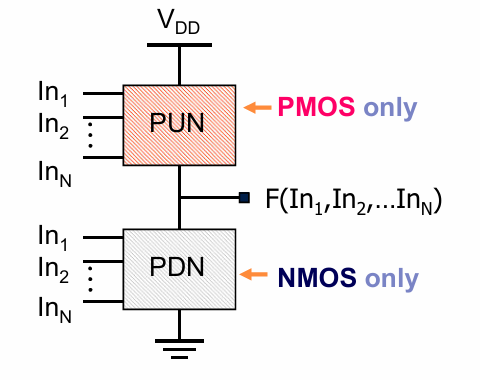
CMOS逻辑门分为上拉和下拉网络，并且上拉网络的拓扑结构与下拉网络的结构是对偶的。上拉网络完全由PMOS组成，下拉网络完全由NMOS组成。并且这样实现的逻辑总是PDN的非逻辑。

一个典型的例子是NAND门：

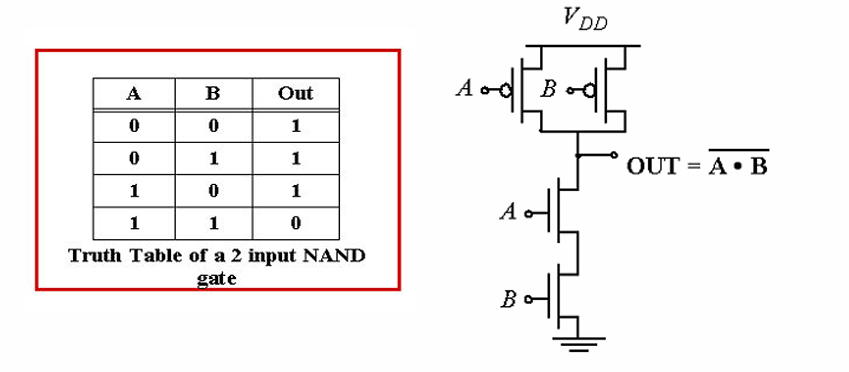
CMOS逻辑的优点在于：

逻辑摆幅大：CMOS集成电路的逻辑高电平“1”、逻辑低电平“0”分别接近于电源高电位VDD及电源低电位VSS，因此具有较高的噪声容限。也就是说，逻辑值的电平与管子尺寸无关。
具有低功耗特性：CMOS逻辑电路在静态状态下几乎没有功耗，只有在开关转换时才消耗功率。
可以通过sizing调节上升和下降的传输延迟

不同输入pattern下的传输延迟

CMOS组合逻辑仍然可以套用之前的RC模型:

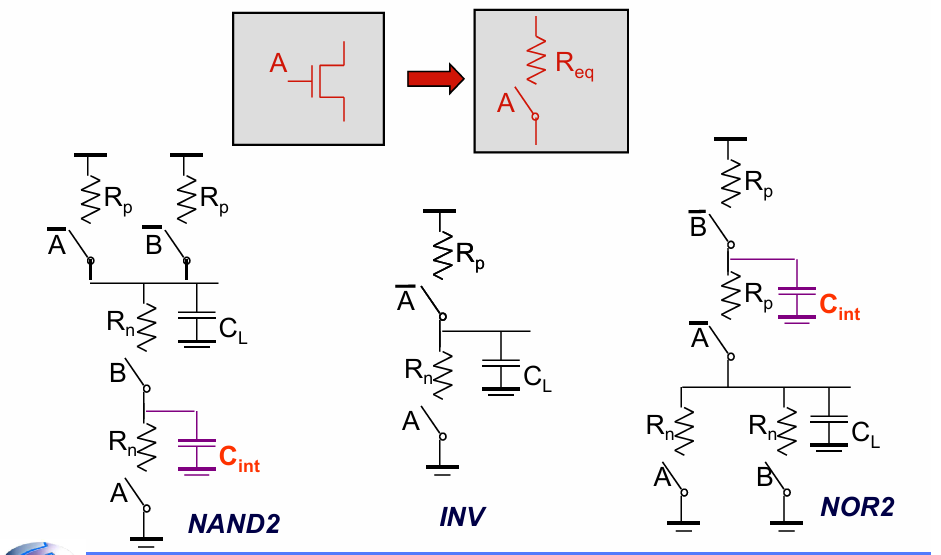
与反相器不同的是，不同的输入组合会使传输延迟有所不同。例如考虑一个NAND门：

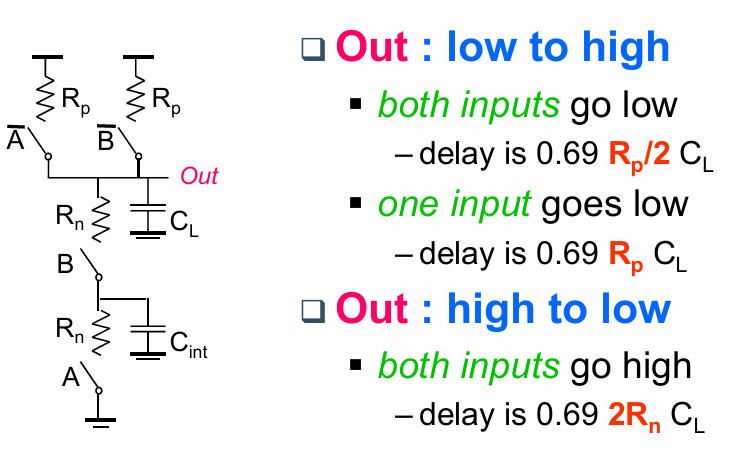
当输入AB同时拉低时，通过2条并行的线路同时对负载电容充电，从而传输延迟相比只有一条通路时有所下降。

还有一种最坏的情况为： B保持为1，A由1变为0，这个过程中，不但要通过A所在通路向负载电容充电，同时也需要对中间节点的电容充电：

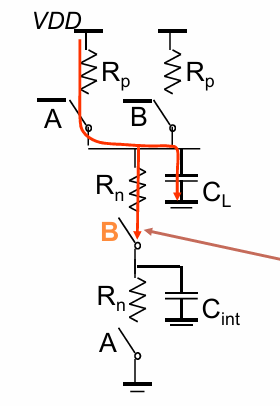
逻辑门的sizing

之前的章节我们分析过，对于晶体管，其尺寸(主要是宽度W)每扩大S倍，其等效电阻降低为原来的1/S。

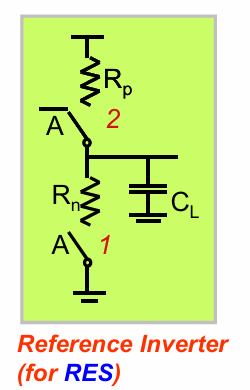
对逻辑门sizing的初衷在于，想要使上拉和下拉的传输延迟与一个标准的CMOS反相器(PMOS尺寸为NMOS的2倍)相同。而对一个逻辑门，总是考虑其最坏情况下的传输延迟。

因此sizing的逻辑在于将串联的管子尺寸翻倍，以使其等效电阻与单个单倍尺寸的管子相同

sizing过后的NAND和NOR门分别如下：

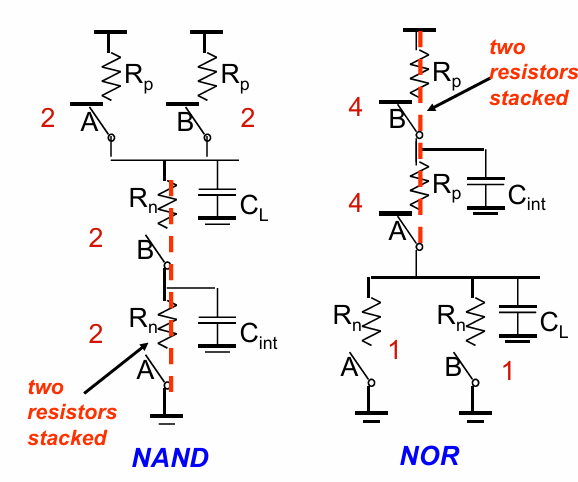
对扇入的考量

当逻辑门的输入增多时，逻辑门的扇入也会影响逻辑门的性能，需要被纳入考虑。比如如下图所示的4输入NAND门：

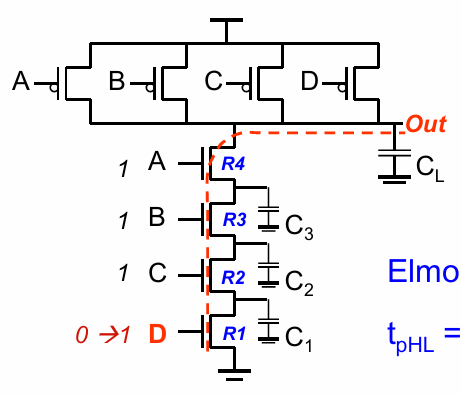
当ABC均为1，D从0变为1时，由于一开始OUT为高电平，$C_L$和内部节点$C_1,C_2,C_3$均被充电。

在放电过程中，电路的延迟可被计算为：

$$t_{pHL} = 0.69(C_L(R_1+R_2+R_3+R_4)+ C_3(R_1+R_2+R_3)+C_2(R_1+R_2)+C_1R_1)$$

当N管尺寸相同时，可以认为它们拥有相同等效电阻，于是延迟转化为：

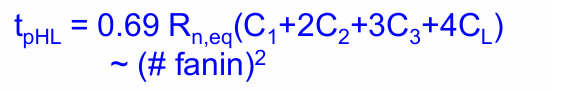
也就是说，逻辑门的延迟和扇入的数量成平方关系。因此大扇入对门的性能影响很大。

相比之下，扇出对延迟的影响是线性的。

快速逻辑门设计

基于上述对fin-in的考察，对于一个同样功能的逻辑门，有以下不同方式可以降低其延迟：

递进式sizing

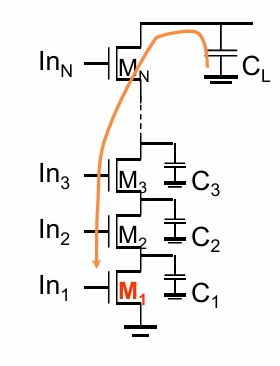
对于类似的串联结构，由于M1管的电阻对整体延迟贡献的最多，因此可以将其尺寸适当放大以减小电阻。同样我们可以逐级放大后续管子的尺寸，使得：

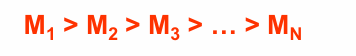
这样的sizing方式可以降低大约20%延迟。

晶体管的重排

通过重排，将先翻转的逻辑门从近输出端移到近地端，让内部电容提前放电，可以有效降低延迟：

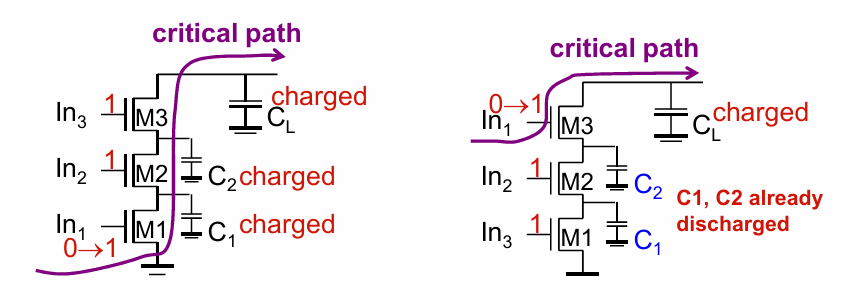
逻辑重构

对于同一逻辑，使用不同的门进行组合可以降低其延迟。

例如对一个8输入与门有以下几种不同的实现方式：

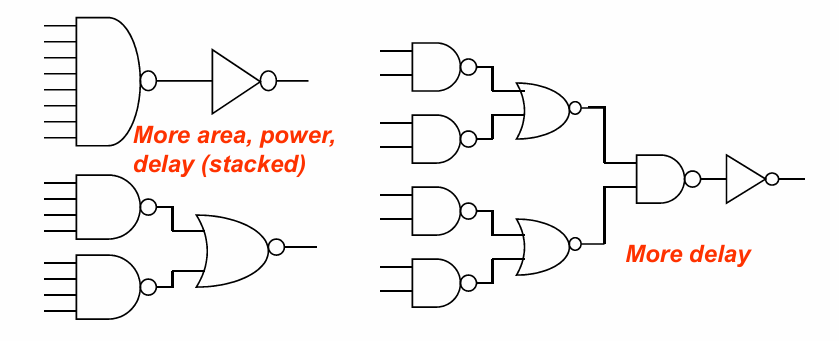
插入buffer增强驱动

这样做能够增强驱动的原理在于，buffer的加入将fan-in和fan-out进行了隔离。

逻辑努力

先前对反相器链的分析中，我们知道通过对一整个链上的反相器进行sizing，可以有效降低整个路径的传输延迟。通过引入逻辑努力，可以将上述分析方法推广到所有组合逻辑门。

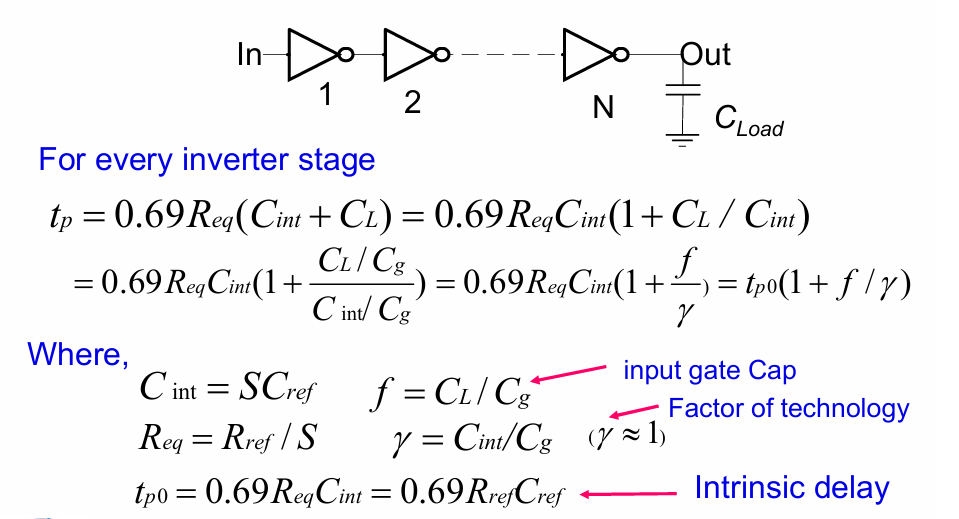
首先回顾反相器链的知识，一个标准反相器的延迟可以被表示为：

$$t_p = 1+\frac{f}{\gamma}$$

其中f为等效扇出，$\gamma$是工艺参数，代表本征电容和栅电容的比值。

$$C_{inv} =\gamma C_{g}$$

将上述分析方式推广任意逻辑门：

注意上述推导过程，在第三行中，提取一个标准反相器的本征电容$C_{int}$作为公因子，在第五行中将这个值代换成了标准反相器的栅电容$\gamma C_{ginv}$。同时，假设通过sizing使标准逻辑门拥有与反相器相同的电阻，从而$R_{par} = R_{inv}$。

第四行的$C_g$是逻辑门的栅电容。

最终我们得到公式：

$$t_p = t_{p0}(p+ \frac{g\cdot f}{\gamma})$$

其中：

$p$是逻辑门本征电容和标准反相器本征电容只比，这个值只与逻辑门的类型和拓扑结构有关。

例如，对一个n输入的nand门，其p值为n:

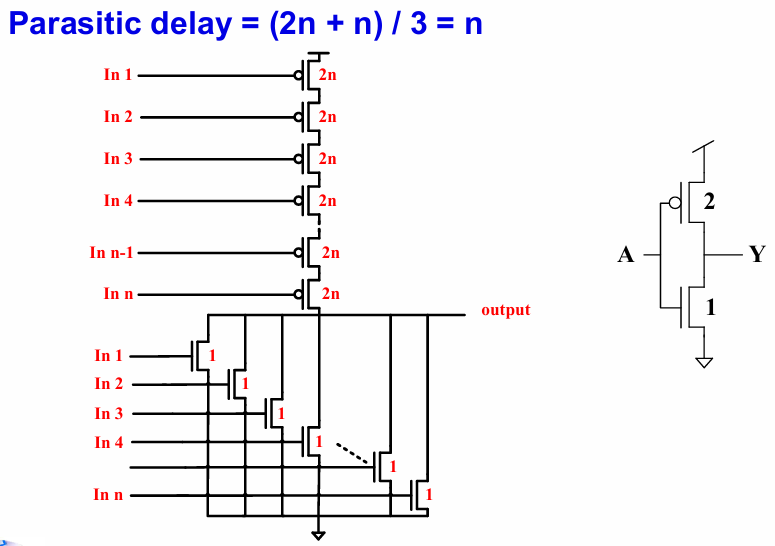
而对于下面的异或门，其p值为4：

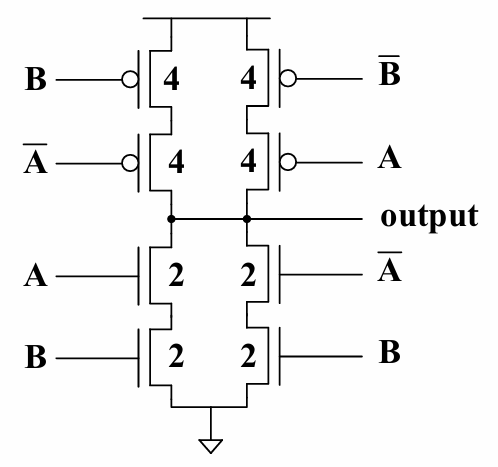
（计算方法是看其对输出节点贡献的负载电阻。）

不同逻辑门的p值总结如下：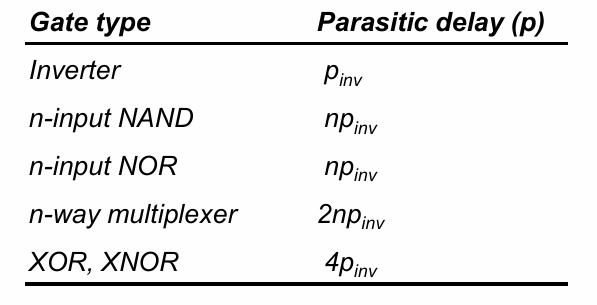

$g$称为逻辑努力，是门输入栅电容与标准反相器栅电容的比值，与逻辑门的类型有关。下表总结了不同类型的逻辑门的逻辑努力：
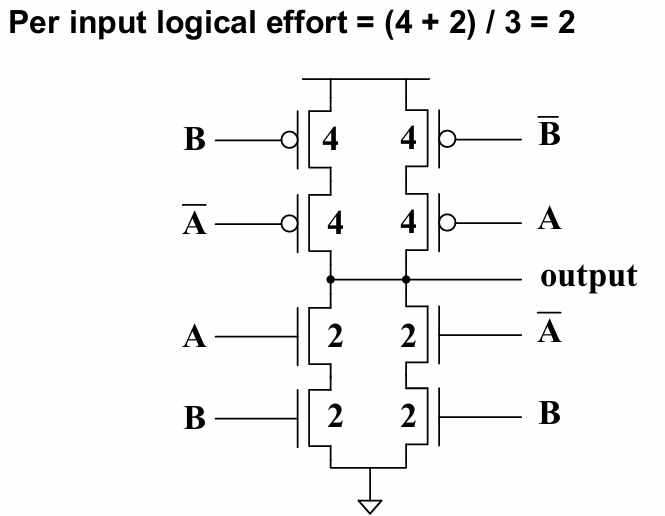
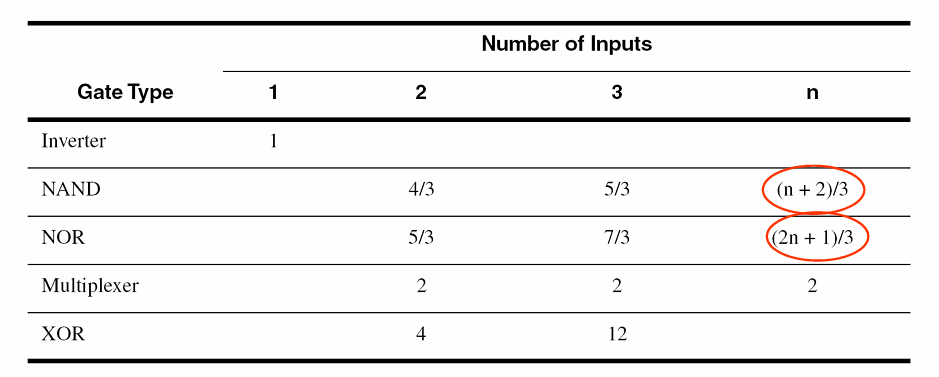
$f$为等效扇出，与反相器链中定义的一致，只不过这里的扇入是逻辑门的栅电容。

非对称逻辑门 skewed gates

(待补充)

分支努力

假设同一个逻辑门的扇出路径上存在多个相同的逻辑门，如下图所示：

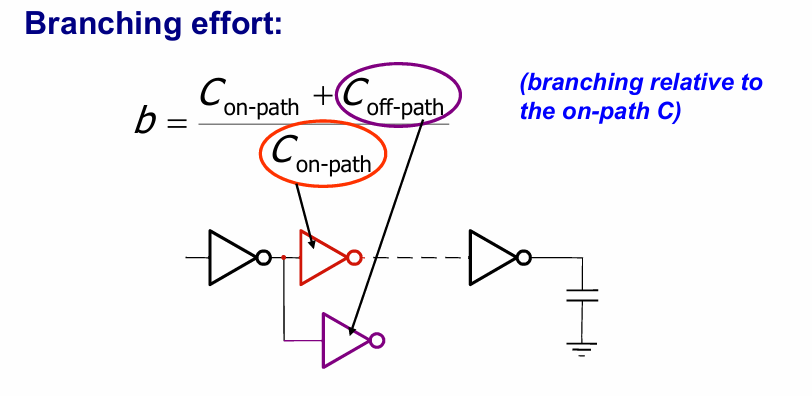
假设逻辑门共有b个分支，则对于单个逻辑门，其外部负载变为原来的b倍，传输延迟变为：

$$t_p = t_{p0}(p+ \frac{g\cdot f\cdot b}{\gamma})$$

考虑一个多级，多分支的路径，其总延迟为：

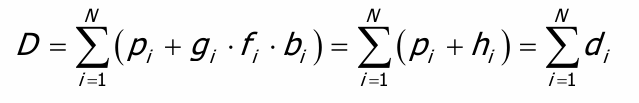
优化上述延迟，使总延迟最小：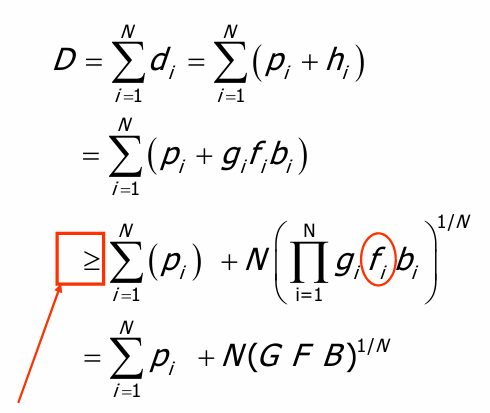

当且仅当每一级的

$$h_i = g_if_ib_i$$

都相等时，整个链路的延迟最小。

而对于每一级来说，逻辑努力g和分支努力d都是固定的，能够进行sizing的参数只有f。

当电路的级数固定时，令每一级的级努力h都相等，可以取得最低延迟。

example

例：优化下面电路的延迟：

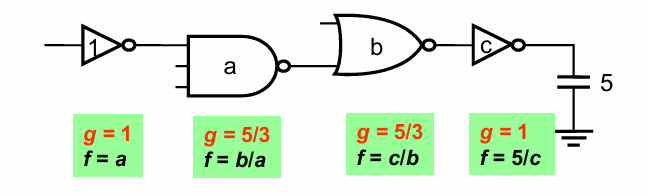
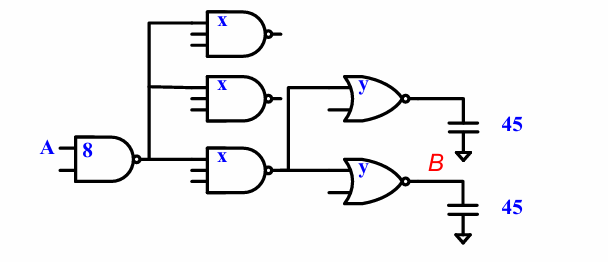
总结

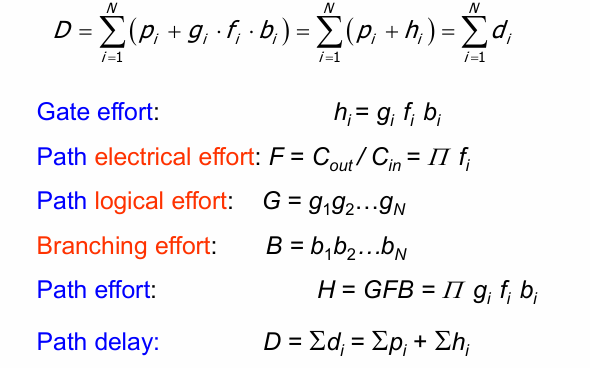
Ratioed Logic 有比逻辑

除CMOS逻辑外，对同一电路功能还有其他实现方法，比如有比逻辑。

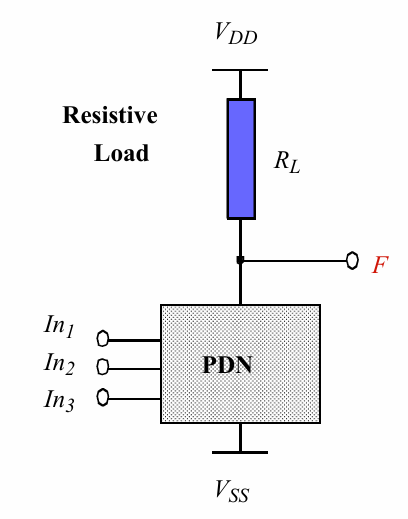
有比逻辑将CMOS中的上拉网络用一个电阻负载进行替代，可以有效减小电路的面积。有比逻辑具有以下特点：

n输入的逻辑由n个管子和一个负载组成
$V_{OH} = V_{DD}$
$V_{OL}=\frac{R_{PN}}{R_{PN}+R_{L}}V_{DD}$
具有非对称的响应时间
静态功耗很高
$t_{pLH}=0.69R_LC_L$

伪nmos逻辑

上述有比逻辑在实际实现时，可以通过一个敞开的PMOS来代替电阻：

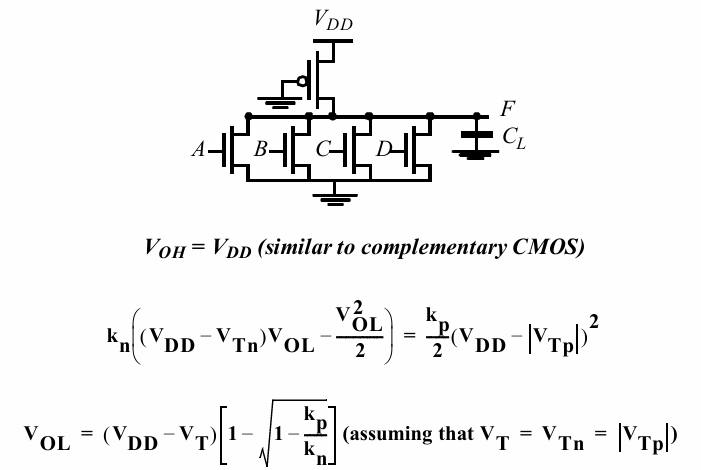
这样实现的问题是$V_{OL}$不为0，且与P管与N管的尺寸比例有关(所以叫有比逻辑)。当P管的驱动能力太强时，下拉的N管可能不足以将电路拉低：

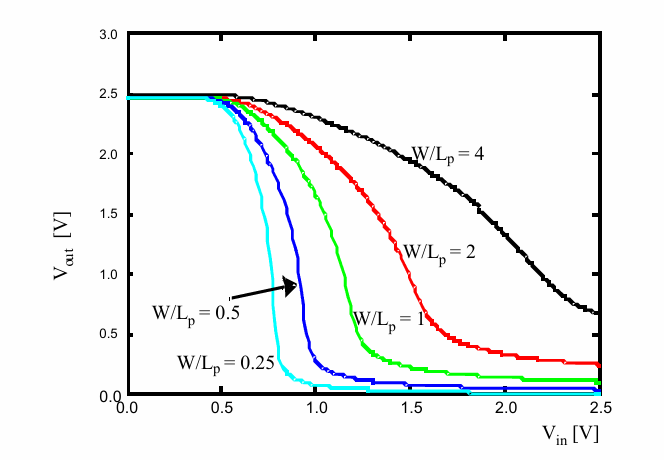
有比逻辑的优化

基于有比逻辑的缺点，可以对其进行一些改进

改进负载

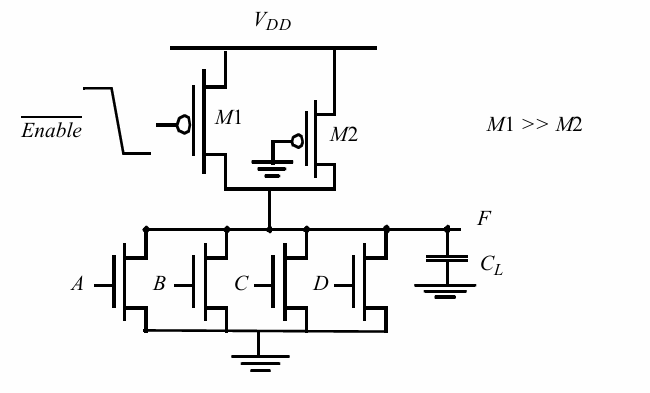
添加一个enable负载，增强P管驱动

差分级联电压开关逻辑 Differential Cascode Voltage Switch Logic (DCVSL)

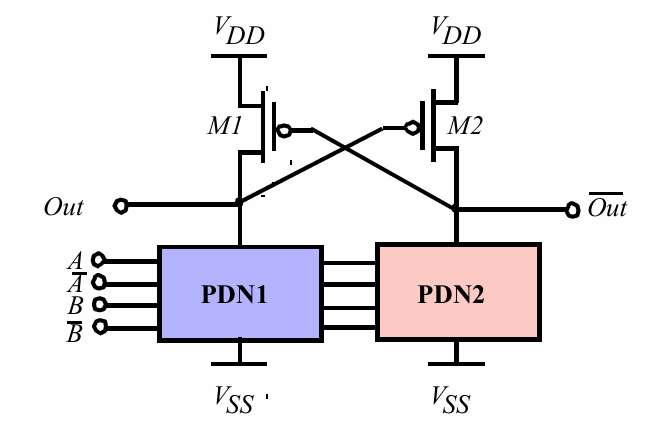
将2个下拉网络的输出端进行级联，并且下拉网络彼此对偶。当一个电路打开时，另一个一定关断。例如下面的与门：

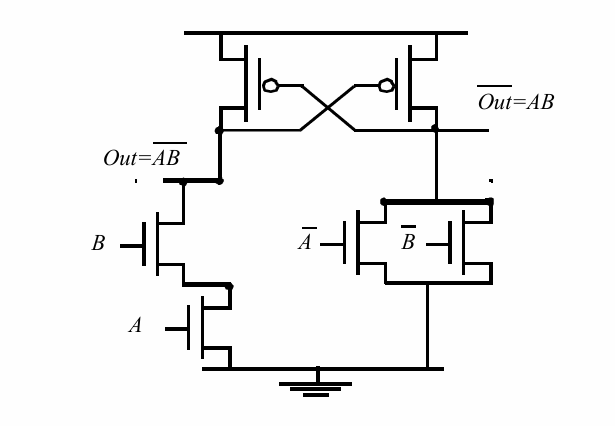
差分逻辑具有如下特点：

全电压摆幅。($V_{OL}$=0，因为out为0会反馈回来关掉上拉网络)。
无静态功耗
2个互补的输出直接没有延迟

传输管逻辑

在一般的晶体管电路中，输入都被送到晶体管的栅极，而在传输管逻辑中，输入被送到晶体管的源/漏极，这样的好处是可以在功耗，面积或性能上得到提升。

nmos开关

当nmos作为开关时，存在的问题在于不会获得全摆幅的电压输出，如下图：

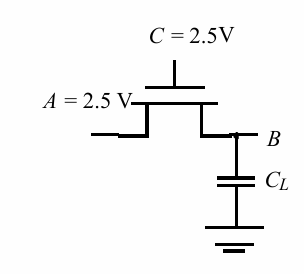
分析B点的电压，由于晶体管必须保持开启状态，有：

$$V_{GS}=V_C-V_B \geq V_t$$

B点的电压最多只能达到 $V_{DD}-V_T$

这为传输管逻辑的级联带来了问题：

如图：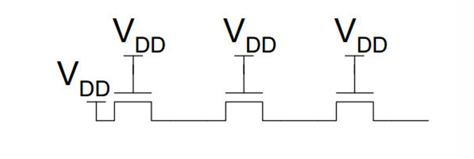

这样的连接方法在末端会损失一个$V_t$的电压。

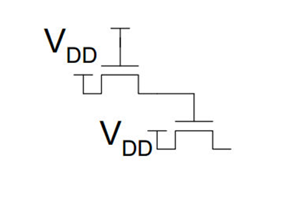
这样的连法没连接一次就会损失一个$V_t$的电压。

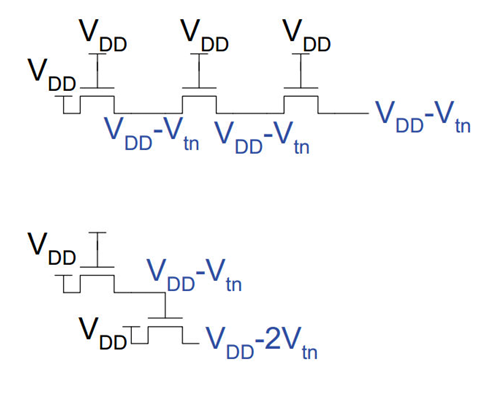
改进：level restoring

可以通过下面的方式改进输出不足的问题：

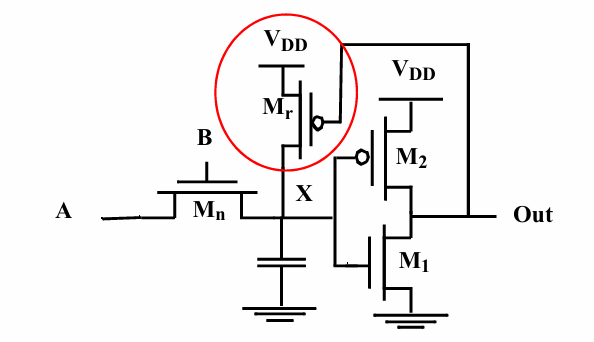
通过一个反馈的P管，将X点电压重新拉回VDD。问题在于，这样的电路是一个有比逻辑，$M_r$的尺寸不能太大，否则X点电压可能没办法被拉回0.

传输门逻辑

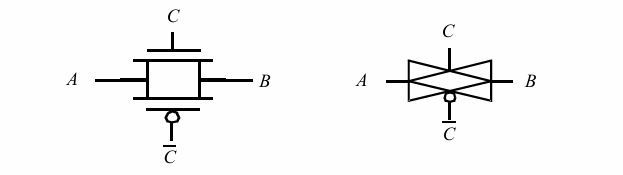
通过同时使用PN2个管子，得到一个全摆幅的输出

延迟分析

一个打开的传输门可以看作一个电阻，多级的传输门逻辑相当于一个RC网络，其延迟是级数的二阶函数：

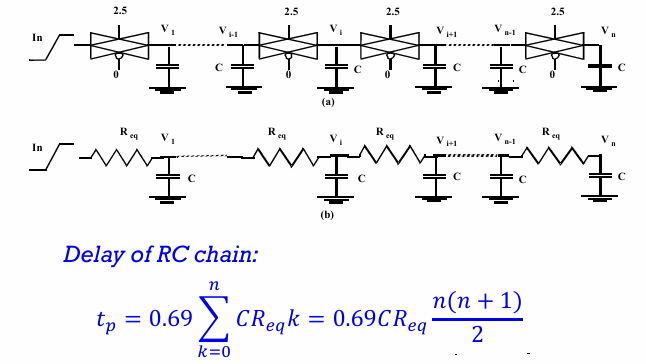
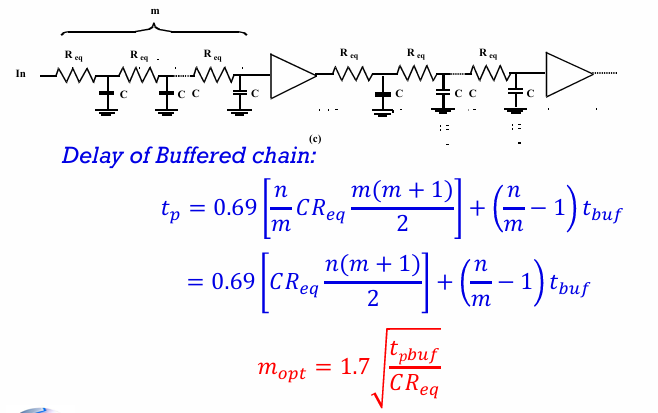
同样可以通过插入buffer的方式来降低延迟：

动态逻辑

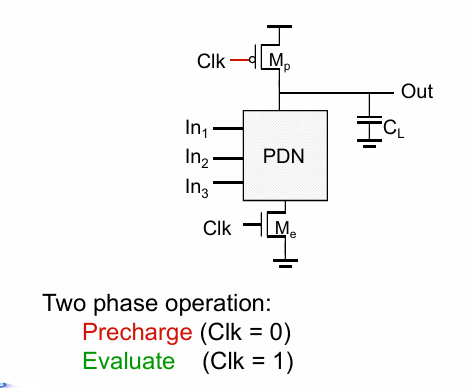
动态逻辑的电路结构如图，通过为PDN加上2个由clk信号控制的管子和一个下拉网络实现，一个n输入的逻辑门需要n+2个管子实现。

当clk为0时，最下方的n管关闭，上方的n管先对负载进行预充电。clk拉高后，充电结束，下方的n管打开，经PDN的计算决定要不要对负载进行放电。

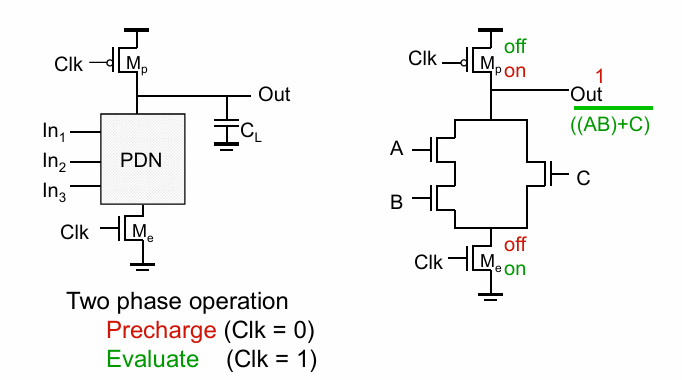
动态逻辑具有如下优点：

只用下拉网络进行计算(节约面积)
全摆幅输出
无比逻辑
翻转速度更快(相比CMOS，输入和输出负载都更小)

动态逻辑的缺点在于：

功耗一般高于CMOS逻辑。(每次预充电后计算，都可能放电，导致电路的翻转频率高于CMOS)

噪声容限较低。

漏电问题

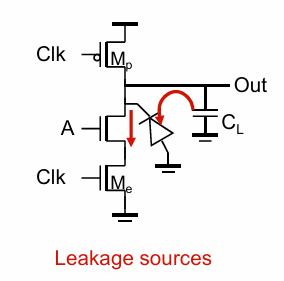
如下图，预充电后，A管的源极电压为高，S和B直接存在一个反偏的PN结，存在漏电流。这会导致$C_L$上的电荷减少，当进行计算时，无法得到一个满”1”:

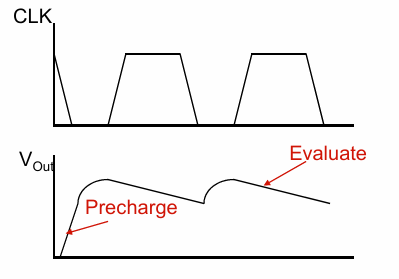
解决方案是通过一个反馈来进行电压维持：

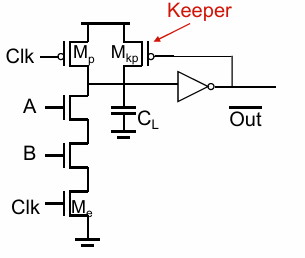
电荷共享问题

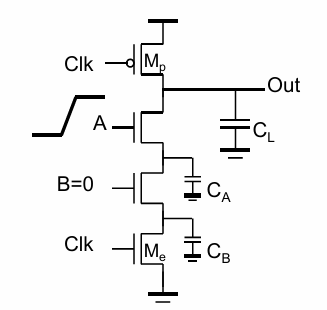
如果在clk为0，进行计算的时候，A由低变高，则$C_A$分担了$C_L$上的电荷，同样导致输出不能达到满”1”：

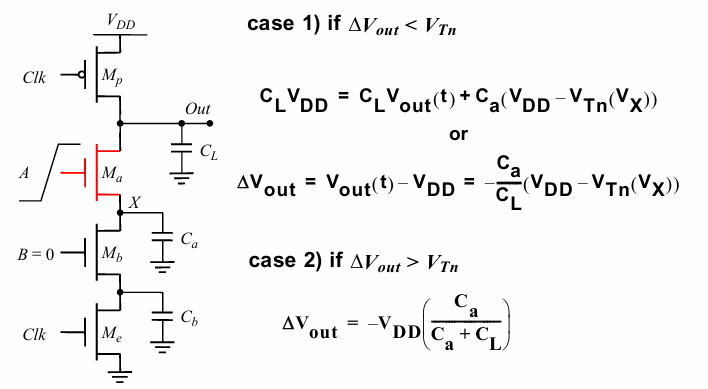
解决方案是使用clk控制的晶体管对中间节点进行充电：

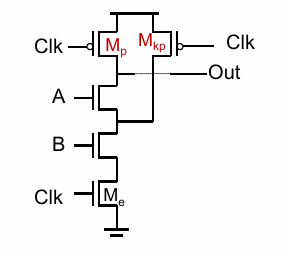
回栅问题 (back gating)

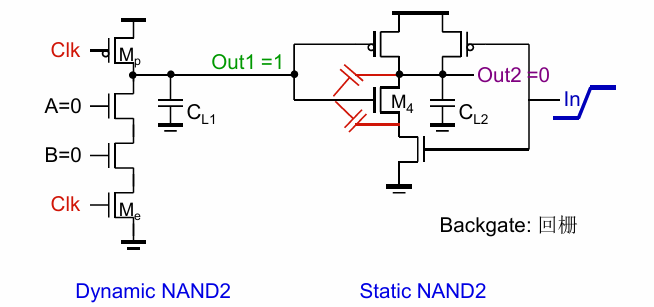
简单来说就是输入(out1)通过电容耦合到了输出(out2)上，使输出不能得到完全的计算。

时钟馈通 (clock feed through)

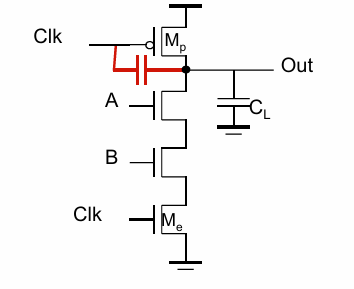
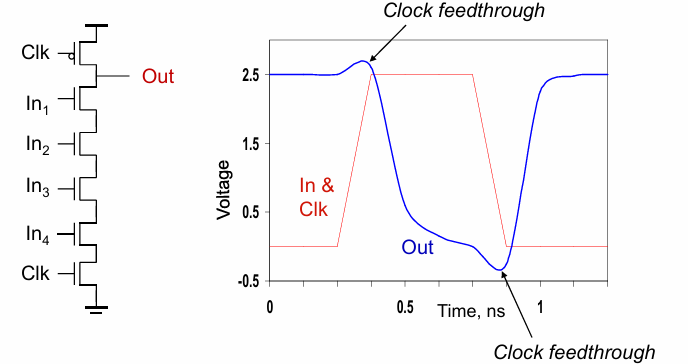
时钟信号的波动耦合到输出，使得输出峰值大于$V_{DD}$.

级联问题

如果将动态逻辑进行级联，同样会遇到输出下降的问题：

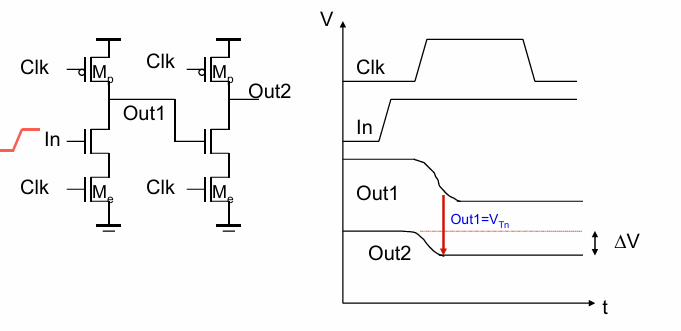
如图是2个串联的动态反相器，一开始clk为低时，out1和out2都被预充为1，在clk拉高后，它们分别开始计算。

由于in=1,因此out1的预期结果应该为0，而out2的结果应该为1.在计算过程中，out1节点会逐渐放电到0，由于out1降到0需要一定时间，在这器件out1控制的nmos仍然是打开的，因此out2也会通过下拉通路放电，知道out1的值降到vt以下才会结束这个过程。

通过上述分析我们可以发现，这种过程只出现在计算时不需要放电，但却因为输入是从1到0渐变的，导致了一部分电荷损失。如果输入是由0到1的，也就是说本来就需要对输出节点进行放电，则不存在这个问题。

因此可以通过增加一级反相器解决这个问题：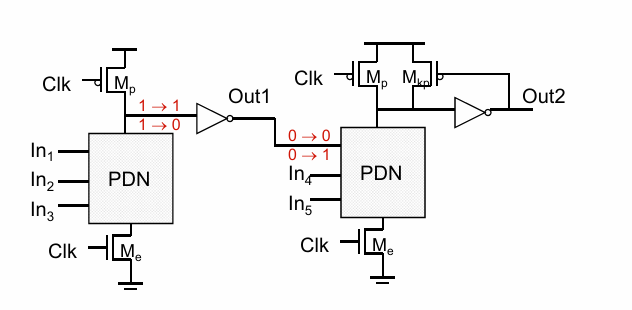

由于out1前面的节点总是被预充到1，out1自己总是被预放电到0，如果计算出out1=1,再对后面的节点进行放电，就不会有问题。

这样的多个动态逻辑的串联被称为多米诺逻辑：

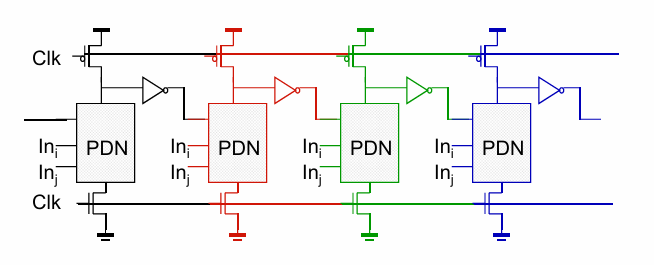
此外可以在多米诺逻辑的基础上省略下面的管设计出footless的多米诺：

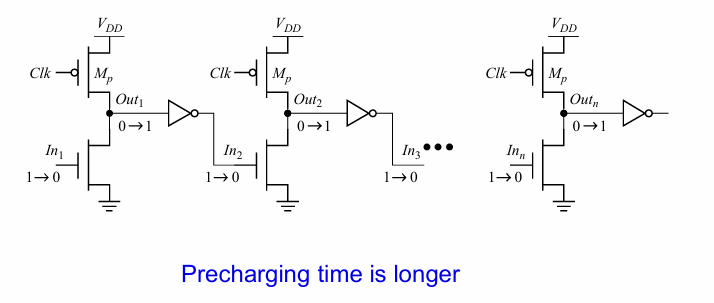
以及省略中间的反相器，做成np-CMOS：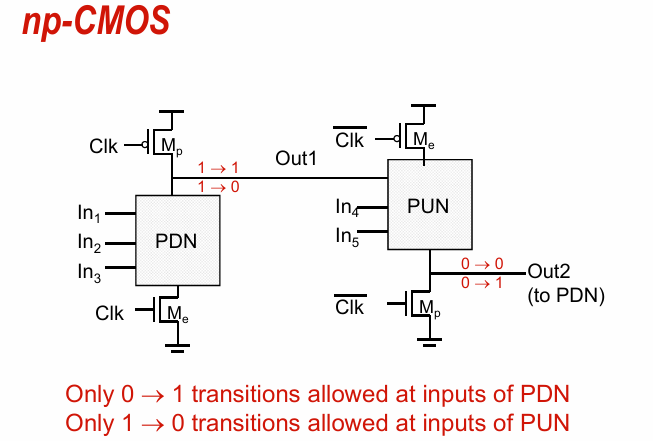

Lecture5 时序逻辑

时序逻辑与组合逻辑的最大区别在于，电路的输出不止由输入决定，也由电路当前的状态决定。

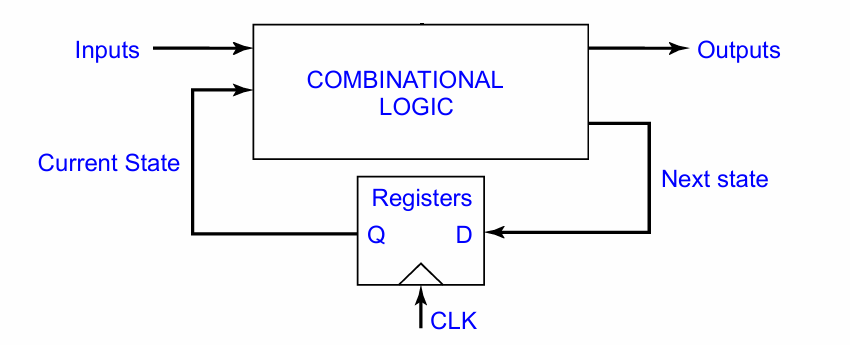
锁存器(latch)和寄存器(register)

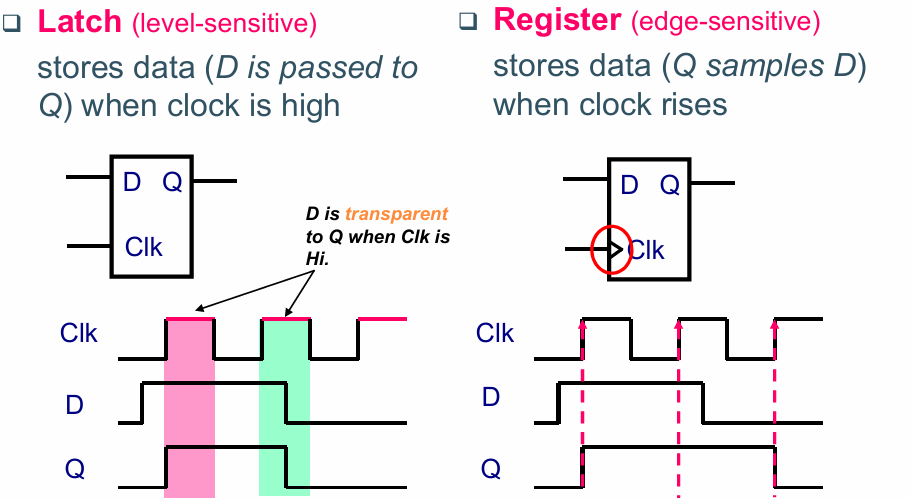
区别在于，latch在整个时钟拉高的阶段都进行计算，register只在时钟上升沿发生变化。

时序参数

对寄存器来说，有以下几个重要的时序参数：

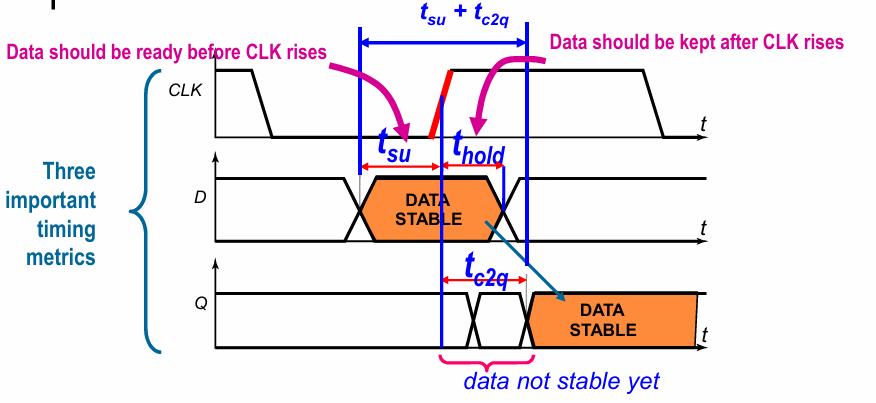
set up time: 时钟到来之前，数据需要提前准备好的时间
hold time：时钟到来之后，数据需要保持不变的时间
$t_{c2q}$:顾名思义，指时钟开始发生变化，到数据完成计算保持稳定的时间。可以看作是clk到q的传播延迟。

接下来定义如下参数：

传播延迟

污染延迟指输入信号开始变化后，输出信号完成变化的时间。也就是说，在传播延迟之后，数据才运算结束。

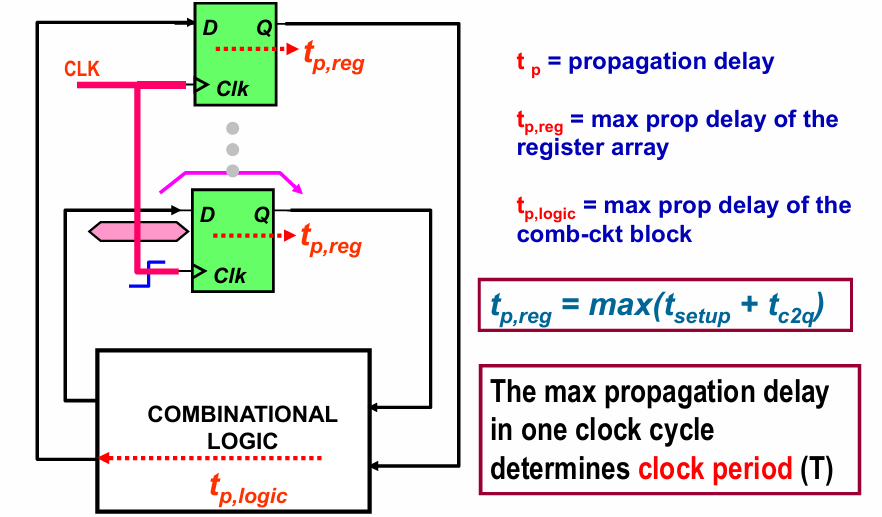
在这里要注意的是，传输延迟和数据端D无关，而是与时钟信号clk有关。

而$t_{p,reg}$不止需要经过寄存器的c to q传播，还需要数据提前准备好，所以要加上set up time。在传输延迟之后，数据不会有新的变化(一周期之内)

传播延迟决定时钟周期。

污染延迟

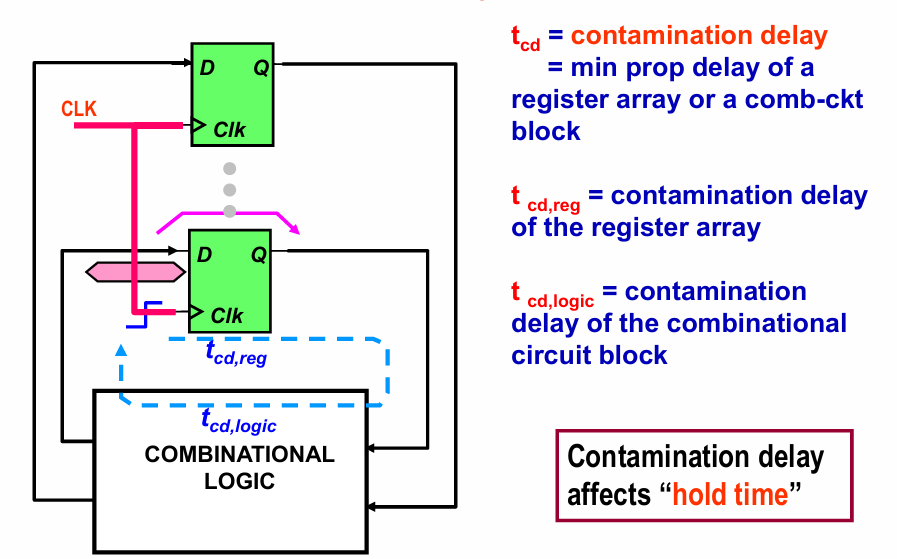
污染延迟指输入信号开始变化后，输出信号开始变化的时间。也就是说，在污染延迟之内，数据未发生任何变化。因此污染延迟被用来计算保持时间。

建立时间

对于一个流水线结构，时钟周期满足如下关系：

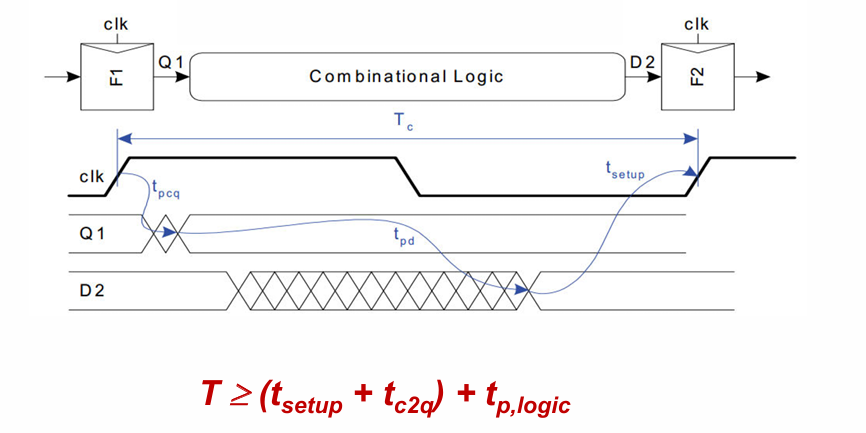
保持时间

对于一个有限状态系统，保持时间满足如下关系：

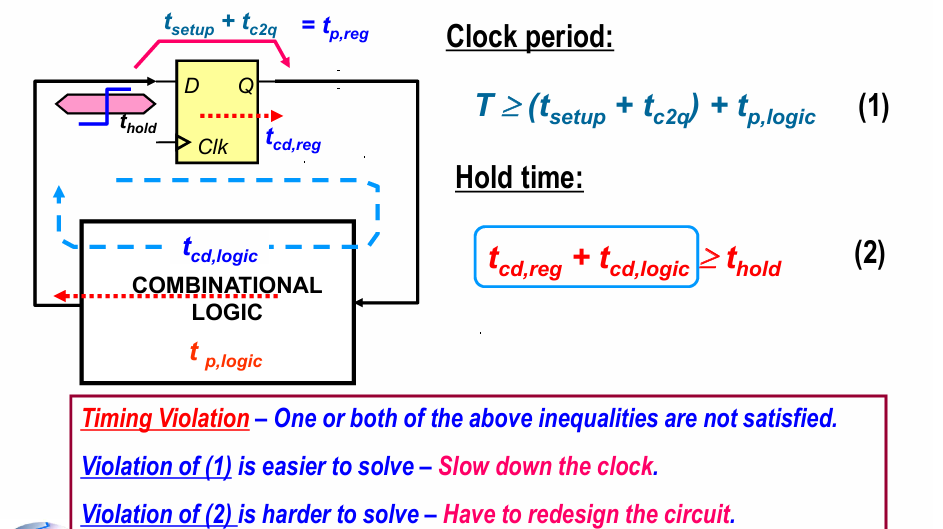
如果电路不满足建立时间，可以适当降频增大时钟周期，如果电路不满足保持时间，需要重新设计电路(例如可以通过插入buffer)的方式解决。

静态latch 和 register

如果需要用电路存储01这两种不同的状态，需要电路在高低电平时均能保持稳定，这需要构造一个双稳态电路。最简单的双稳态电路如下：

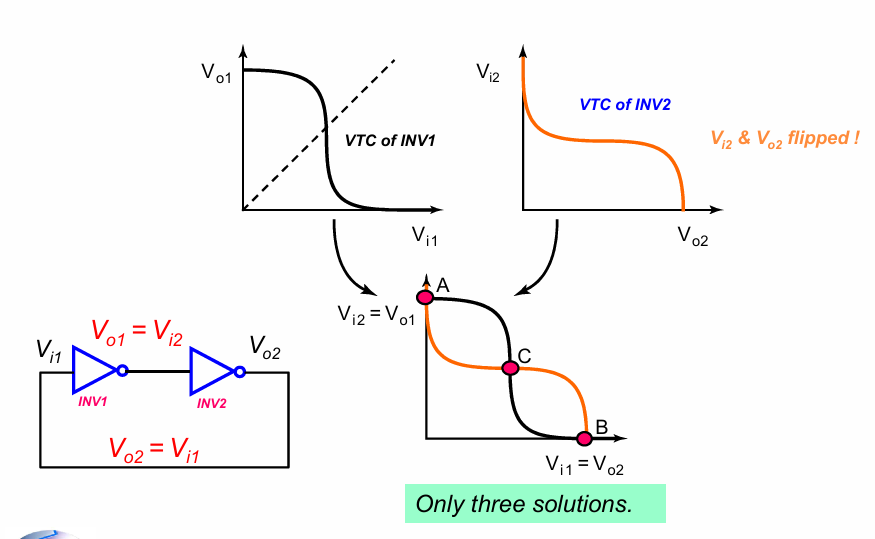
双稳态的蝶形曲线，可以保证任何向两端便宜的电压都会得到自我强化，最终达到一个稳定的端点：

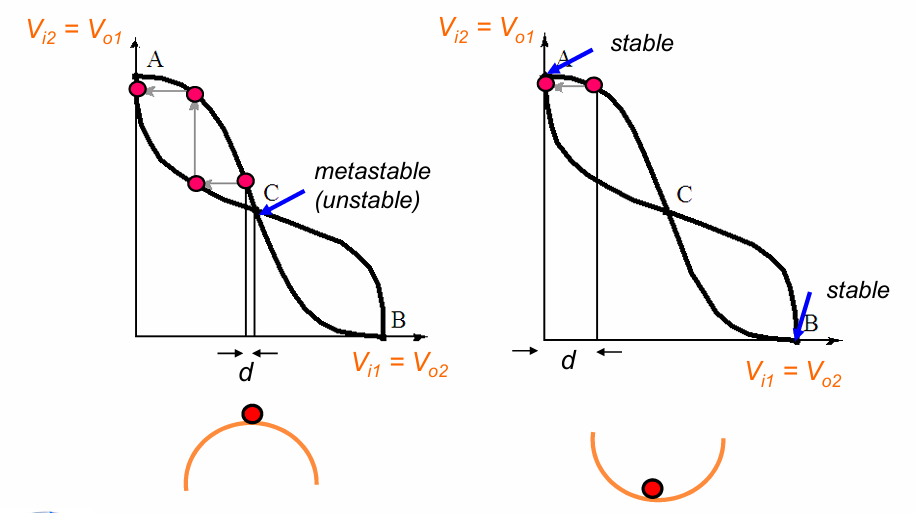
然而，注意到在电路的C端，同样是一个可能成立的点。如果电路停留在C点而没有任何外部绕的的话，则处于一种”亚稳态”。

数据的存储

使用晶体管存储电路一般有2种方式：

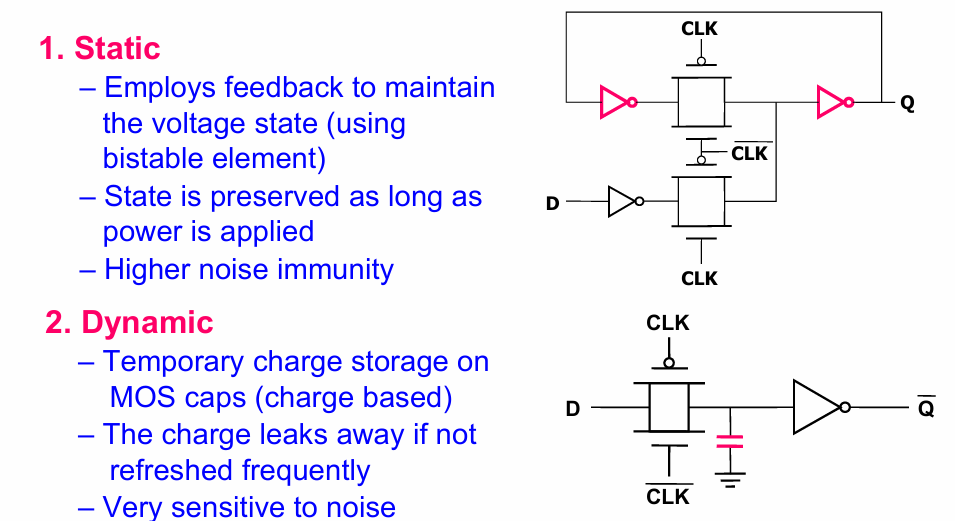
一种是通过双稳态电路静态存储，状态在通电状态下可以一直保存(类别SRAM)

一种是通过电容存储，需要定期刷新(参考DRAM)

数据的写入

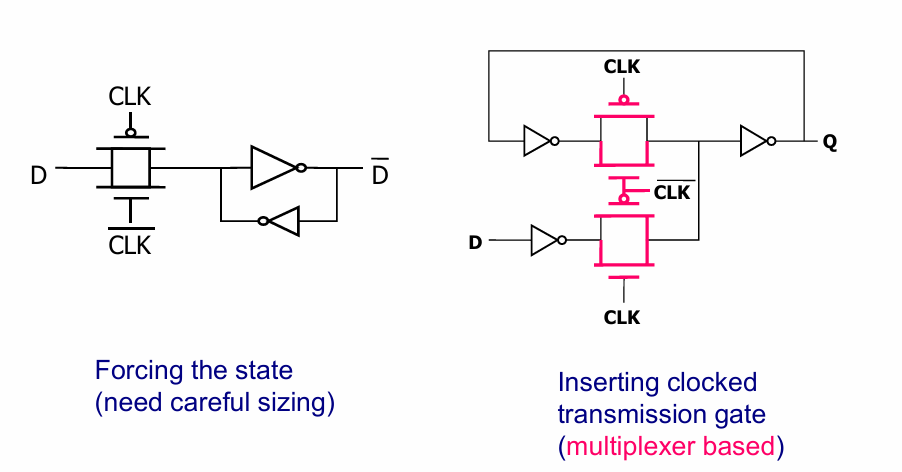
左边的写入方式是强行覆盖，需要晶体管有足够的驱动能力，需要sizing,右边的写入方式则相当于另外增加了写入通路。

latch的实现

基于mux的实现方式

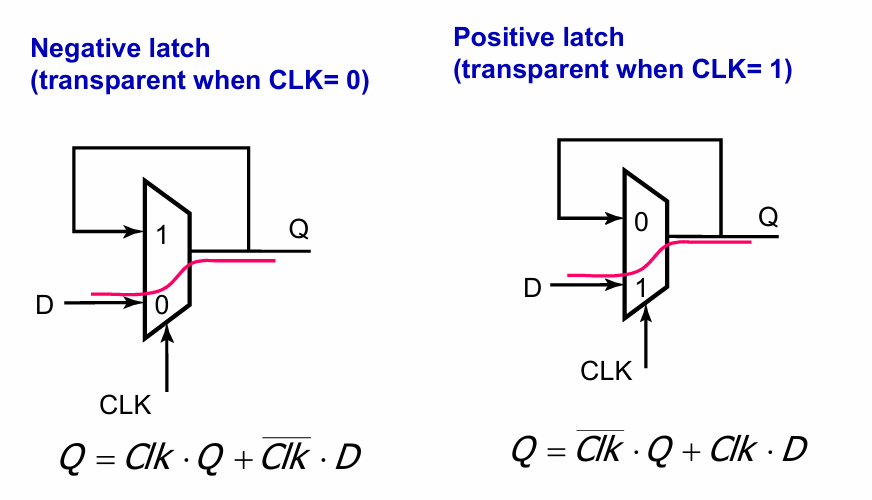
如图，通过反馈连接的Mux可以实现latch的功能

基于传输门的latch

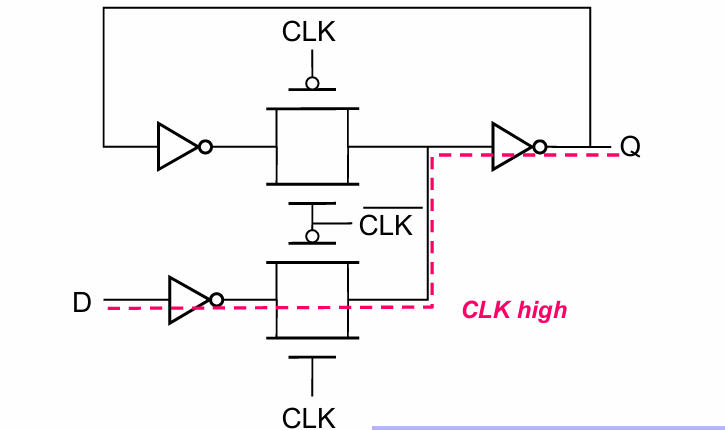
这种实现下clk信号要驱动4个负载晶体管

基于NMOS实现

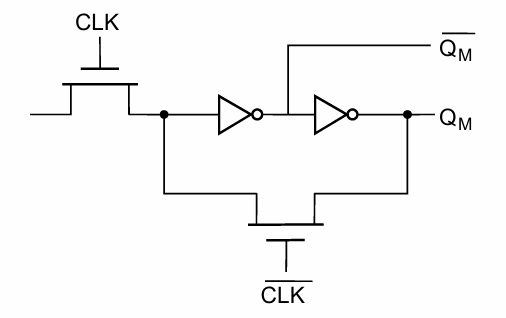
这种实现需要clk和clk非信号之间直接没有重叠

静态register的实现

register可以通过将2级latch进行串联实现(可以用船闸进行类比)

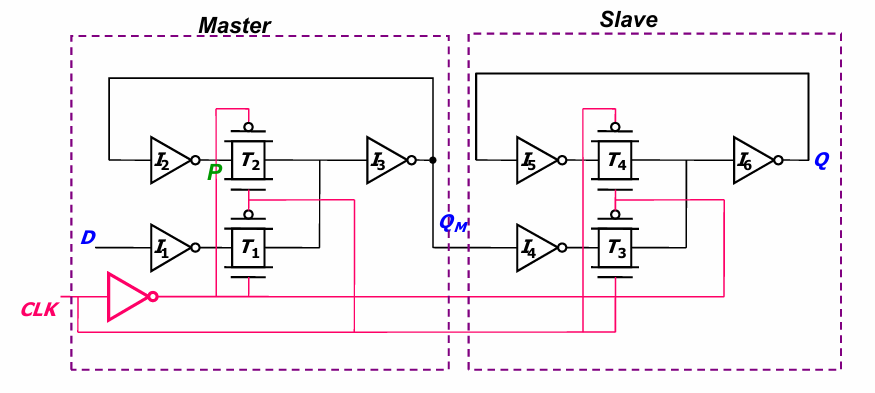
当clk为低时，数据被QM点采样，当clk为高时，QM保持不变并被Q采样。

此外，我们还可以对上述register做以下分析：

clk信号的负载是6个晶体管
建立时间：

分析上述电路的建立时间：
时钟上升沿到来之前(clk=0)，$T_1$打开，$T_2$关闭，信号D通过$I_1$,$T_1$,$I_3$,$I_2$（以及$I_4$）写入双稳态电路。如果不考虑分支造成影响，则建立时间为：

$$t_{setup} = 3t_{p_{inv}} + t_{p_{tx}}$$

即建立时间至少为3个反相器加一个传输管的传输延迟。

传输延迟

时钟上升沿到来后，$T_3$打开。Q端有输出，需要信号经过$T_3$,$I_6$,即：
$$t_{prop} = t_{p_{inv}} + t_{p_{tx}}$$

保持时间为0.这是因为一旦clk升高，$T_1$便关断，信号立即被阻断。

时钟交叠的问题

上述电路的问题在于，$\bar{clk}$信号是通过一个反相器产生的，而这导致原信号与非信号并不完全同步，会有时钟交叠的问题：

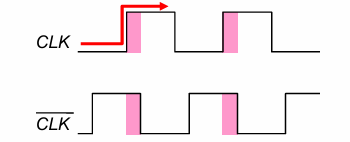
而当2个信号同时为高时，会存在从Q到D的直接通路，造成亚稳态。

可以通过2个不重叠的时钟解决上述问题：

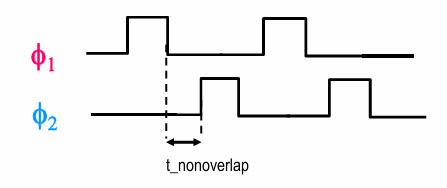
使用如下电路生成非交叠时钟信号：

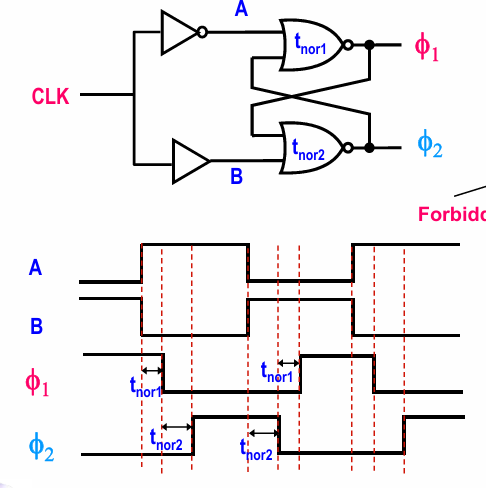
动态latch和register

静态latch和register的缺点在于电路一般比较负责，同时面积过大。同时，对于依靠时钟驱动的电路，信号值一般只需要暂时保存(例如几个clk cycle)，因此便有了动态存储的思想。

动态存储不使用双稳态电路中稳定的电平进行存储，而是使用电容中的电荷进行存储。

动态reg示例

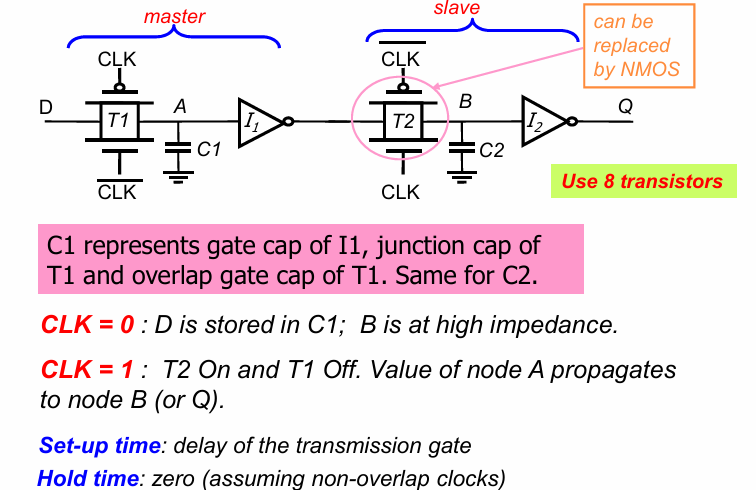
如图，使用一个大电容对电荷进行存储，同样能达到register的效果。

同时，可以在每一级Latch中增加一个反馈回路，使得电容的电荷更加稳定：

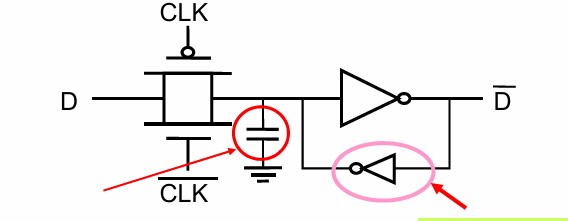
当然，即使做了改进，由于耦合，漏电和vdd跳变的影响，该电路的稳定性还是不如静态register。

其他类型的reg/latch

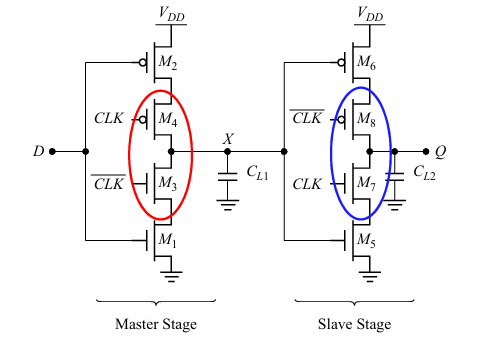
图中是一种C2MOS,当clk为低，$\bar{D}0$被写入X，当clk为高，X的非传到Q。

这种寄存器的好处是不存在时钟交叠问题，因为当clk和其非信号都为1或0时，D值无法传到X

单相register

上述寄存器的实现都同时用到了clk和其非信号，实际上还可以只用clk信号，从而避免时钟交叠问题。

如下所示：

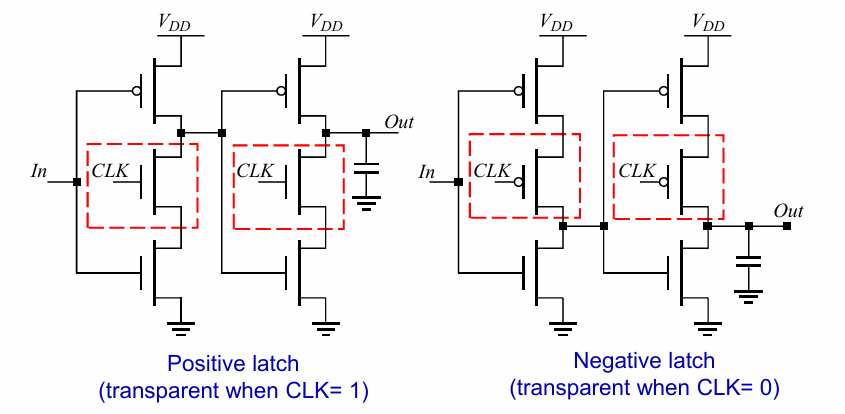
为了将上述latch变成register，首先将其拆分成2半：

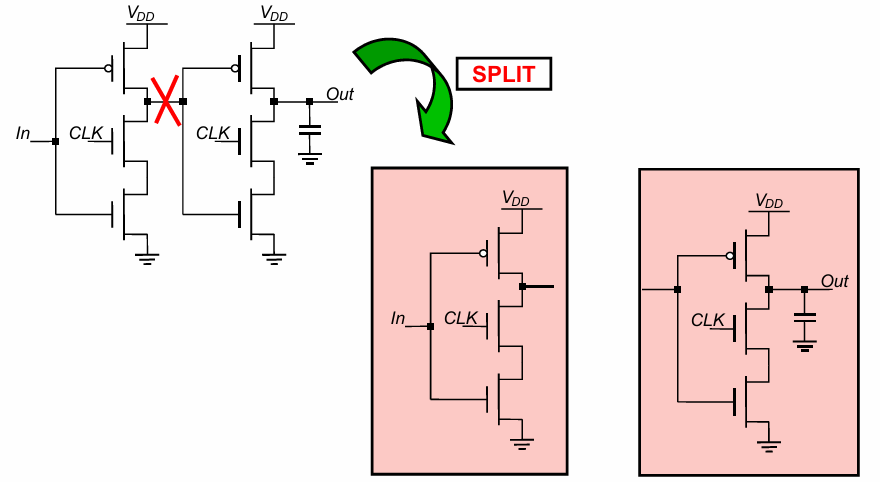
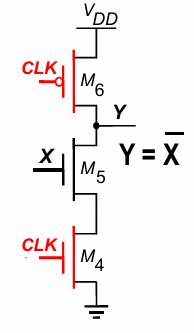
之后，我们加入一个动态逻辑中的inverter:

再将上述三部分合在一起，加上一个额外的反相器，即可构成一个register: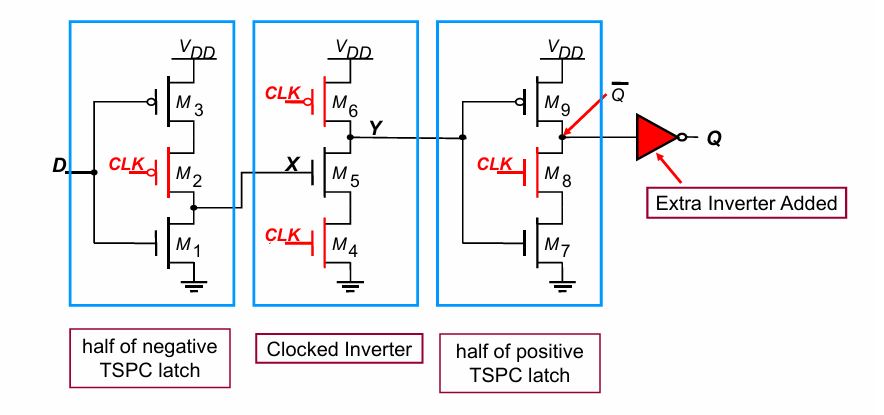

其工作原来如下：
clk=0时，D的非被传输到X，同时Y被预充为高。CLK=1后，Y点进行计算，得到X的非也就是D的值，同时Y的值经过半个Latch传到Q前面的反相器，再经过一级反相器达到Q。

其参数分析如下：

低功耗register设计

在现代处理器中，FlipFlops占据总功耗的约20%，因此低功耗的寄存器设计是有必要的。

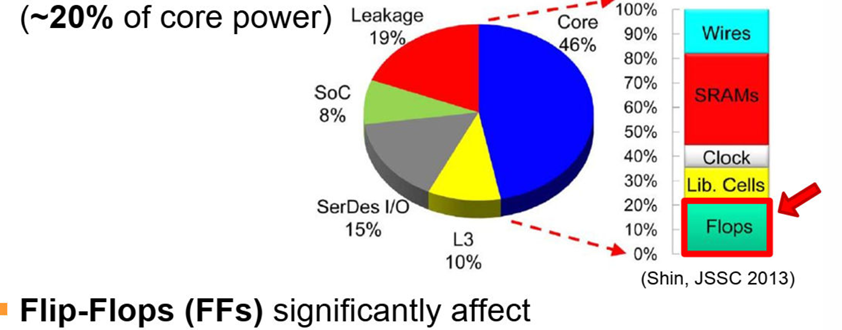
一个好的寄存器应当具有以下特点：

案例分析: S2CFF

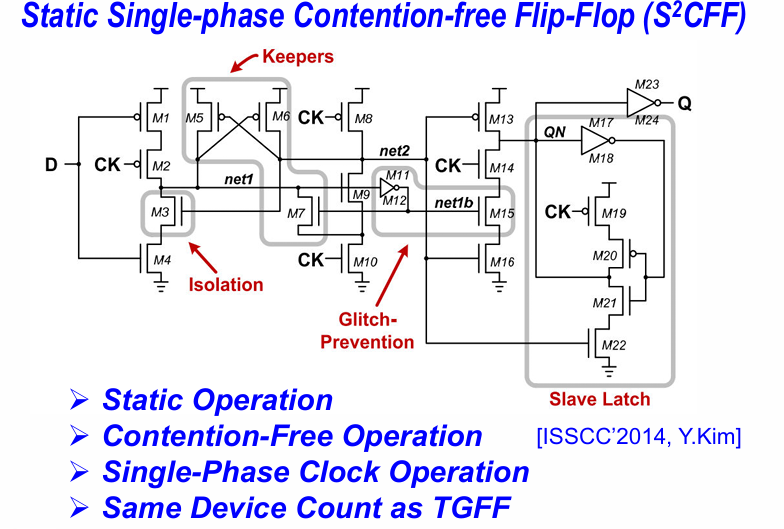
(待补充)

非双稳态电路

施密特触发器

施密特触发器的特性在于拥有非对称的电压阈值：

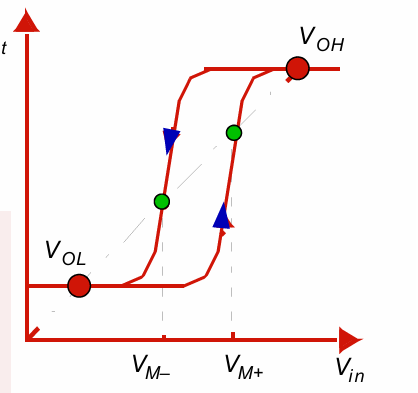
对于从低电压的传输，需要更高的电压阈值；对于低电压的传输，需要更低的电压阈值。

其电路符号如下：

施密特触发器一般被用作整流器，从而抑制电路的噪声：

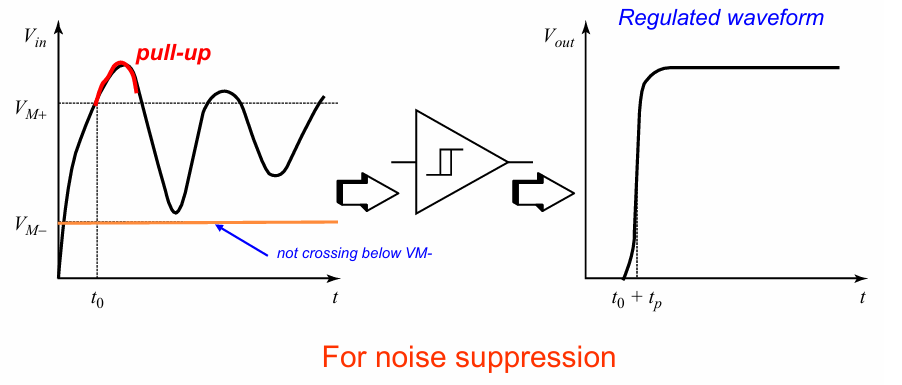
其CMOS实现如下：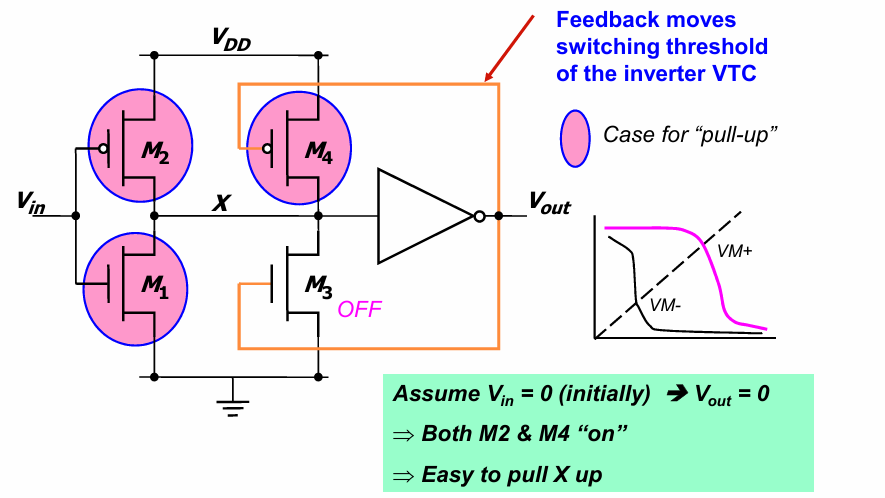

当VIN为0时，X为1，通过一个反相器的反馈，将M4打开，M3逐渐关闭，逐步将VOUT降到0.

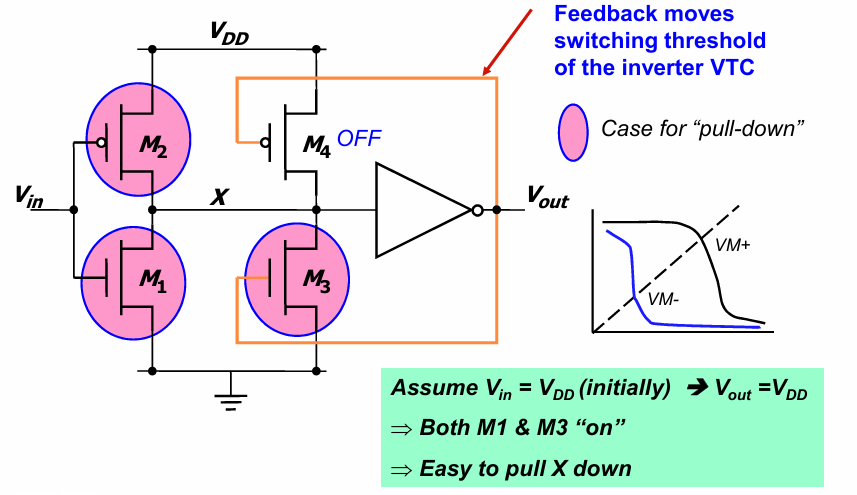
VIN=VDD时，通过M3逐步将X拉低，将VOUT升高到VDD

环形震荡器

(待补充)

Lecture6 低功耗设计

关于低功耗设计的内容占据3个课时

现代集成电路中的功耗问题

在数据中心服务中，功耗意味着成本，在高性能计算领域，功耗和散热制约着电路的性能，在移动端，功耗影响电池寿命。

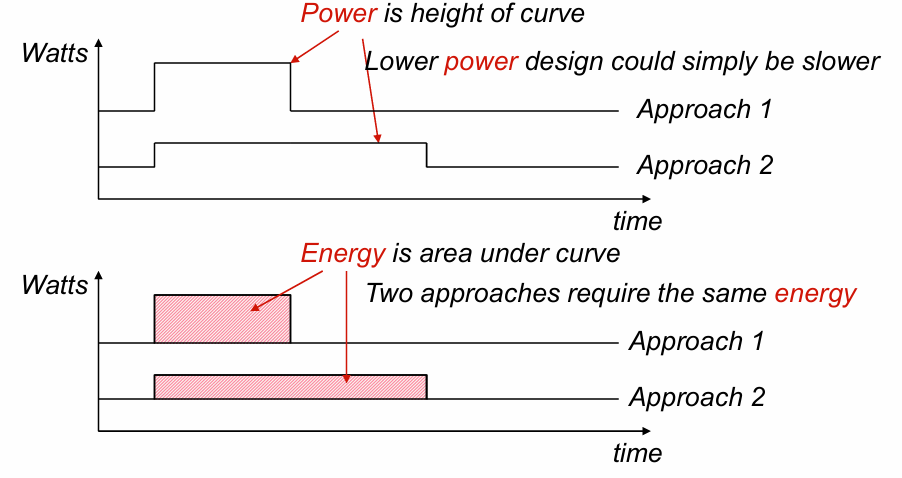
power vs energy

功耗和能耗是不同概念。

对于同一个计算来讲，消化的能量是功耗和时间的乘积(曲线的面积)，一个低功耗电路意味着电路的瞬时功率更小（曲线的高度），但是有可能因为耗时更长使得总能耗变大。

功耗分布情况

集成电路中，功耗分为静态功耗，动态功耗和静态电流(DB端的反偏PN结电流)

动态功耗

动态功耗正比于翻转频率：

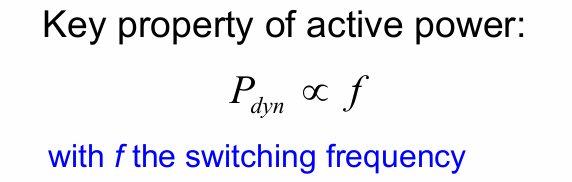
动态功耗的的来源有3个：

电容的充放电
电流翻转过程中的短路电流
临时产生的毛刺(gliches)

电路功能对动态功耗的影响

由于CMOS电路的动态功耗只与输出从0向1变化有关(参见前面对反相器的分析)，所以动态功耗的表达式如下：

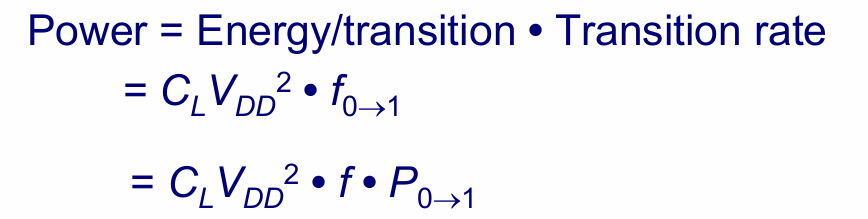
假设输入的概率均匀分布(0和1各占一半)，则相同时钟频率下，不同逻辑功能从0翻转到1的概率不同。

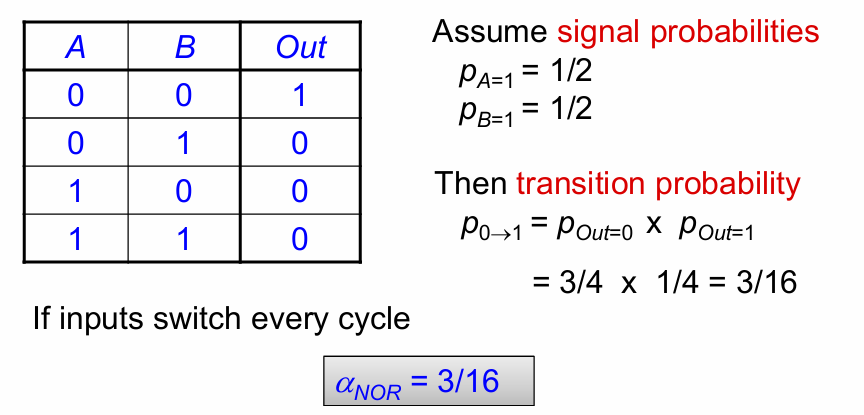
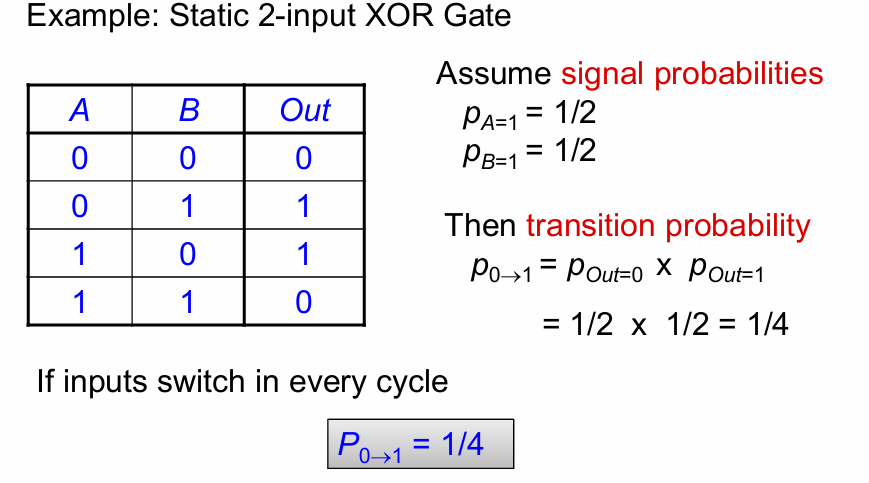
这个概览在多级或多输入的情况下更加明显：

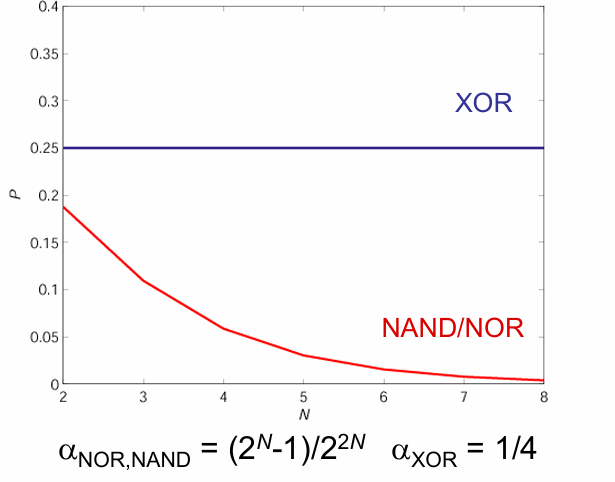
而对于动态逻辑，差分逻辑来讲，其动态功耗都大于CMOS逻辑。

CMOS中的毛刺

考虑如下电路：

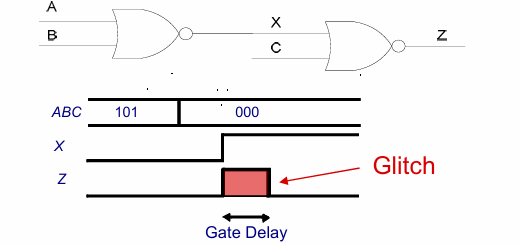
ABC同时由101变为000，在AB由10变为00时，输出信号X由0变为1，这个时间晚于C，导致中间有一个阶段，X=0,C=0,Z被短暂的拉高。当X完成计算后，Z又被重新拉低。

这种问题也被称作动态冒险(dynamic hazard)：是指输入的一次变化造成了输出的多次变化。

分析这种毛刺产生的原因，是因为最后一级逻辑门的输入没有同时到达。

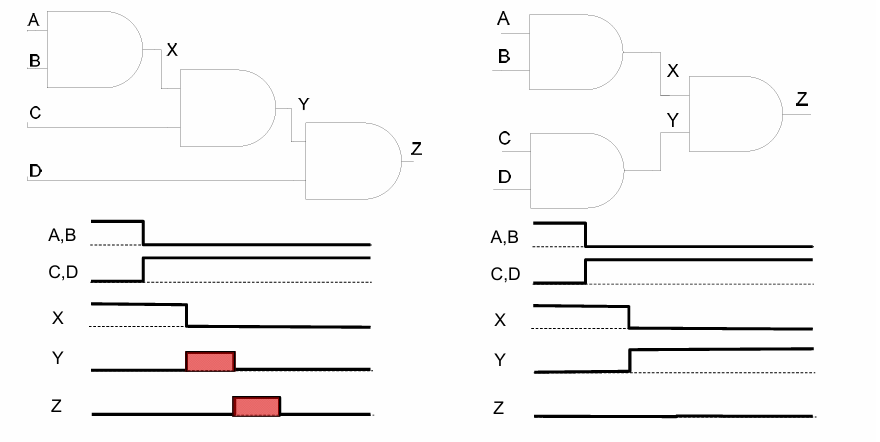
如果重新调整电路的结构，使各条路径上的延迟尽量平衡，则可以消除掉相应的毛刺。

短路电流

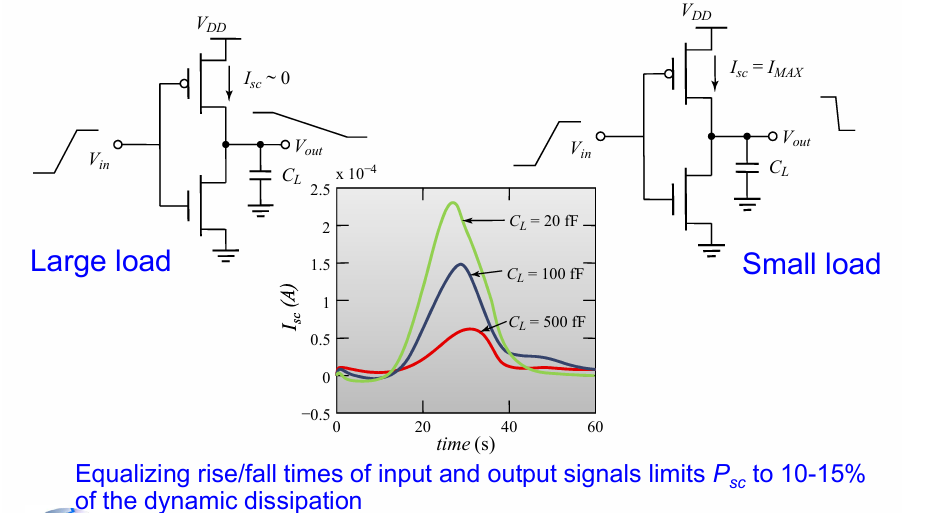
短路电流产生的原因是在输出翻转的过程中，有一个阶段上拉网络和下拉网络同时导通。

通过调整上升延迟和下降延迟的时间尽量相等，可以把短路电流功耗占据动态功耗的比值降低到10%~15%

静态功耗中的漏电流

亚阈值漏电 sub-threshold leakage

一般而言栅电压低于阈值电压时，我们认为晶体管被关闭。但晶体管并非理想器件，实际上在关闭时仍存在漏电流。且器件的阈值电压越低，这个漏电流越大，且呈指数增长。(这也是为什么finfet效果更好，因为关断的效果更明显)。

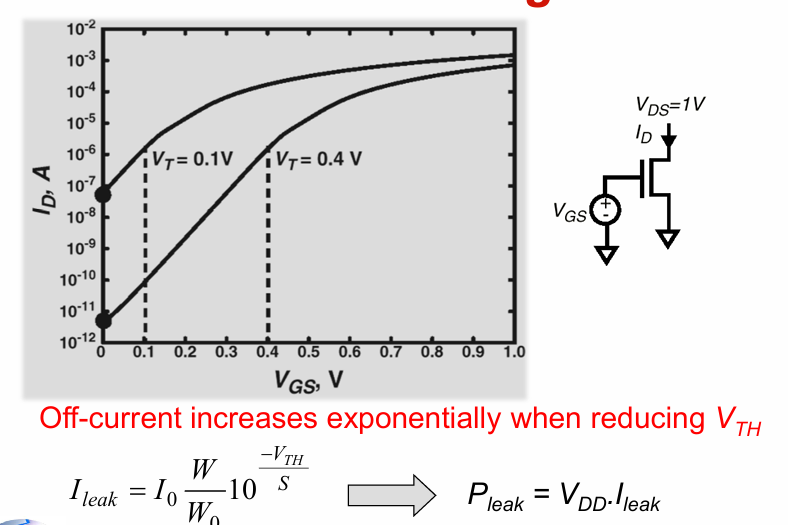
堆叠效应 stack effect

有趣的是，当多个管子堆叠时，可以有效降低亚阈值漏电：

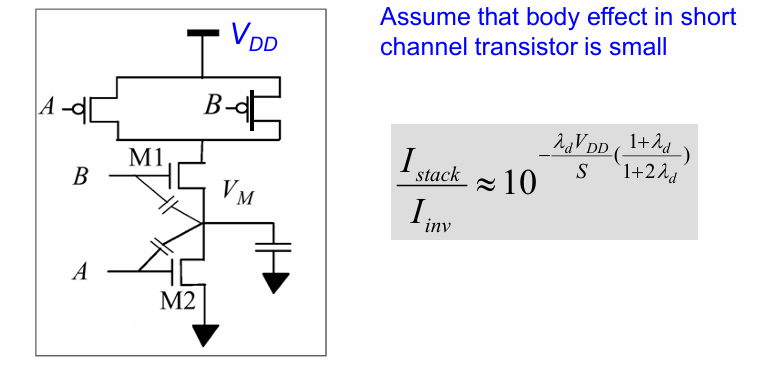
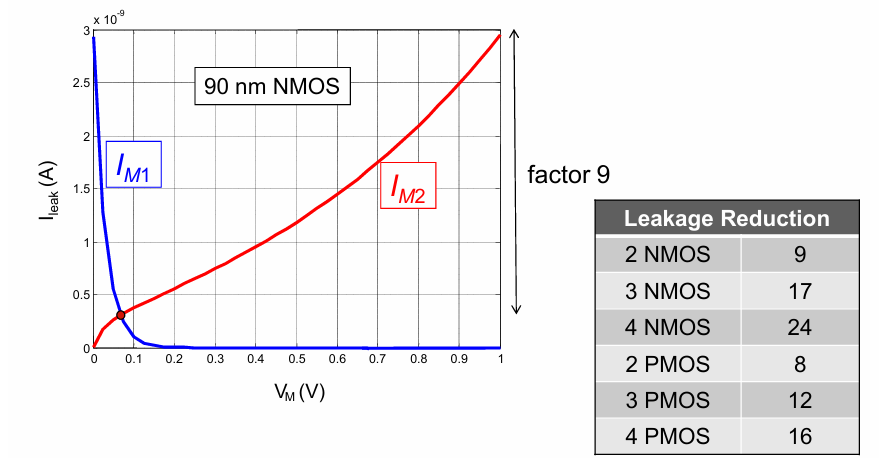
然而，堆叠效应同时也会造成电荷共享问题。

低功耗优化策略

针对不同的功耗和电路工况，可以总结出如下所示的低功耗优化策略矩阵：

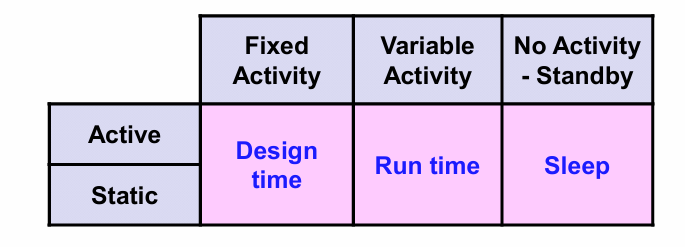
不同的优化测量分布对于矩阵中的如下位置：

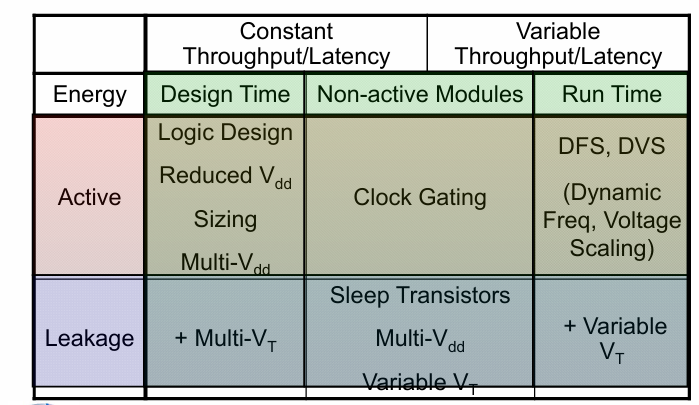
多电压域 multiple supply voltages

分为2种，一种时block内的多电压，一种是不同function块的多电压。

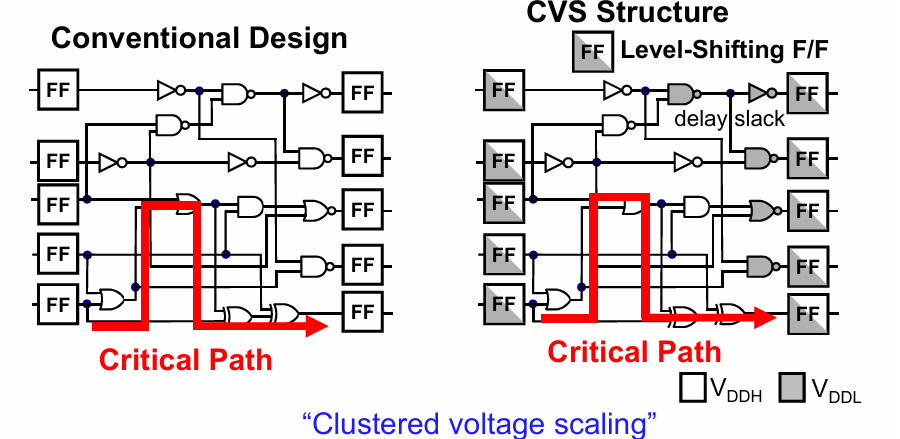
例如可以针对同一个组合逻辑中的关键路径提高电源电压，以达到更快的计算速度。其他模块则采用较低的电压。

上升电路中的电压转换寄存器(level convertiong FF)的实现方式如下：

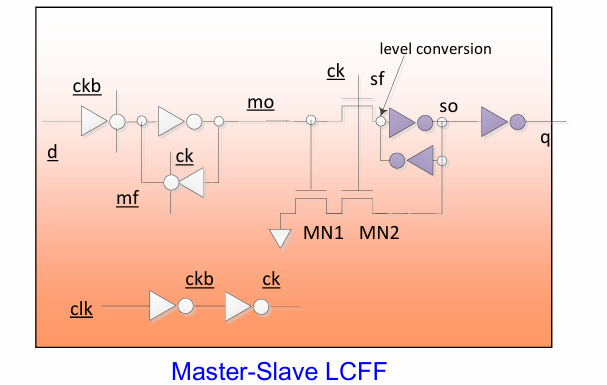
可以实现d=vddl,q=vddh的变化

通过模块内的多电压域技术，实际上是提高了非关键逻辑的延迟。由此带来的问题是，改变了不同路径的延迟分布，有可能带来电路稳定性的问题（从统计学的角度）：

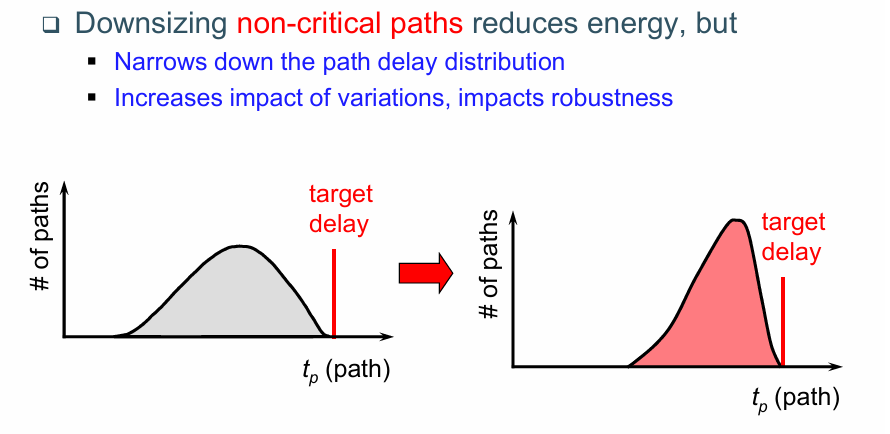
具体的多电压域有以下2种实现方式：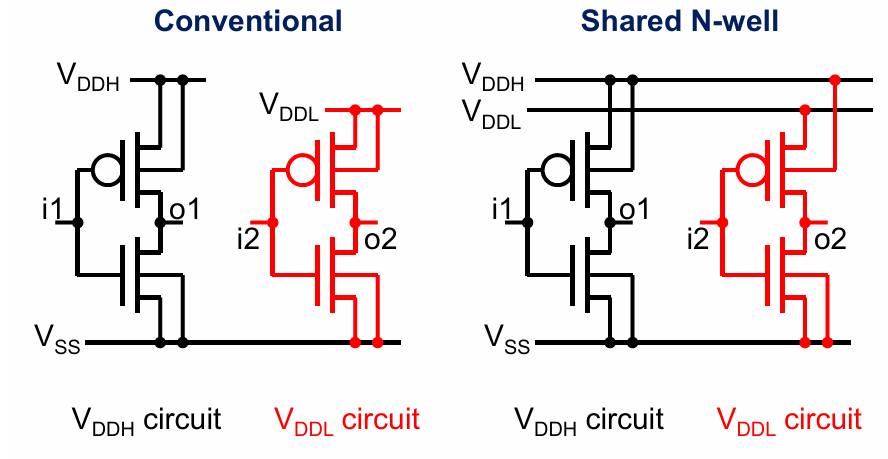

降低电源电压 supply voltage reduction

数字IC中一个典型的数据通路如下：

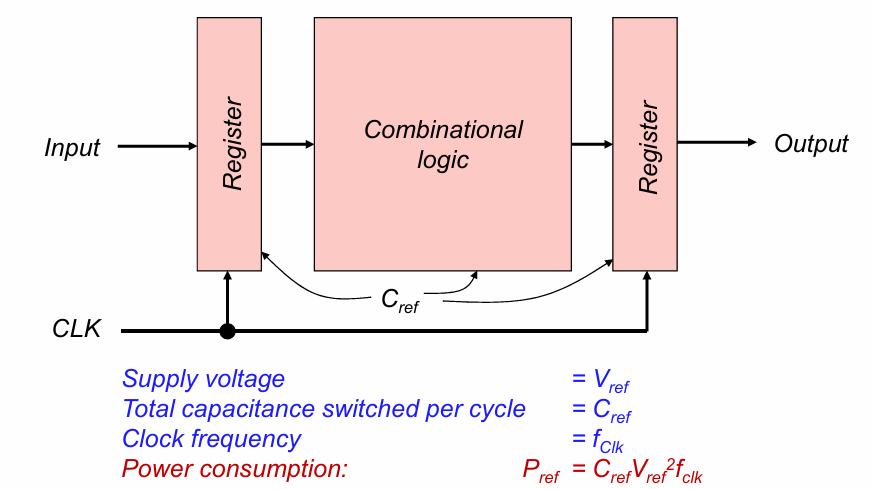
其功耗与电源电压的平方，以及电容，电路的频率成正比，因此理论上降低这三个值中的任何一个都可以有效降低功耗。

并行降低功耗

通过并行技术可以有效降低电路的功耗，其原理如下：

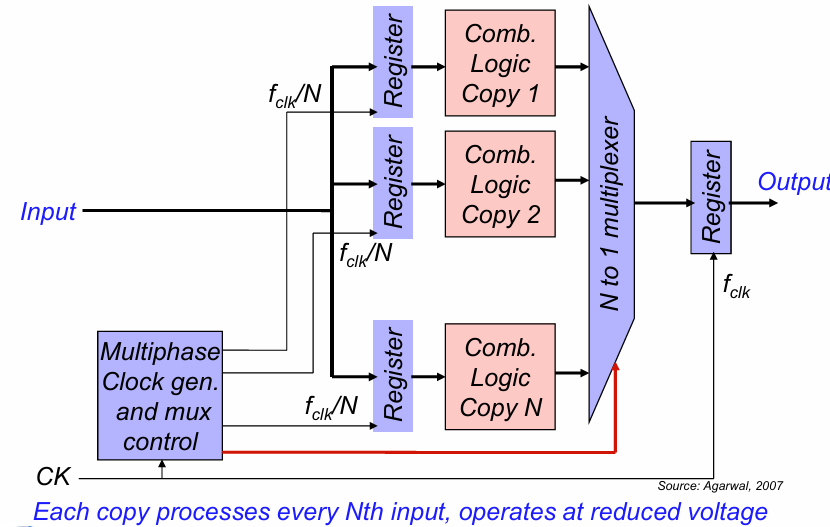
通过将组合逻辑的硬件复制多份，将其计算能力提高N倍。
注意，组合电路执行的并不是相同的逻辑运算，而是分时运算。

例如，如果将前面采样寄存器的时钟周期保持不变，而在每个周期内送入n组不同的输入，它们分别被送入不同的n组组合电路中进行运算。经过原来的一个时钟周期后，所有计算完成。将输出频率提升n倍，通过mux将其结果输出，就可以在原来的一个时钟周期内得到n个不同的计算结果，相当于将电路性能提升了N倍。

而低功耗技术则是保持末端采样的频率不变，而将前方的采样频率降低为原来的1/N。由于采样频率的降低，组合逻辑可以用更长的时间完成计算，因此可以降低电压。

更细节的分析如下：

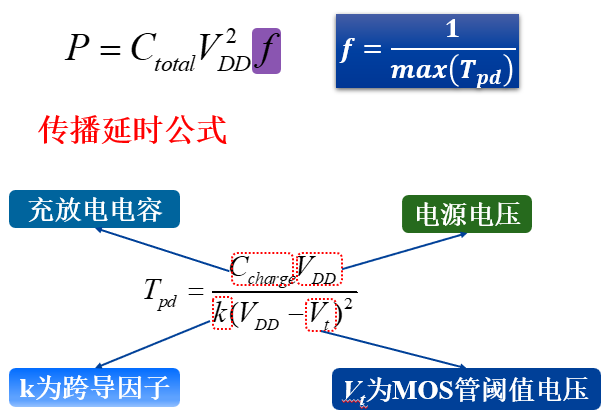
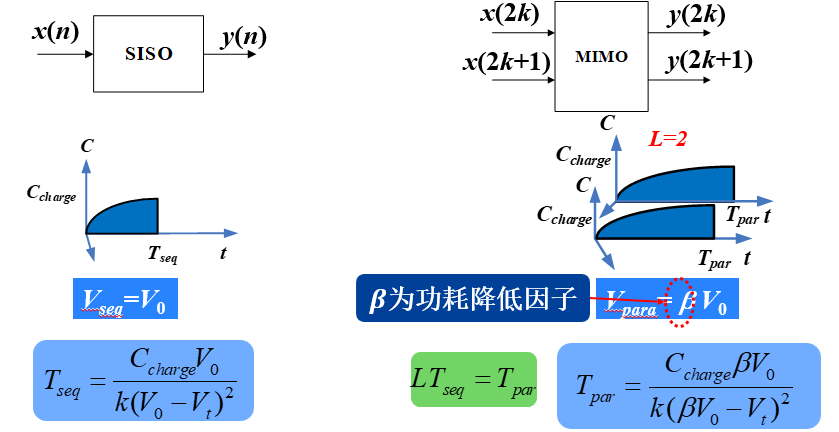
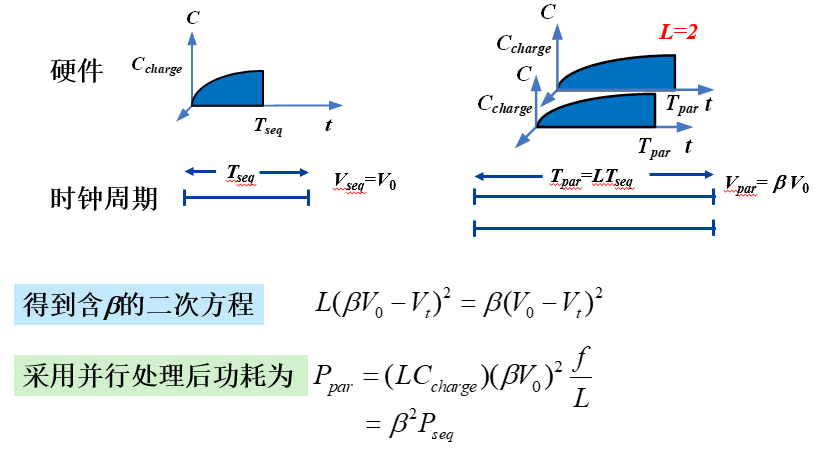
即通过并行后将电源电压降低为原来的$\beta$倍，功耗降低为原来的$\beta^2$倍。

流水线降低功耗

流水线降低功耗的原理是，通过流水线提高电路的工作频率，然后降低工作电压，最终达到降低功耗的目的：

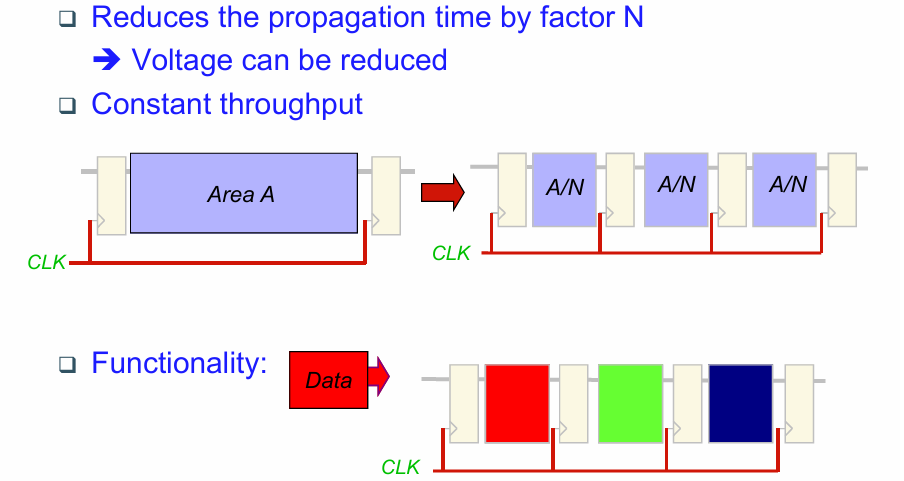
不同方法的总结如下表：

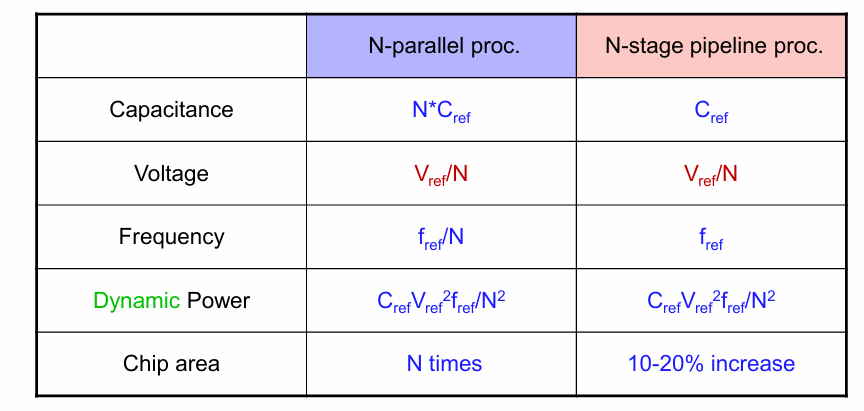
DVFS Dynamic voltage and frequency scaling

动机：在实际应用中，电路的活动频率和时间的相关性很大。例如在PC的日常使用中，CPU大部分时间是在待机，只有少部分时间执行高密度计算任务：

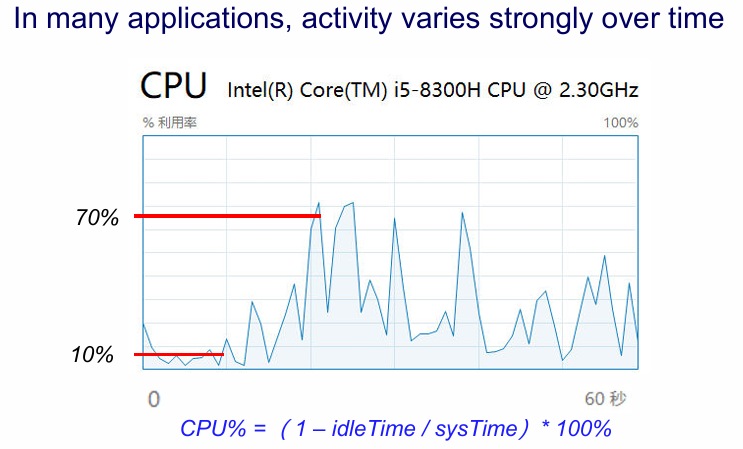
如果单纯降低工作频率，无法满足高性能计算的实时性要求：

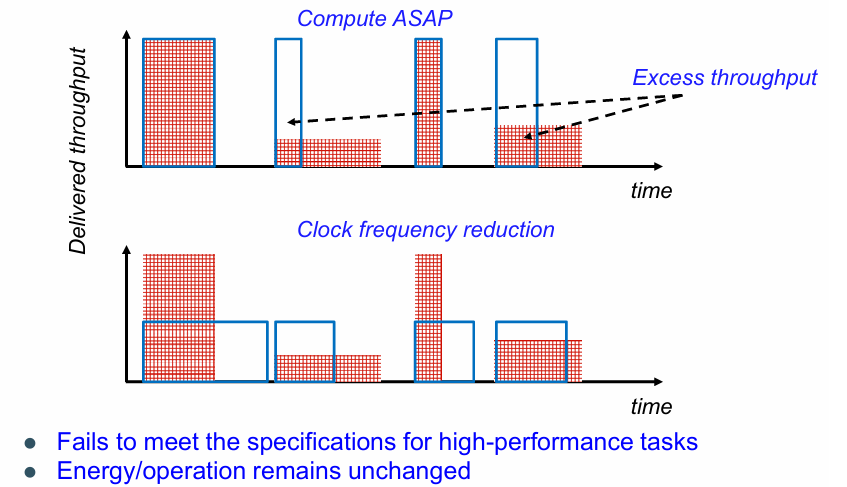
通过DVFS技术，则可以有效提高电路的瞬时性能，而保持总能量消耗不变：

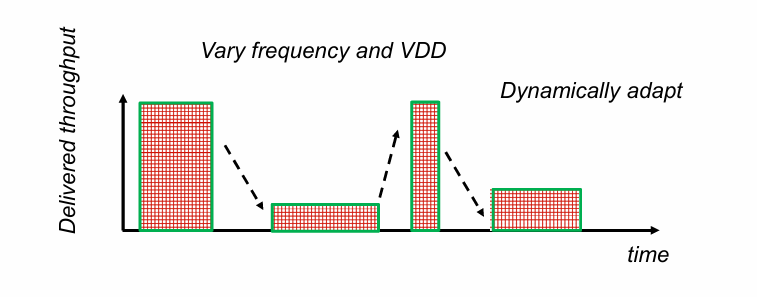
(这有点像人，同一件工作如果紧急，就提高效率争取快速做完。如果并不很着急，就暂时摆烂慢慢完成)

电源电压和工作频率的关系如下：

在先进工艺下，频率和电压基本成线性关系。

DVFS框架

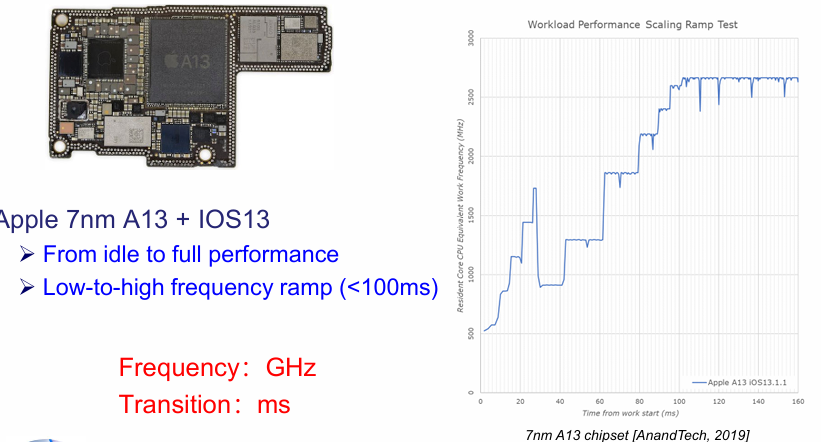
一个典型的DFVS框架如下：

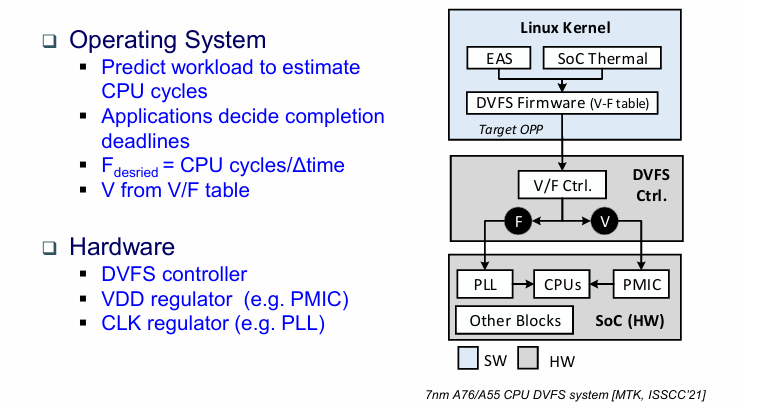
应用来决定任务的DDL,操作系统根据性能评估CPU的工作负载，选择合适的电源电压和频率节点。

通过软件控制硬件完成相应的DVFS操作。

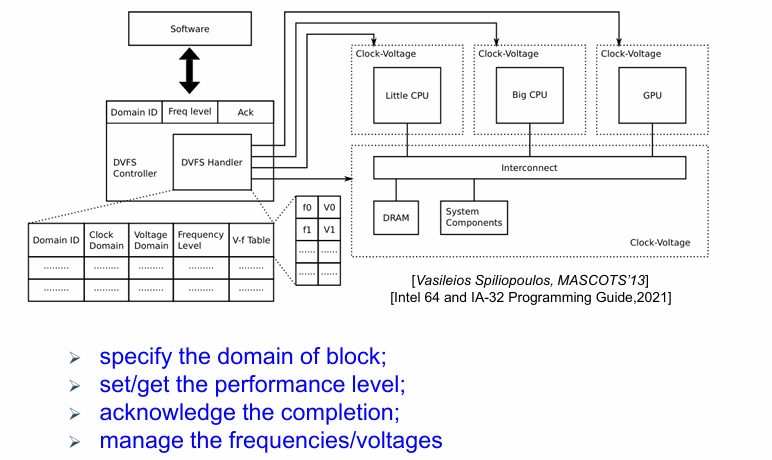
例如，对苹果A13处理器，从待机到全功率运行需要大约100ms的时间：

DVFS的开销

DVFS会对系统造成额外开销，主要有以下几个方面：

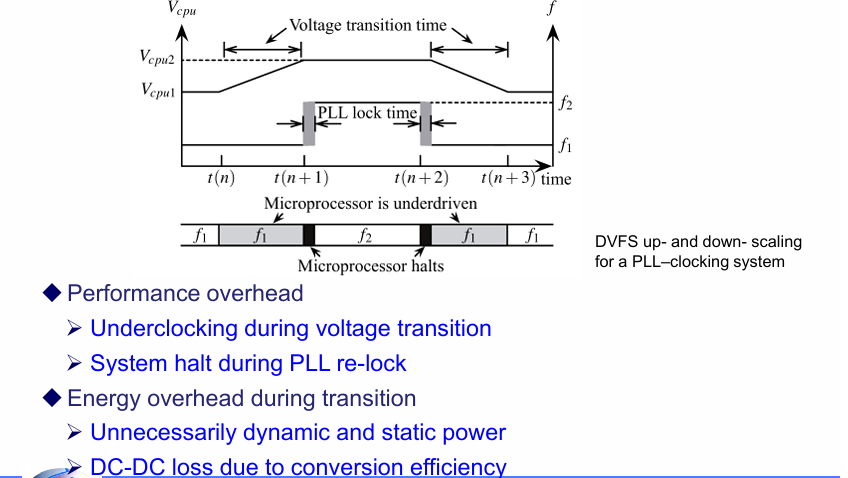
clock gating technique 门控时钟技术

通过为时钟信号加上一个disable（或者enable），实现时钟的控制，后面的电路在没有时钟信号时都不再翻转，从而省电。

相应的verilog代码如下：

通过clock gating技术可以显著减少能耗(70%)

power gating 电源门控

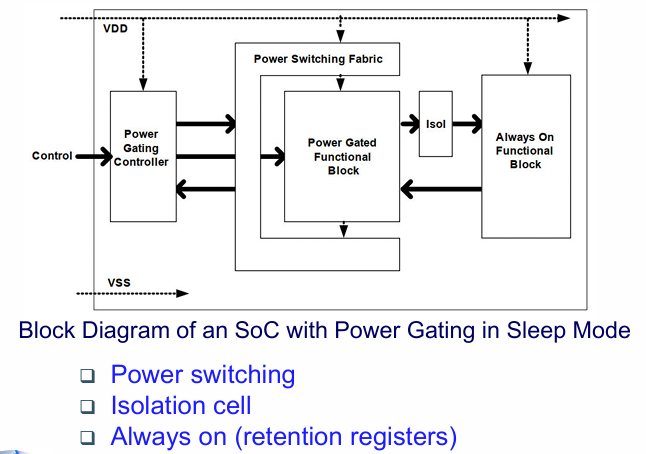
电源门控控制器（Power Gating Controller）：控制芯片中关断模块的电源何时关闭并给特殊的cell如retention register输出必要的使能信号；
电源切换结构（Power Switching Fabric）：也称电源开关（Power Switch），实现电源关闭的逻辑单元，一般由后端实现阶段加入并按照一定规则摆放；
始终开启模块（Always-on Module）：电源一直保持打开的模块；
隔离单元（Isolation Cells）：简称ISO，一般在关断模块到电源始终开启模块方向的信号需要加入此类cell；
保留DFFs（Retention DFFs）：特殊的寄存器能够在主电源关断的情况下保持数据不丢失，只有当关断电源时仍然需要保留部分数据的时候才需要此类cell。

门控电源域

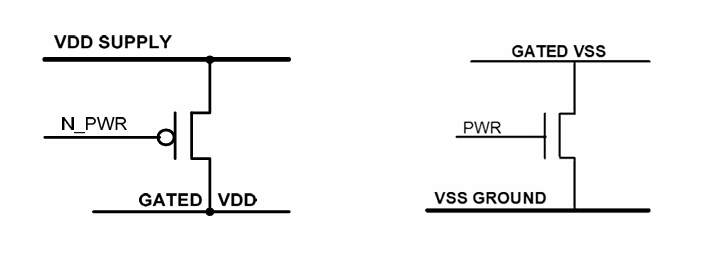
通过门控决定电源是否接入或接地。

一般使用基于PMOS的”header”,有时也使用基于NMOS的”footer”。在实际应用中，电源门控的方式主要有两种：关闭VDD或者关闭VSS，但在实际应用方面以关闭VDD为主。

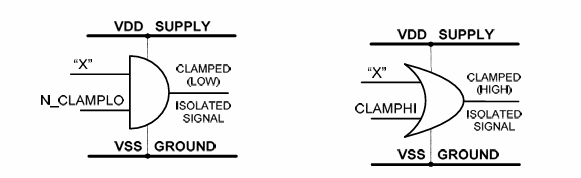
隔离单元 ISO

隔离单元在电源关断（Power Gating）技术中的主要作用是在模块的电源被切断时，隔离该模块与其他模块之间的信号传递，防止因模块电源关闭而对其他模块产生影响。也就是说，当一个模块的电源被关闭时，隔离单元可以阻断该模块的输出信号，防止这些信号对其他模块产生干扰。

方法是通过产生纯净的0或1信号。

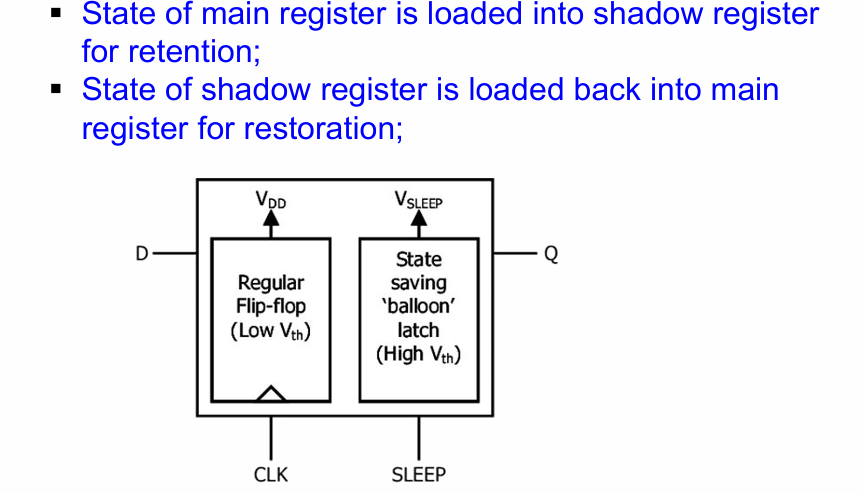
数据保留 data retention

添加Power gating 的示例

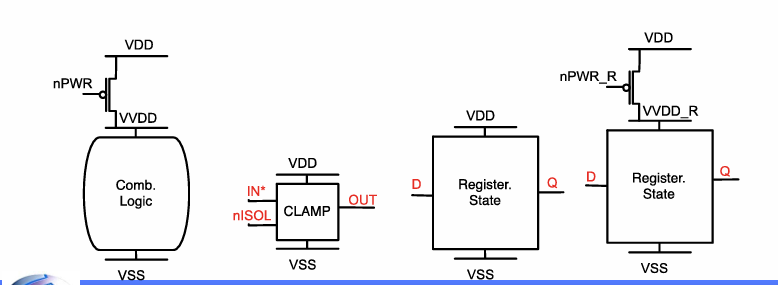
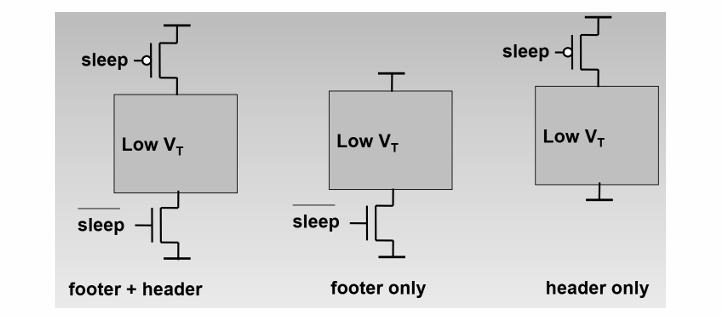
使用高阈值晶体管实现，N管比P管节约更多面积。

门控电源的问题

门控电源会带来2个问题：

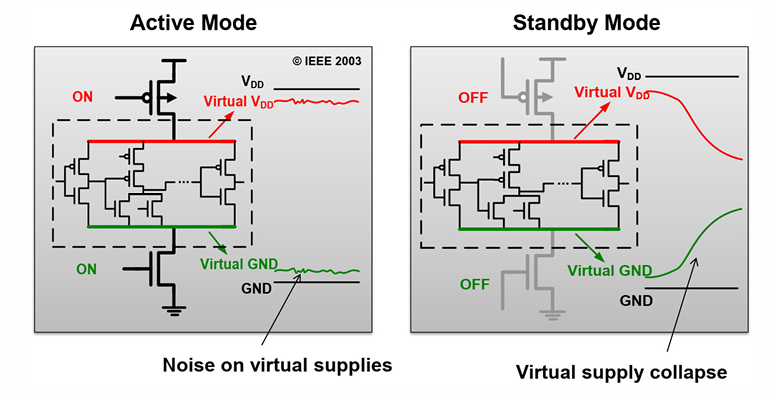
由于门控电源的加入，工作时虚拟vdd 和虚拟vss 2根线上可能存在噪声。

当模块关闭后，虚拟功能线上的电压很快发生变化，电路中保持的状态迅速丢失。

添加解耦电容 decoupling capacitor

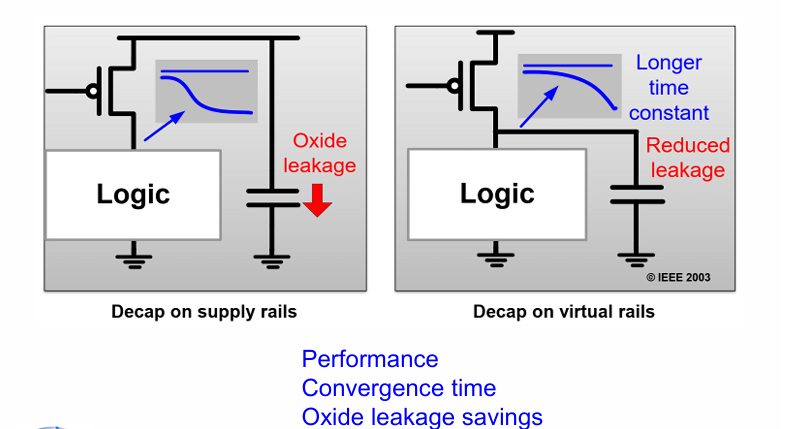
解耦电容可以有效保证电路工作时的性能，同时让其中的信号更长时间保持稳定。也能够有效降低氧化层漏电。

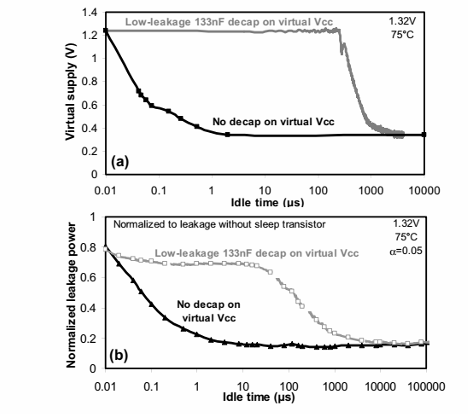
苏醒时间问题

传统的门控电源在休眠后，需要很长时间苏醒才能正常工作(大约1k~1M时钟周期不等)，这使得对于一些只需要短期休眠的任务无法应用。

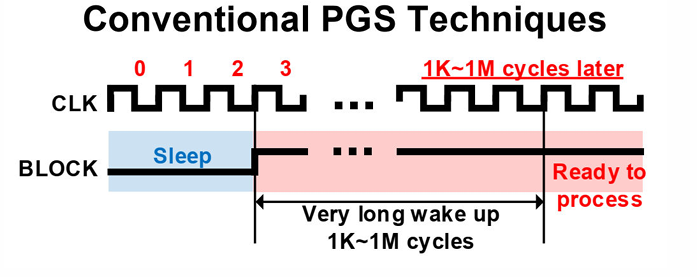
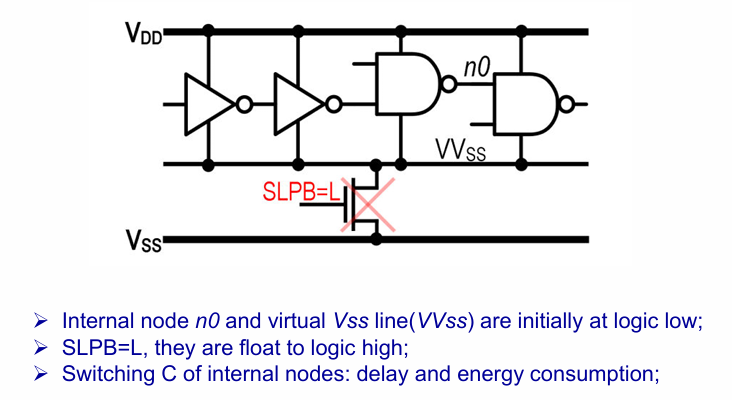
苏醒时间慢的原因是需要对电路的中间节点通过footer进行放电。

一种改进方案：

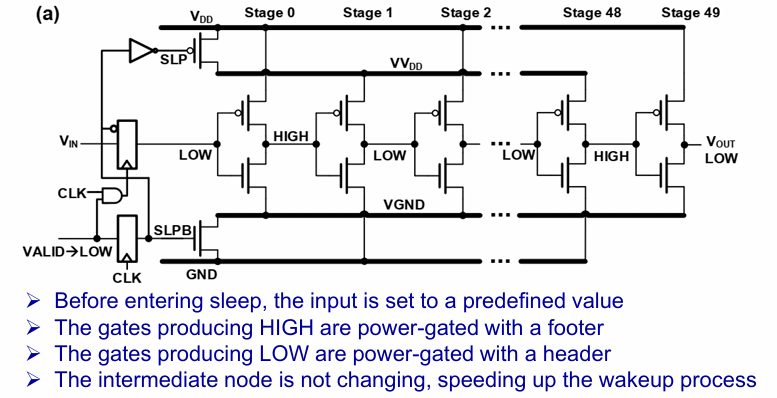
体偏电压调节

通过第二节器件的知识我们已经知道，晶体管的阈值电压与体效应有关，通过调节体偏电压的大小，可以控制阈值电压。而阈值电压决定漏电流的大小。

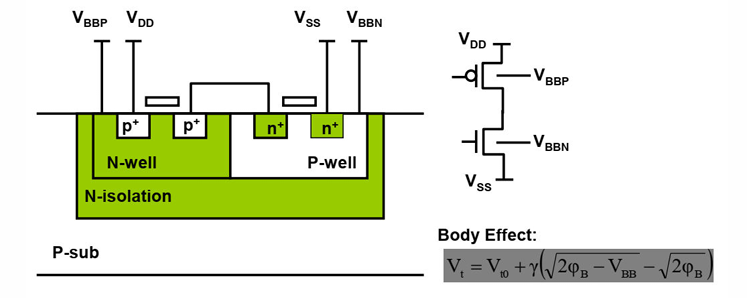
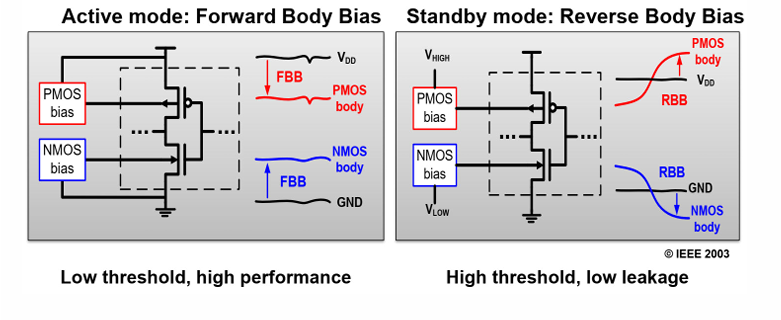
动态体偏电压的调节有2个思路：

电路工作时，设置为正偏，降低VTH,提高性能
电路休眠时，设置为反偏，提升VTH，降低功耗。

Supply Voltage Ramping (SVR)

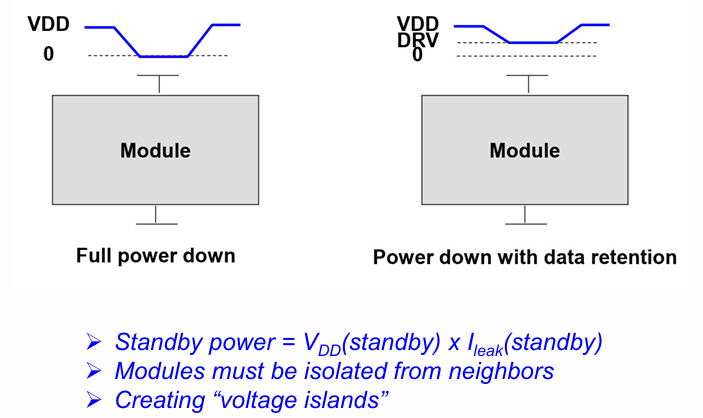
在休眠时，干脆关闭电源电压或降低电源电压，以进一步节约功耗。

可以有效减小漏电流

power gating总结

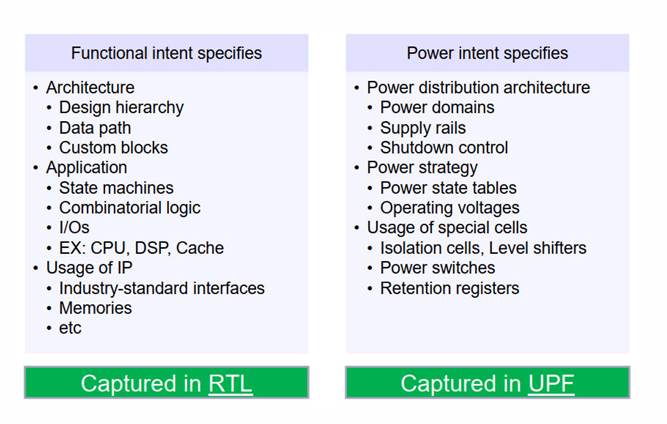
超低电压计算

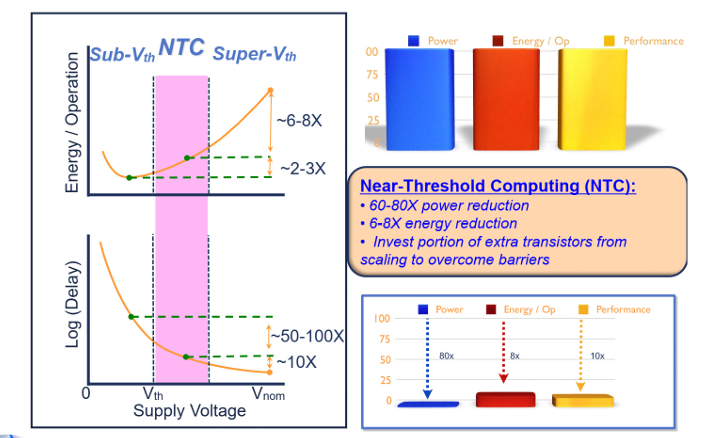
要获得最高的计算性能，需要将工作电压提高，以加快电路的计算速度。
然而如果想要是电路每次操作的耗电达到最低，则工作电压降低到阈值附件。

在一些边缘侧的供电受限，且不需要高性能的设备中，这类设计是很有用的。

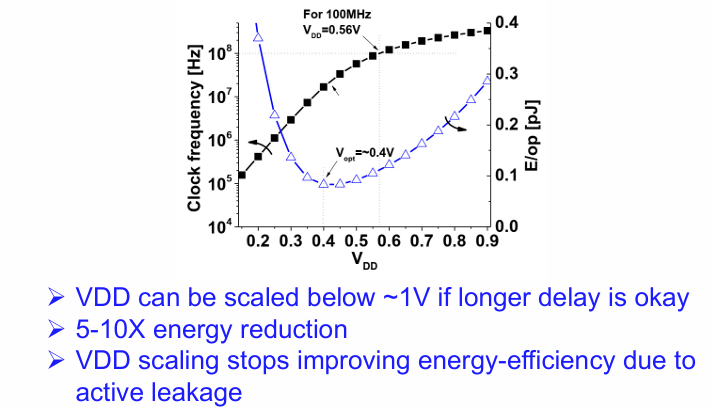
工作电压VDD不能无限降低，因为再低下去电路的漏电会很大。

logic sizing

在超低电压下，漏电电流变得和驱动电流大小接近。需要考虑电路的sizing问题。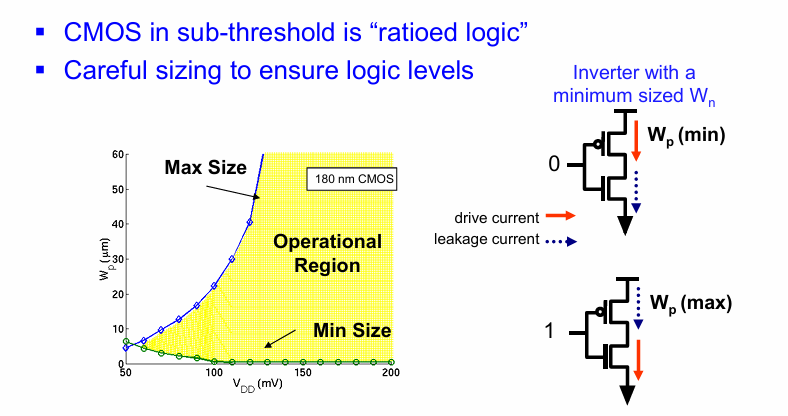

同时要考虑工艺角问题：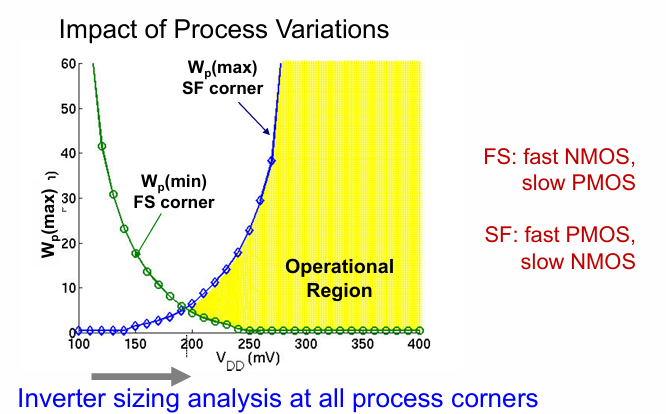

Dynamic Leakage-Suppression Logic 动态漏电流抑制

(待补充)

Variation Adaptive Circuits 自适应电路

Timing Resilient Circuits

（待补充）

Lecture7 Arithmetic Circuits 算数电路

加法器

加法器作为算数逻辑运算的基石，很多时候也是电路的性能瓶颈。
对加法器的优化主要在于2方面：

全加器

全加器接受3个输入信号(A,B,$C_i$)和2给输出信号(S,$C_o$)。又被称为3-2压缩器。

其中输出和输入的逻辑如下：

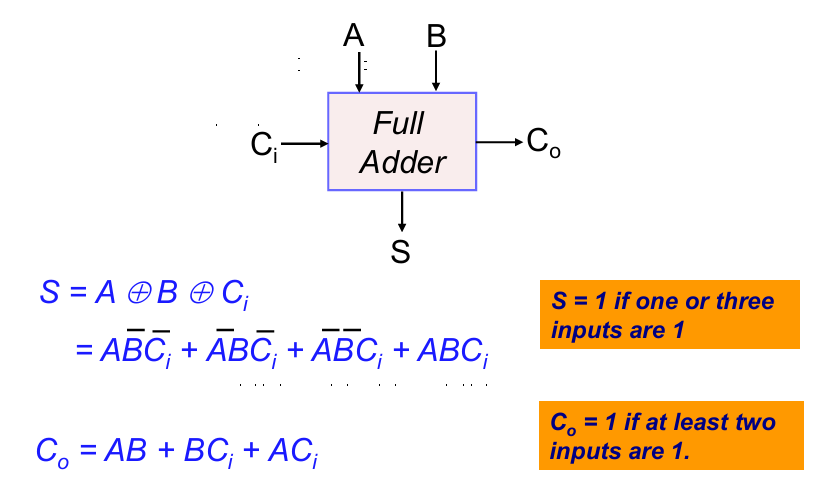
此外我们还可定义如下的中间变量，用于后续推理。

$$G = AB $$
$$P = A\oplus B$$
$$D = \bar{A}\bar{B}$$

其中G代表generation,表示进位的产生。P代表propagation，表示如果上级产生一个进位，则可以被传播到下一级。D代表delete,表示任何进位都会在这一级消失。

行波进位加法器 The Ripple-Carry Adder

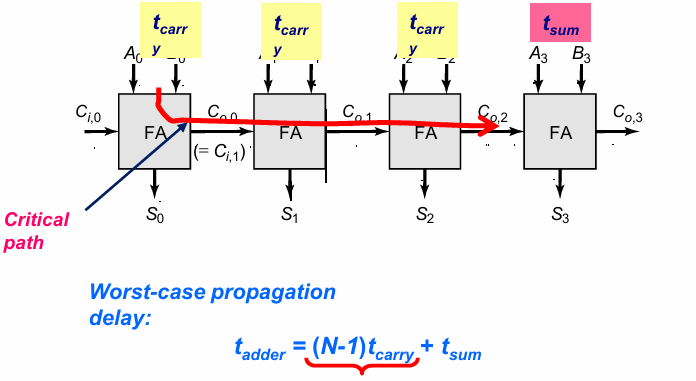
一个最简单的加法器实现就是将多个全加器串联，得到行波进位加法器。其中进位由低到高逐级产生。

电路的关键路径是n-1级的进位加上最后一级的求和。

这样的加法器，其关键路径延迟是很长的，与加法器的位宽成线性关系。

全加器的电路架构

我们重构全加器的逻辑表达式：

上述逻辑可以用以下的28管CMOS电路实现：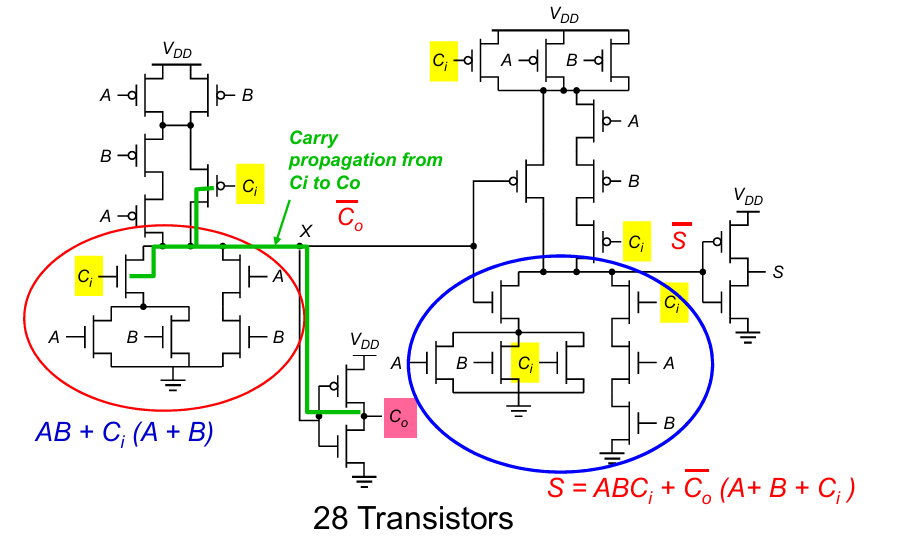

上述实现的优缺点如下：

改进措施

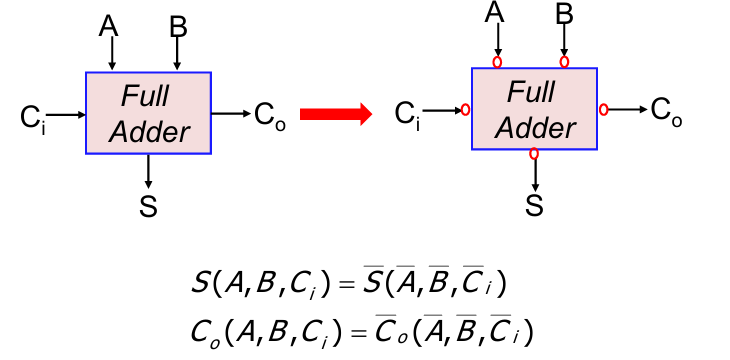
同一计算逻辑，如果将输入反向，输出逻辑也反向，则得到的结果不变。

通过将奇偶方向加上或去掉反相器，最终每4位可以去掉2个反相器，同时在关键路径上减少了4个反相器：

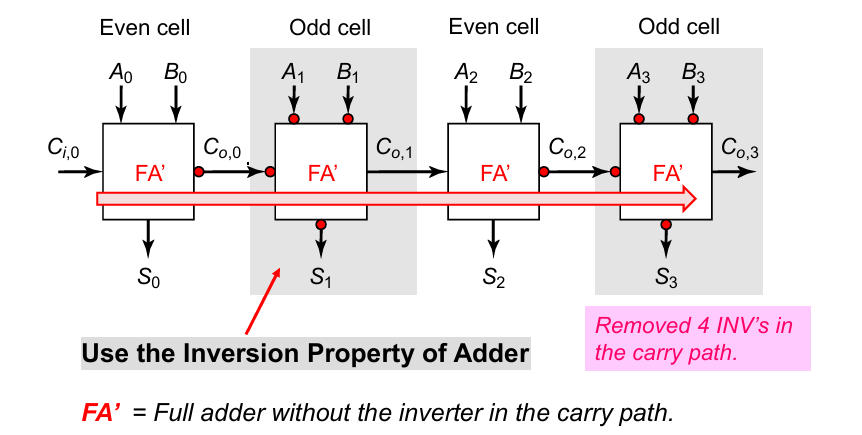
曼彻斯特进位链加法器

(待补充)

旁路进位加法器

旁路进位加法器的思路很简单：

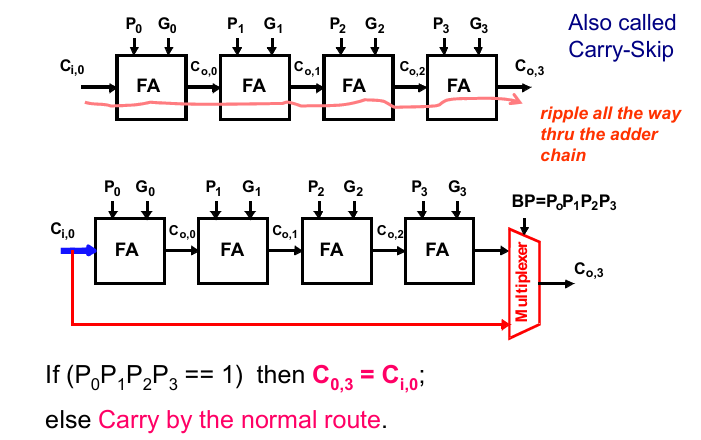
通过计算进位是否可以向下传递，通过添加一个Mux提前算出进位结果。

最坏情况下的关键路径如下：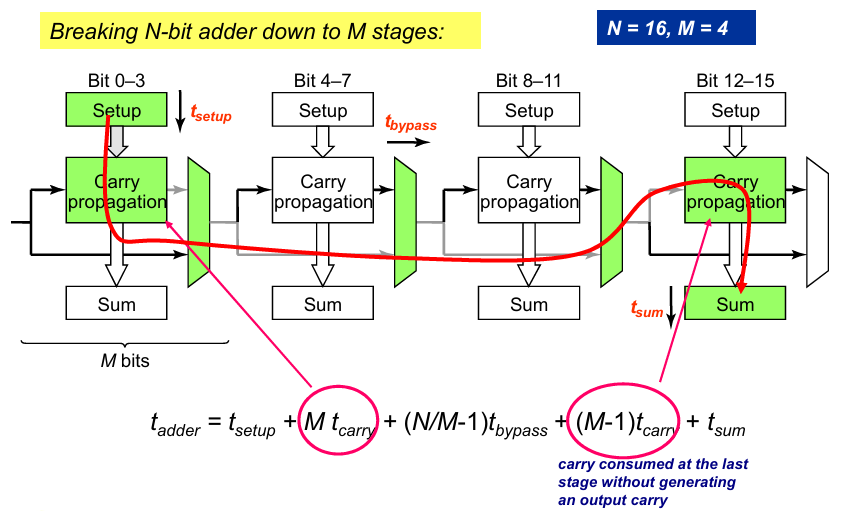

和行波进位加法器一样，旁路进位加法器的延迟与位数也是线性关系的：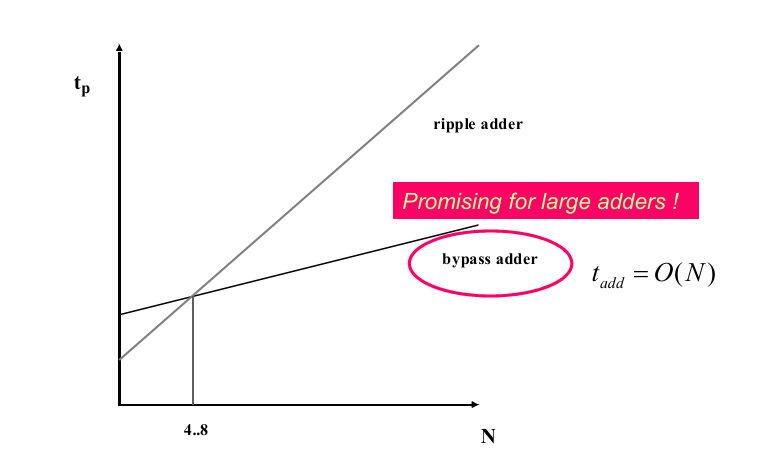

进位选择加法器

进位选择加法器的思路是，提前计算carry=0和carry=1的2种结果，通过传入的carry来选择最终的输出。

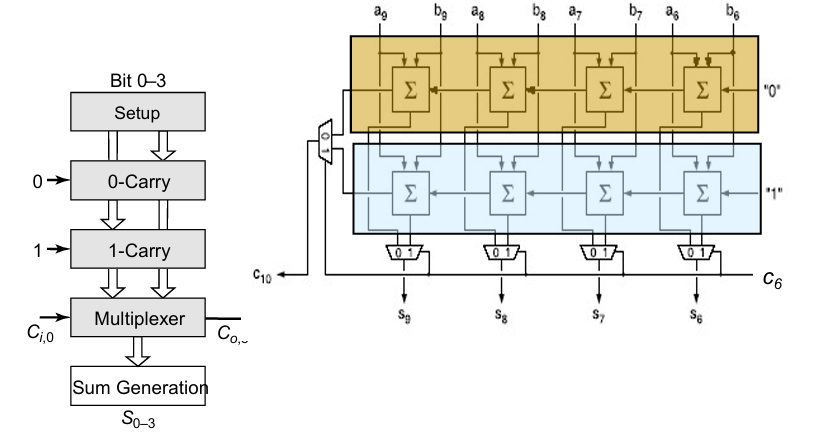
平分各个级数时：

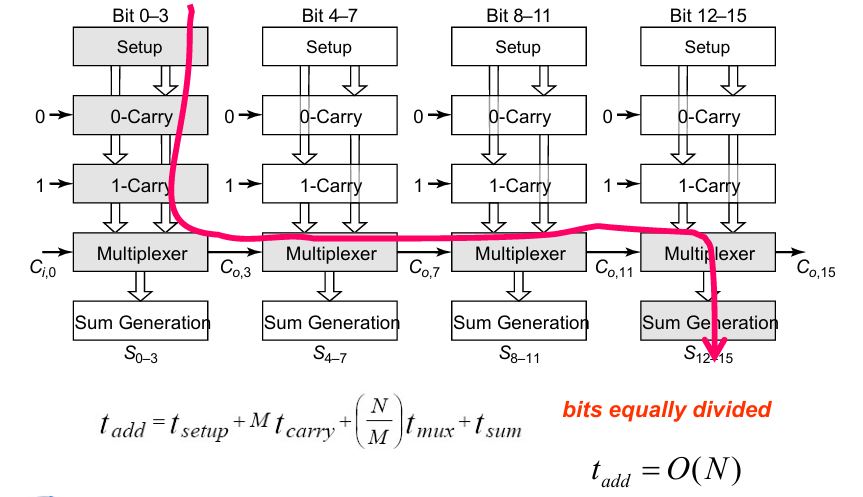
也可以按照平方的形式划分：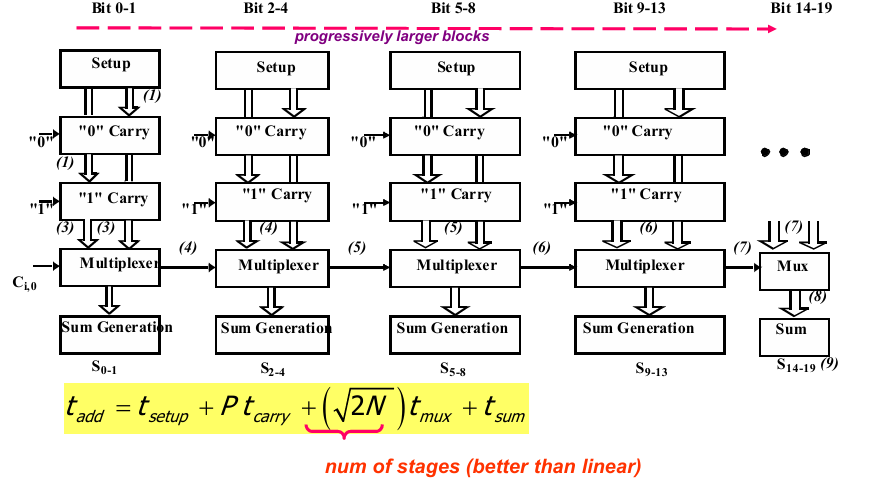

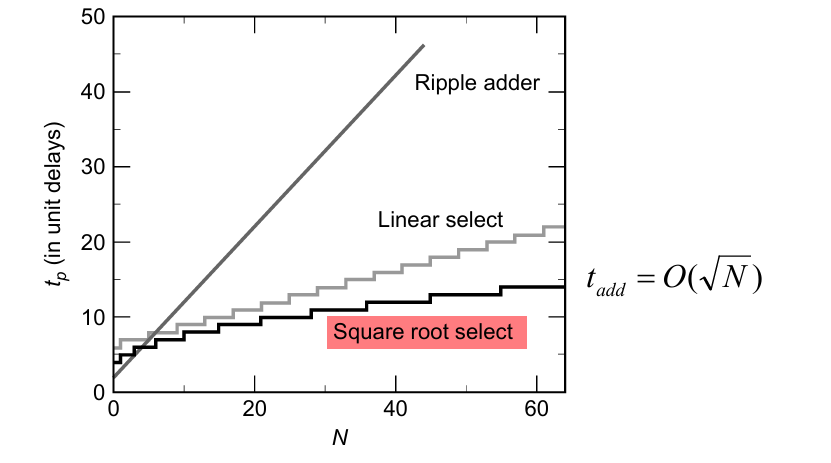
对于位数更高的加法器优化效果更好。

超前进位加法器

基础理论

加法器本质是组合逻辑，只要知道各位输入和进位输入，就可以得到进位输出。

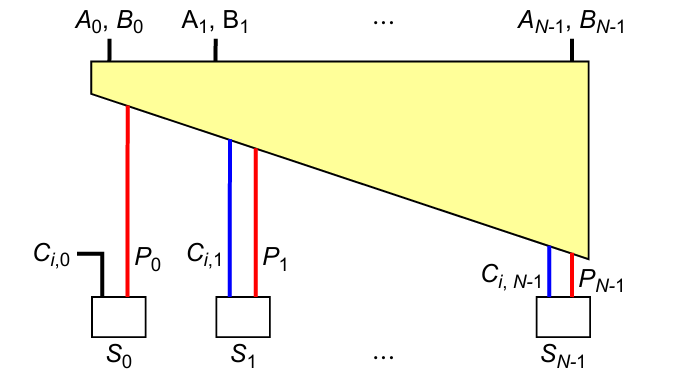
考虑第K位的进位输出：
$$C_{o,k} = f(A_k,B_k,C_{o,k-1}) = G_k+P_kC_{o,k-1}$$

即：第K位的进位产生有2种可能，一种是直接在第K位产生，另一种是低位产生的进位经由第K位传播。

注意到上面的$C_{o,k}$是一个迭代公式，可以一直迭代到最低位：

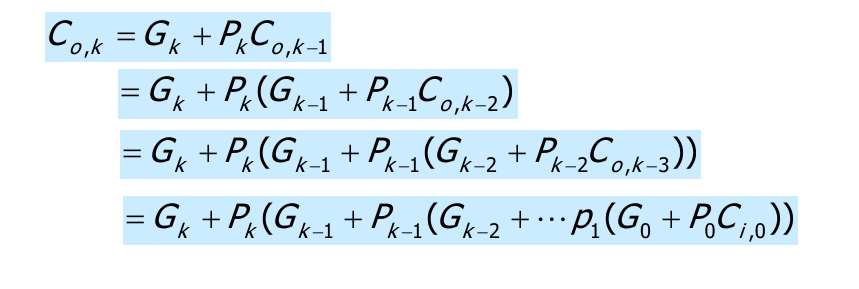
Lookahead Mirror

上面的公式可以通过下面的结构来实现：

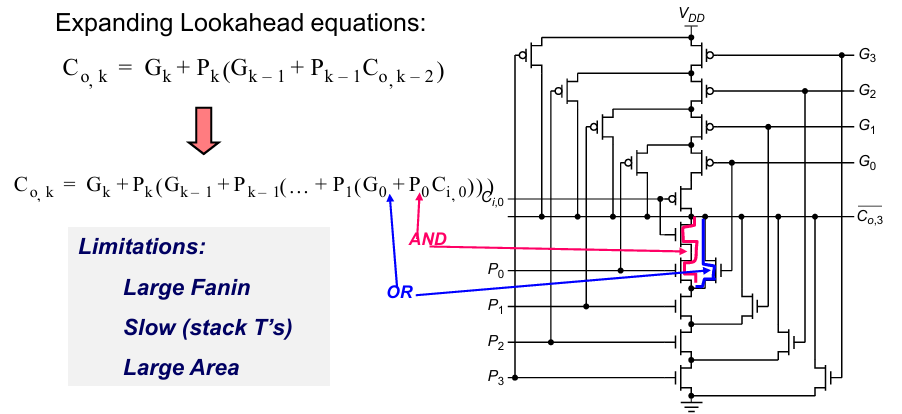
这个结构的问题在于虽然实现起来比较直观，但是扇入很大，位数一高延迟也很大。

块进位

重新组合进位传播公式，我们可以发现，如果将中间的几位看作一个整体，可以从块进位和块传播的角度理解进位公式。

其中
$P_{i:j}$表示产生的进位可以经由加法器的第i到j位传播，即：
$$P_{i,j} = P_iP_{i-1}P_{i-2}\cdots P_j$$

$G_{i:j}$表示在加法器的第i到j位这个区间能够产生进位。显然有多种可能：
$$G_{i:j}=G_i+ P_iG_{i-1:j} = G_i+P_i(G_{i-1}+P_{i-1}G_{i-2:j})=G_{i,k}+G_{k-1,j}P_{i,k}$$

定义一种新的算子：

$$(G,P)\bullet(G’,P’)=(G+PG’,PP’)$$

例如要计算
$$(G_{3:2},P_{3:2})\bullet (G_{1:0},P_{1:0})\
=(G_{3:2}+P_{3:2}G_{1:0},P_{3:2}P_{1:0})\
=(G_{3:0},P_{3:0})$$

新算子$\bullet$能够将2个区间的进位产生和进位传播连接起来。其输入为4，输出为2，计算了一个乘加和一个与操作。

通过这个算子，我们可以自由组合控制进位的传播：

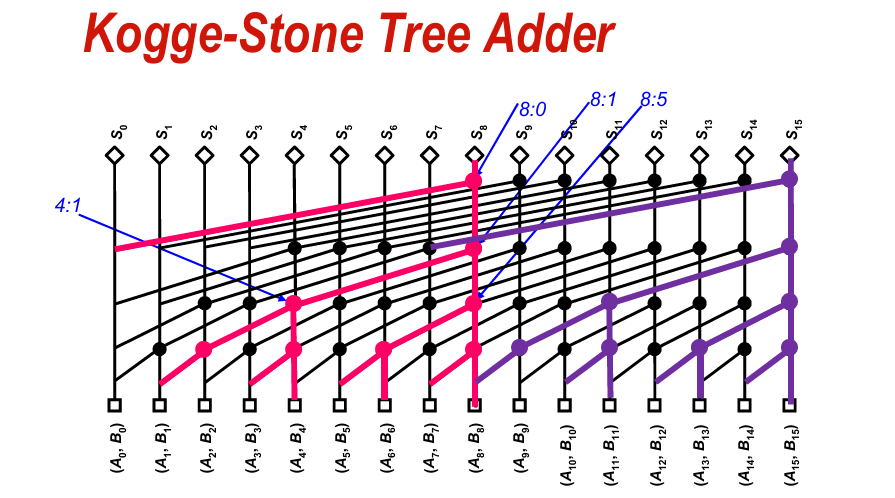
从而得到这样的树形加法器。

图中相邻2位的P和G产生过程如下：

$$(G_{1:0},P_{1:0}) = (G_{1:1},P_{1:1})\bullet (G_{0:0},P_{0:0})\
=(A_1B_1,A_1\oplus B_1)\bullet (A_0B_0,A_0\oplus B_0)$$

乘法器

二进制乘法器的原理可以表示为：

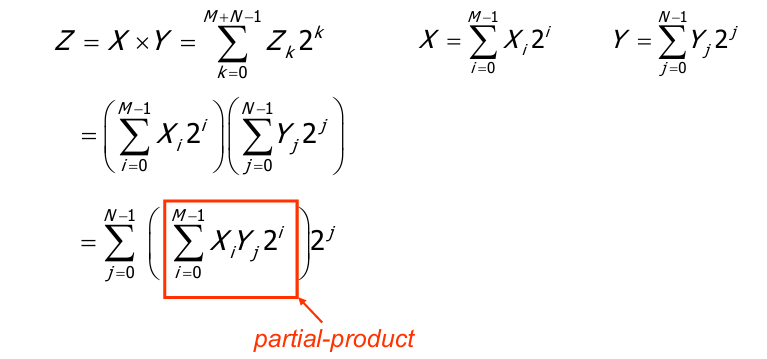
即我们熟悉的部分积之和的形式：

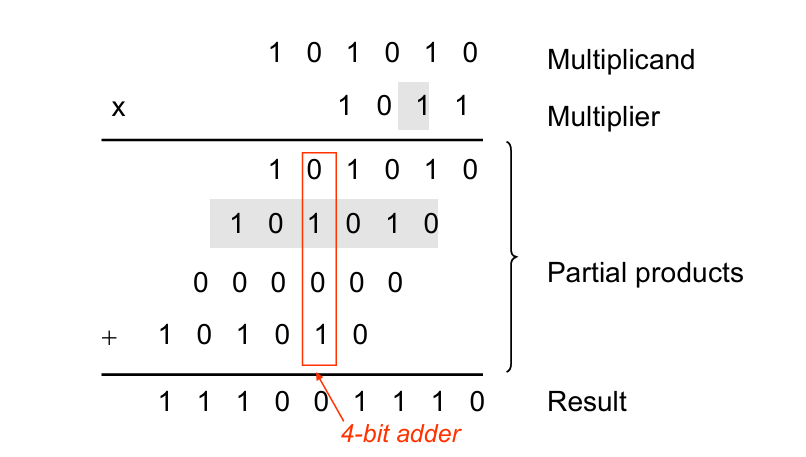
一般的乘法器可以做出下面的加法器阵列的形式。问题在于关键路径需要考虑多种进位情况。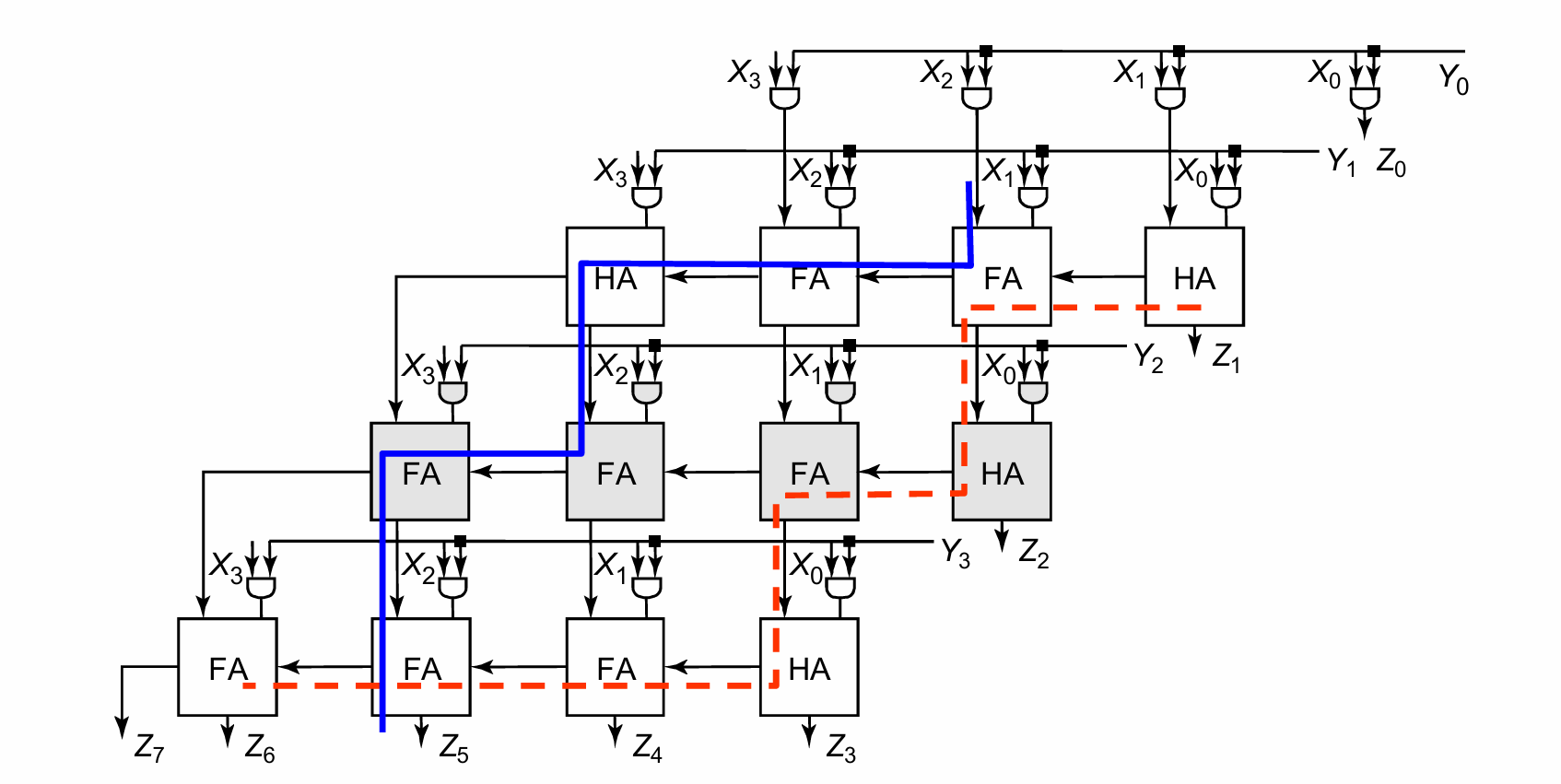

一种优化思路是进行对角线形式的进位，缩短关键路径：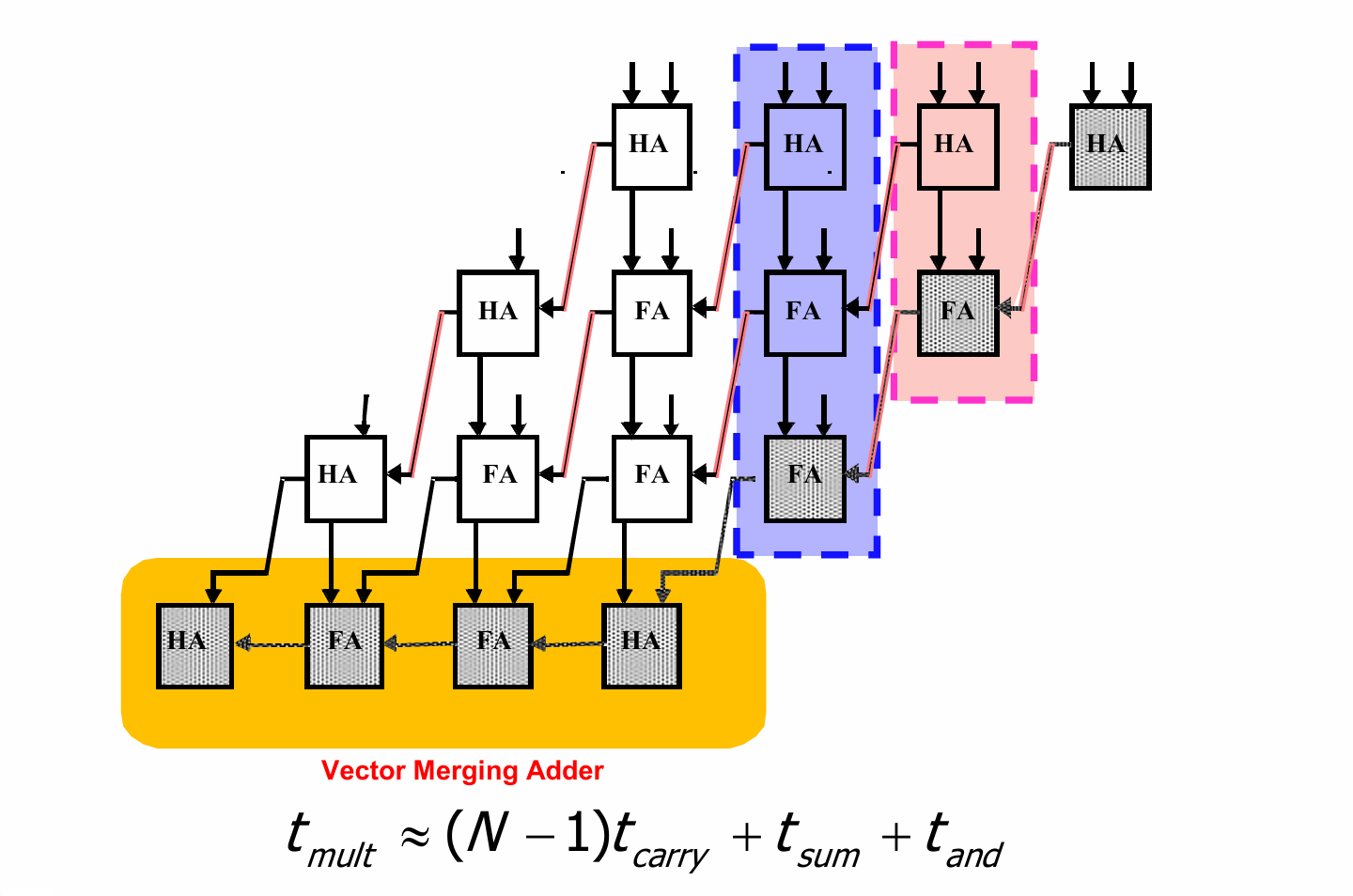

Wallace-Tree 乘法器

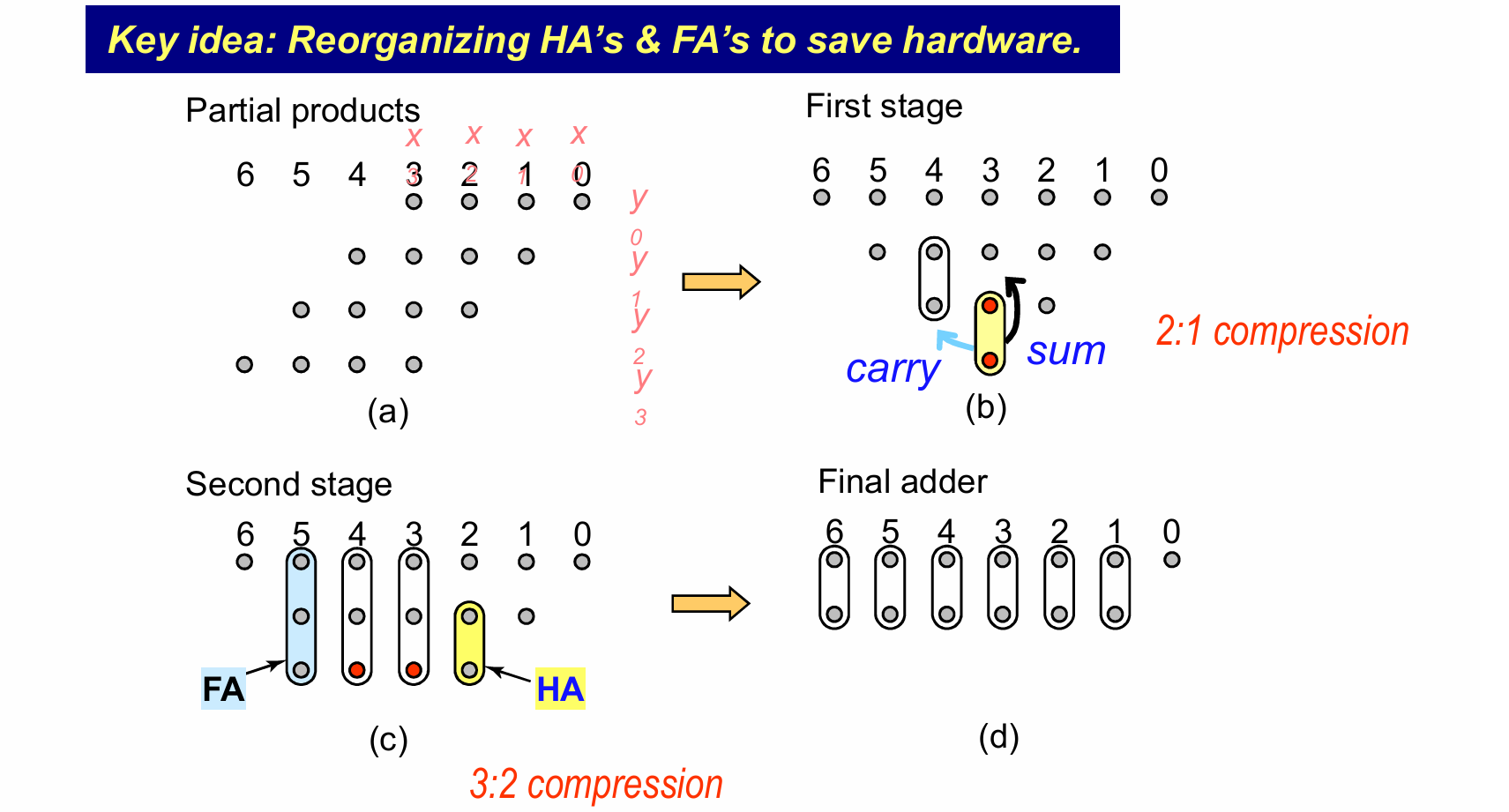
核心思路在于，半加器相当于2-2压缩器，全加器相当于3-2压缩器，通过重新排列全加器和半加器的位置，优化关键路径。