花间一壶酒

举杯邀明月，对影成三人

0%

数字IC八股

发表于 更新于
本文字数： 32k 阅读时长 ≈ 58 分钟
梳理一些数字IC面试的高频常见问题，以及一些手撕代码的题目。

数字电路设计基础知识

参考文献：
上海交通大学《SoC设计基础》，《高等数字集成电路设计》课程
《Digital logic RTL and Verilog Interview questions》

数字IC设计流程

SPEC定义->建模仿真->前端设计->仿真验证->逻辑综合->STA检查 (前端)

后端：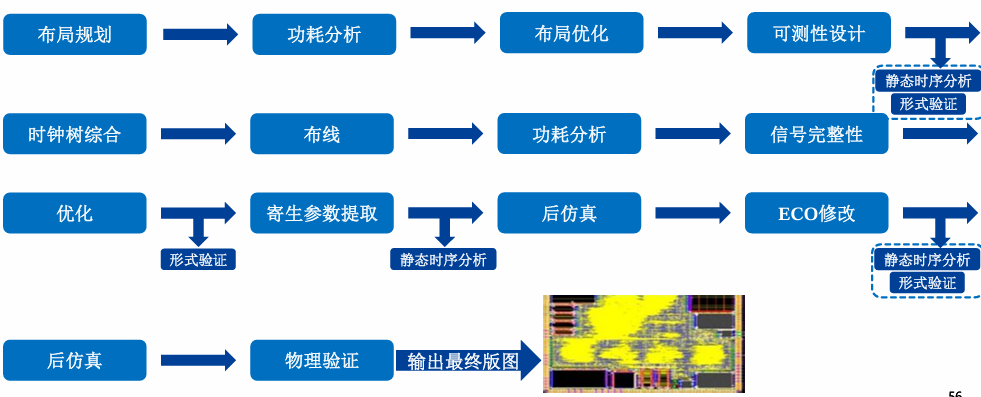

设计流程中的一些概念

  1. simulation和emulation
    • Simulation（仿真）：
      主要应用于设计的早期阶段，如逻辑设计、模块设计等。在设计的初步阶段，通过仿真来验证设计的基本逻辑功能，发现并修复逻辑错误。
      也用于验证设计的修改和优化，例如在对设计进行性能优化后，通过仿真验证优化是否达到了预期的效果。
    • Emulation（仿真验证）：
      通常应用于设计的后期阶段，如系统集成、验证等。在设计基本完成并且逻辑功能已经通过仿真验证后，使用仿真验证来验证设计在实际硬件环境下的性能和功能。
      也用于验证设计与外部设备的交互，例如验证芯片与内存、处理器等其他硬件组件的接口是否兼容。
    • Simulation（仿真）：
      使用软件模拟器来运行设计的模型。这些模拟器通常基于硬件描述语言（HDL）的代码，按照一定的仿真算法来模拟电路的行为。
      仿真过程是在计算机上运行的，不需要实际的硬件设备。可以通过编写测试激励（testbench）来驱动设计的输入，并观察输出结果。
    • Emulation（仿真验证）：
      使用硬件仿真器，通常是基于FPGA（现场可编程门阵列）或其他专用硬件平台。将设计映射到这些硬件平台上，以接近实际硬件的速度运行。
      需要将设计转换为适合硬件仿真器的格式，并进行一定的配置和调试。可以通过实际的硬件接口与外部设备进行交互，以验证设计在实际环境下的功能。
    • Simulation（仿真）：
      速度相对较慢，尤其是对于复杂的大型设计。因为仿真需要在软件中逐条执行HDL代码，模拟电路的每一个逻辑状态变化。
      但可以提供非常详细的调试信息，例如可以查看任意信号在任意时间点的值，可以设置断点、观察波形等。
    • Emulation（仿真验证）：
      速度比仿真快得多，可以接近实际硬件的运行速度。因为它是基于硬件平台运行的，能够以较高的频率执行设计。
      但调试信息相对较少，通常只能观察到接口信号和一些关键信号的值，难以像仿真那样查看内部的详细逻辑状态。

一句话总结：simulation是纯软件仿真，emulation需要使用硬件模拟。根据软硬件的特性从而有了不同效果。
本文倾向于将simulation翻译为仿真，emulation翻译为模拟。

时钟与同步

同步电路中，用一个电路来处理各个部分的操作。所有触发器都可以认为只与一个时钟有关(频率和相位可以不同，但是会有确定的关系)
异步电路中，系统没有统一的时钟信号。在这种电路中，每个模块可以在准备好时开始和结束操作，而不需要等待一个全局的时钟脉冲。这使得异步电路可以在某些情况下实现更高的效率和更低的功耗，因为它们仅在需要时消耗能量执行任务。然而，异步电路的设计复杂度更高，测试和验证也更加困难，因为没有统一的时间基准来确保操作的一致性和正确性。
同步与异步电路的优缺点比较如下图：

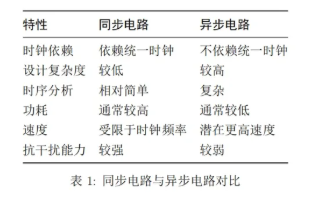
alt text

同步复位和异步复位

在同步复位中，复位操作只有在时钟的有效边沿（上升沿或下降沿）到来时才会生效。
同步复位的优点：复位信号被视为数据信号处理，因此可以更好地过滤掉复位信号上的毛刺（短暂的、非预期的信号变化），提高系统的稳定性。更容易进行时序分析和验证。
缺点：如果系统时钟出现问题（例如由于噪声导致时钟丢失），则可能无法正确地执行复位操作，可能导致系统进入不一致的状态。

异步复位电路的复位操作在任何时间都可以生效。
优点：

  • 提供了快速且确定性的复位机制，无论时钟状态如何，都能保证电路迅速进入初始状态。
  • 在时钟不稳定或不存在的情况下，仍能确保电路安全复位。
    缺点：
  • 对复位信号上的毛刺较为敏感，可能会因为毛刺而意外触发复位，从而影响系统的稳定性。
  • 设计复杂度较高，尤其是在需要考虑复位释放后的同步问题时，以避免亚稳态问题。

异步复位同步释放

异步复位：复位操作的置位不受时钟影响，只要对应的复位信号有效，就能将电路复位。
同步释放：复位信号的取消必须和时钟信号的边沿同步。

异步复位同步释放结合了异步复位和同步复位的优点，即在与时钟无关的情况下对寄存器进行复位，同时避免了亚稳态问题。
一个异步复位同步释放的例子如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
module async_rst_n(
input clk,
input rst_n,
input d,
output reg dout
 );
 
//*************code***********//
 
reg rst_n_sync;
reg rst_reg;
 
always @(posedge clk or negedge rst_n_sync) begin
    if(!rst_n_sync)begin
        dout <= 1'b0;
    end
    else begin
        dout <=d;
    end
end
 
always @(posedge clk or negedge rst_n)begin
    if(!rst_n)begin
        rst_reg <= 1'b0;
        rst_n_sync <= 1'b0;
    end
    else begin
        rst_reg <= 1'b1;
        rst_n_sync <= rst_reg;
    end
end
 
//*************code***********//
endmodule

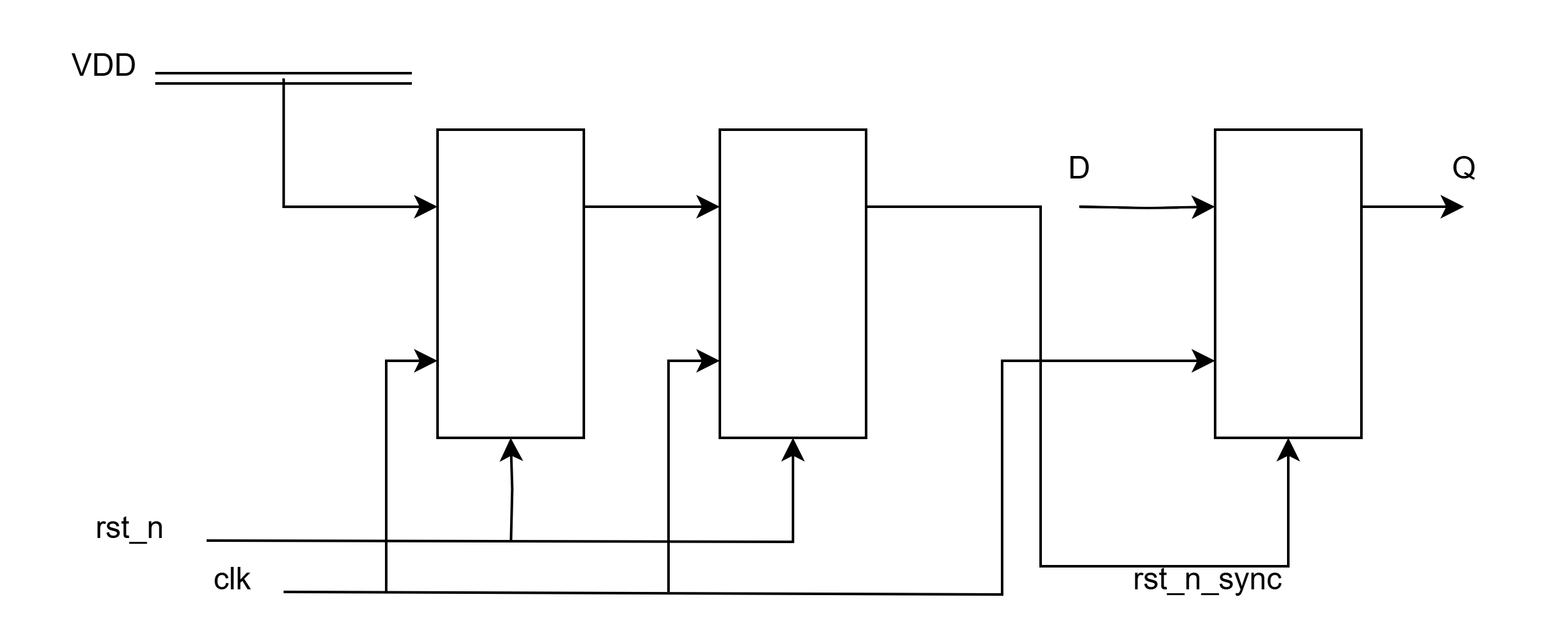
alt text

异步复位信号直接复位两级synchronizer，通过寄存器输出间接复位data寄存器,这样当解复位时，data 1通过2级寄存器同步后进行解复位。

静态时序分析

Setup time

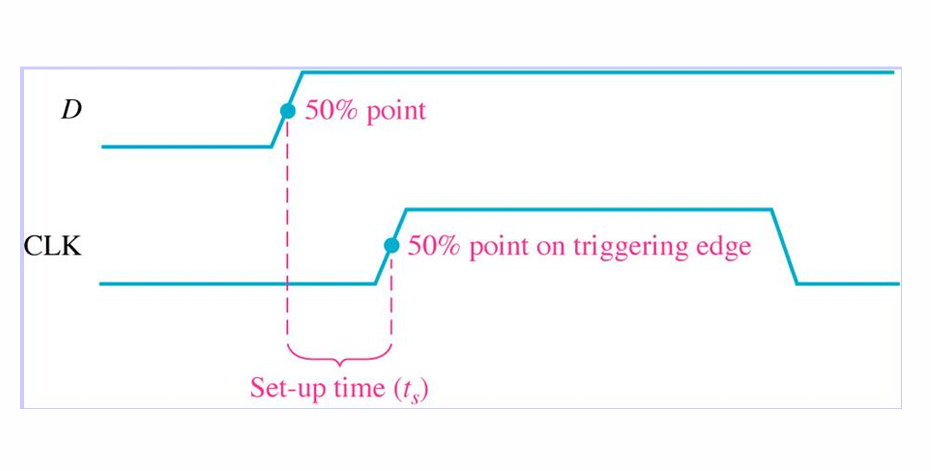
alt text
在时钟驱动沿(一般是上升沿)到来前，数据需要提前一段时间准备好，这个时间称为建立时间。

Hold time

时钟驱动沿到来后，数据需要保持不变让寄存器完成采样所需要的时间。

SDC约束

一个典型的SDC文件会按以下顺序组织：

设计环境设置 (set_operating_conditions, set_wire_load_model 等)
时钟定义 (create_clock, create_generated_clock)
I/O 约束 (set_input_delay, set_output_delay, set_driving_cell, set_load)
时序例外 (set_clock_groups, set_false_path, set_multicycle_path)
设计规则约束 (set_max_transition, set_max_capacitance, set_max_fanout)

Multicycle Path

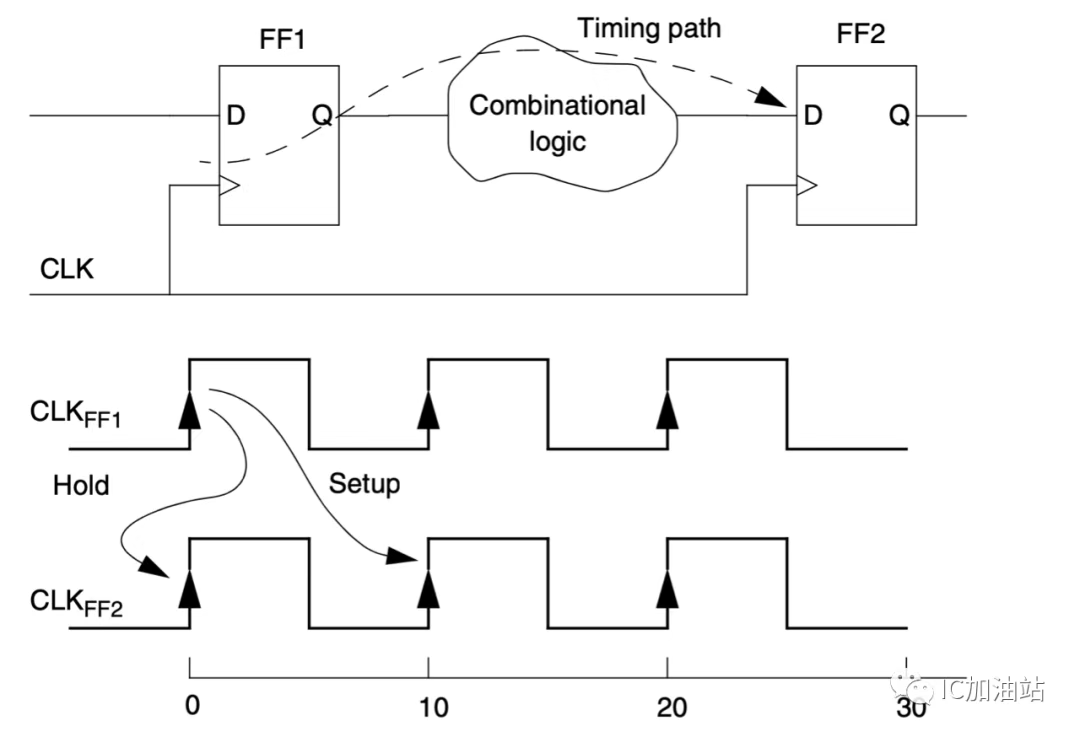
在多数电路中，2级Flip Flop之间的组合逻辑经由一个周期的时长就能完成计算稳定下来。如上图中，0时刻FF1的Q端变化，10时刻前，FF2的D端达到稳定(建立时间)，之后10时刻，FF2的Q端对D进行采样。


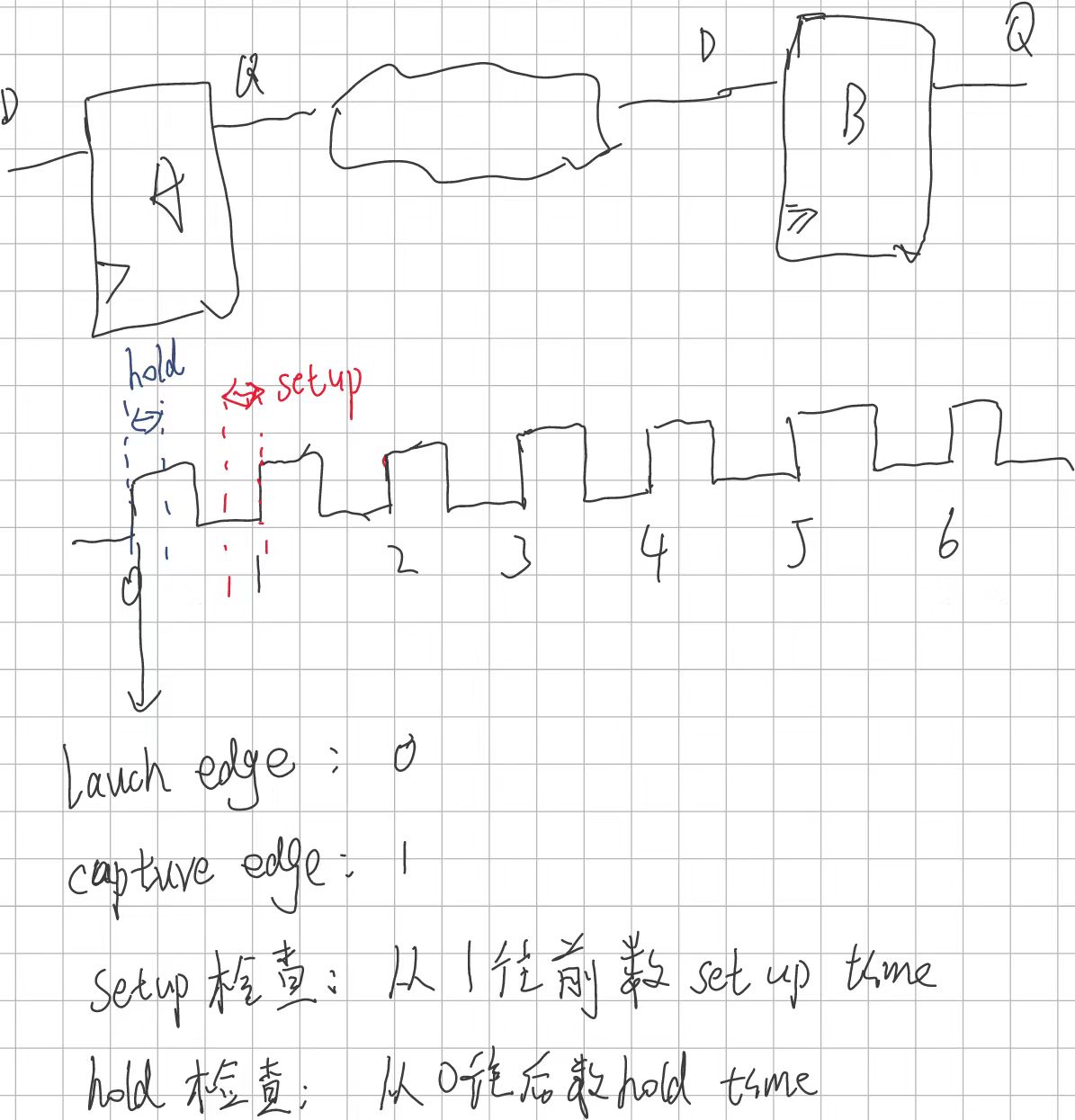
启动边沿 (Launch Edge): 数据从源寄存器 (regA) 被送出的时钟边沿（例如 T=0ns）。

捕获边沿 (Capture Edge): 目标寄存器 (regB) 试图捕获数据的时钟边沿。
默认行为 (单周期路径):
建立检查 (Setup): 检查数据在下一个捕获边沿（T=10ns）之前是否稳定。
保持检查 (Hold): 检查在同一个启动边沿之后，数据是否足够晚才到达，以避免破坏前一个周期（在 T=0ns）刚刚捕获的数据。参考点是 T=0ns。

如果是multicycle path,希望组合逻辑在2个周期完成运算，如下图：

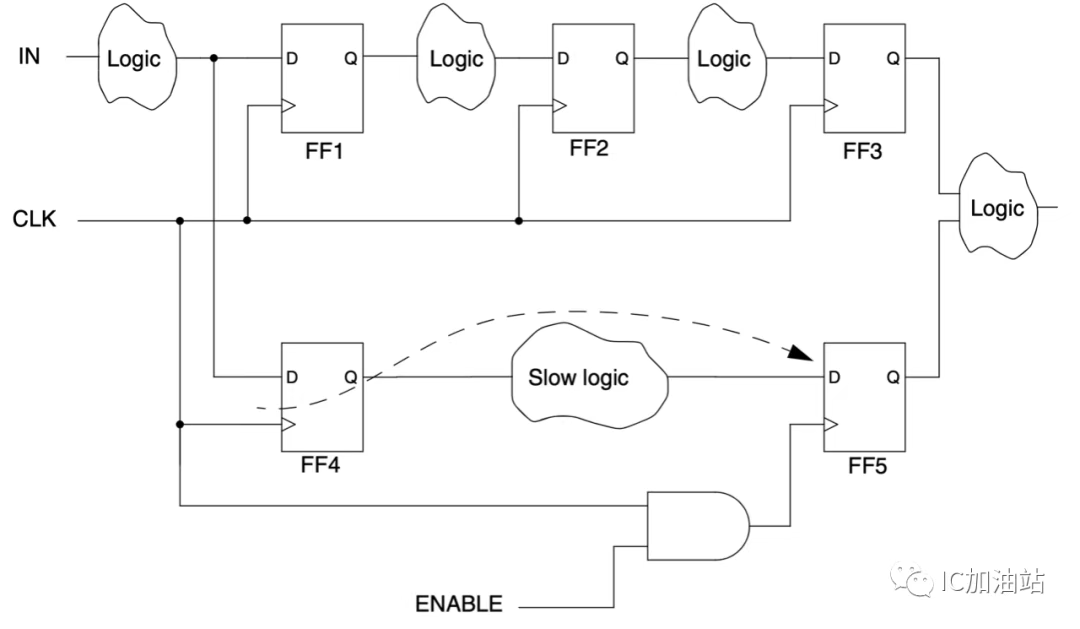
希望FF4的Q端变化经过2个cycle后才被FF5采到，那么就需要设置multicycle path,其基本语法如下：

1
2
3
4
set_multicycle_path path_multiplier [-setup|-hold]   
                  [-start|-end]                     -from <StartPoint>     
                  -through<ThroughPoint>                  
                  -to <EndPoint>

可以写成：

1
2
3
4
5
6
7
8
9
10
11
# 设置多周期路径：数据从 regA 到 regB 需要 2 个周期
set_multicycle_path -setup 2 \
                     -from [get_pins regA/Q] \
                     -to [get_pins regB/D]

# 设置相应的保持时间约束
# 因为 setup 是 2，所以 hold 应该是 2-1 = 1
# 这表示保持时间检查从原来的 (launch_edge + 0) 移动到 (launch_edge + 1)
set_multicycle_path -hold 1 \
                     -from [get_pins regA/Q] \
                     -to [get_pins regB/D]

效果:
建立检查: 在 regA 的时钟上升沿 T=0ns 捕获数据，在 regB 的时钟上升沿 T=20ns (第3个边沿) 检查数据是否稳定。允许的最大延迟为 20ns。
保持检查: 检查 regA 在 T=0ns 发出的数据，不会破坏 regB 在 T=10ns (第2个边沿) 刚刚捕获的旧数据。检查点在 T=10ns。

跨时钟域传输

参考：
《Clock Domain Crossing (CDC) Design & Verification Techniques Using SystemVerilog》

亚稳态的概念

要完全理解亚稳态问题，需要回到集成电路中数据存储的方式中来，如下图所示：

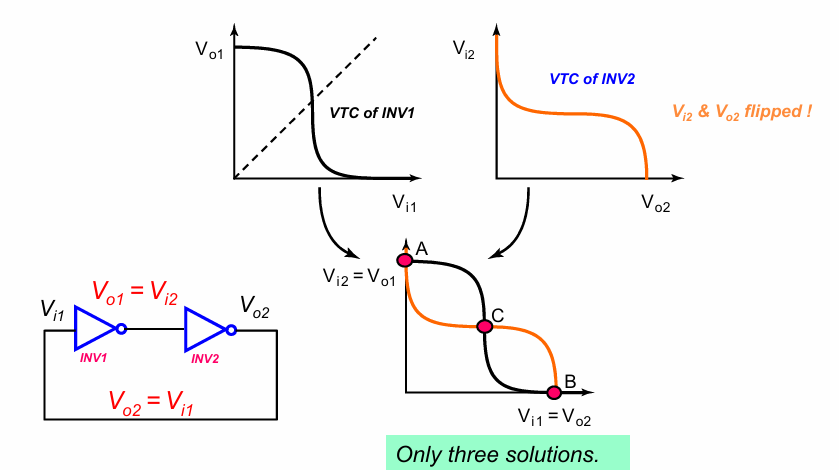
电路中，低电平代表0，高电平代表1，想要一个电路能够存储0或1，自然想到需要构造一种电路，能够稳定在低电平或高电平，即，构造一种双稳态电路。2个反相器相连，则构成了一种最简单的双稳态电路,简单分析一下，容易得到如上图中的电压关系曲线，即著名的蝶形曲线。
这个蝶形关系意味着，关于2个反相器的输出电压$V_{o1}$，$V_{o2}$有3种可能的解，分别对应图中的A,B,C点，并且解A,B对应的状态是很稳定的，如下图所示：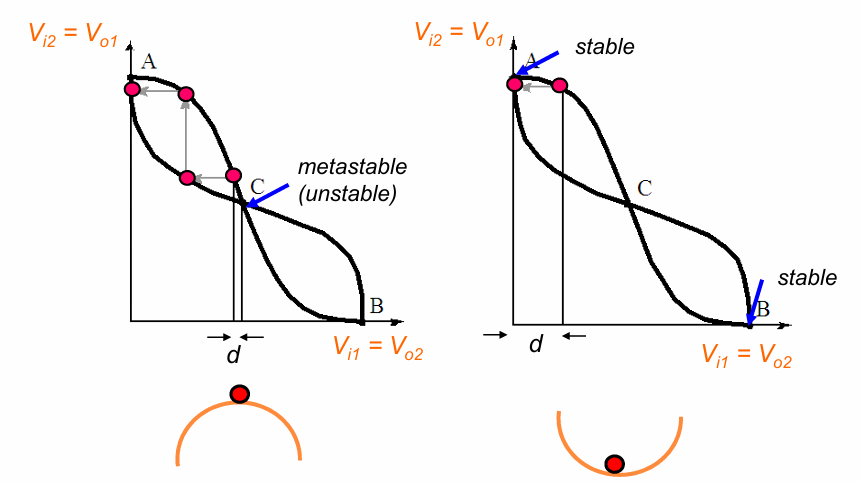
alt text
如果某个时刻电路处于左图中红点的位置，即相对于C产生了某种震荡，则电路自身的反馈效应会将电压拉到A点，并维持稳定。

但是，这不意味着解C不存在，只是相等于A和B来说，C这个解并不稳定。处于C状态的电路，随时有可能变成A或B，但究竟是变成A还是变成B，什么时候变，都是不确定的。因此我们将C这个状态称为亚稳态。

我们分析一个如图所示的D Flip Flop: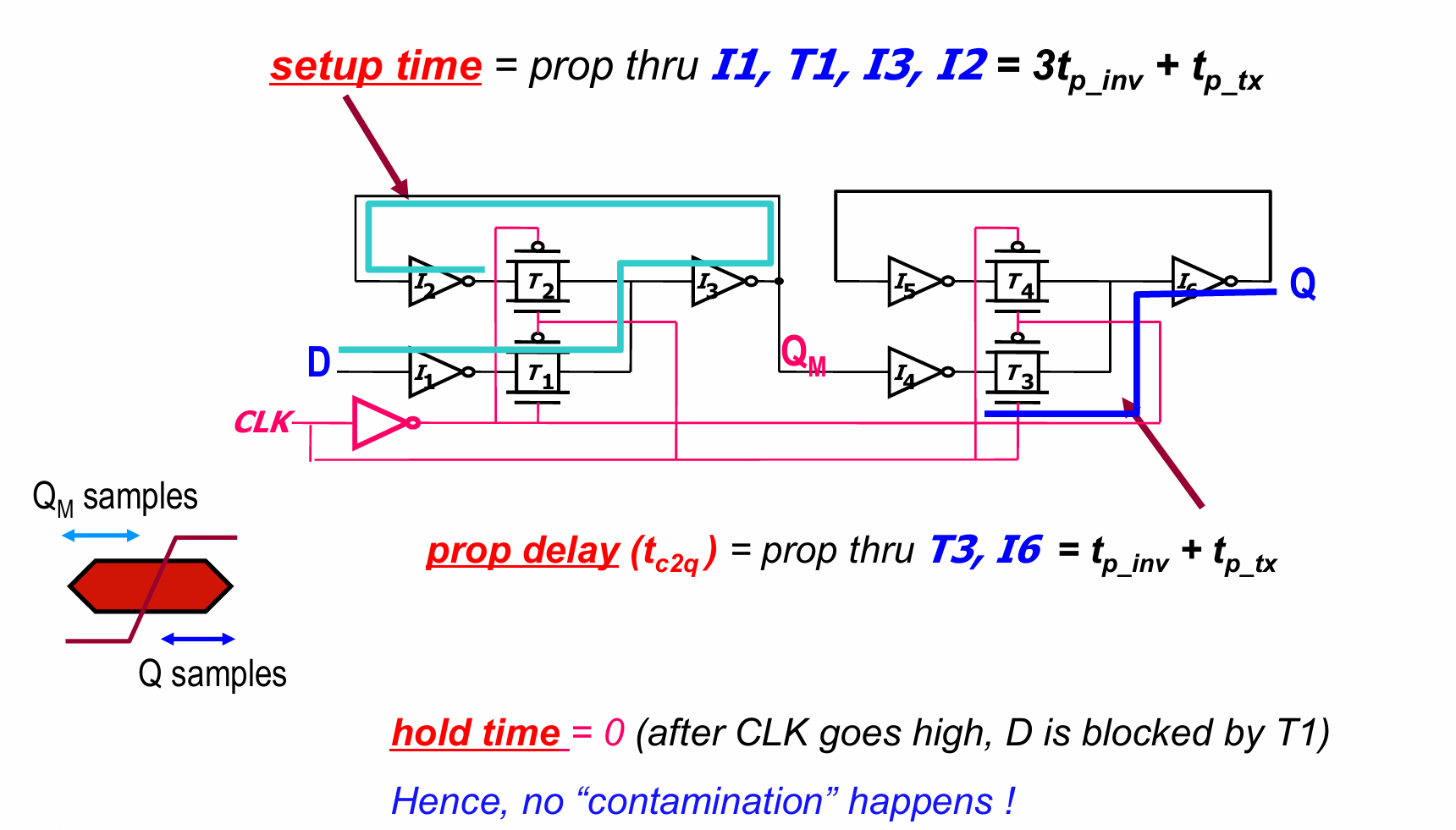
alt text

这是一个由2级Latch组成的寄存器，Latch是电平有效的，对第一级Latch,CLK为0时置位此时T1的传输管打开，有$Q_M=D$。左边的电路要保持稳定，信号的传输路径为$I_1,T_1,I3,I2$。当clk上升沿到来，即clk由0变1时，T3打开，$Q=Q_M$。传输延迟为$T_3,I_6$

由于建立时间的定义为:时钟上升沿到来前，数据需要提前准备好的时间。经过分析可以得到，上述电路的建立时间为$3t_{p_inv}+t_{p_tx}$

图中分析的hold time=0其实不准确，事实上hold time应当等于第一个传输门$T_1$关闭所需要的时间。在这个期间内，信号D的值需要保持稳定。

如果信号D的变化不满足上述建立时间和保持时间，在Q端就可能产生亚稳态。

需要指出的是，亚稳态的产生无法消除，仅能尽量避免。亚稳态的产生是一个概率事件。只需要保证MTBF(Mean Time Between Failure)大于某个阈值，芯片就是可用的。

单Bit跨时钟域传输

单bit的跨时钟域传输，一般采用2级寄存器，即double flop synchronizer的方式，如下图：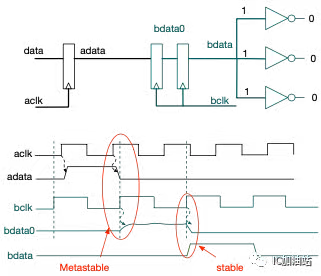

根据前面对亚稳态的分析可以知道，双稳态电路中的亚稳态一定可以稳定下来，只是需要时间，而这个时间窗口在绝大部分情况下小于一个bclk cycle。
如上述波形图所示，第一个cycle周期的前半段，信号bdata0的质量不稳定，但是当第二个bclk上升沿到来时，能够采样到稳定的bdata0，从而消除了亚稳态。

对于一级寄存器，其亚稳态的MTBF计算如下。

当2级寄存器级联时，公式变为：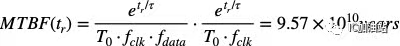

这个时间足够长，一般大于数千年乃至数亿年，因此我们可以认为避免了亚稳态产生。

同时，需要注意的是，跨时钟域传输对信号的持续时间有要求。如下图：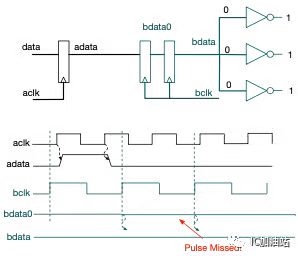

如果adata持续时间小于1个bclk cycle，则可能导致采样失败。这要求source data必须保证稳定不变至少碰见destination clock 3个连续的沿，这个沿可以是上升沿也可以是下降沿，持续3个沿之后才能变，否则就有可能在destination clock domain根本看不到这个data的变化。
如果bclk的频率是1.5倍的aclk频率以上，即使adata是aclk域的一个短pulse，也可以保证3edge要求。

脉冲同步

在上图中，adata实际上是aclk时钟域的一个脉冲信号。在数字电路中，我们有时候希望脉冲信号在被同步后仍然是一个脉冲信号。这要求实现一个脉冲信号的跨时钟域同步。其原理如下：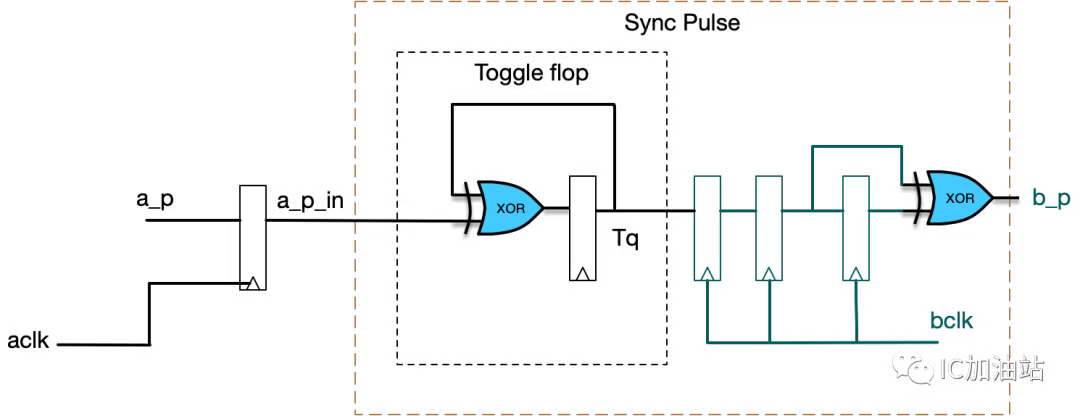

图中的Toggle flop能够将一个脉冲信号转换为电平信号，经过2级跨时钟同步后，在用一个异或门将电平信号转换为脉冲信号。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
`timescale 1ns/1ns

module pulse_detect(
	input 				clk_fast	, 
	input 				clk_slow	,   
	input 				rst_n		,
	input				data_in		,

	output  		 	dataout
);

	reg toggle_flop;
	reg d1,d2,d3;
	always @(posedge clk_fast or negedge rst_n)begin
		if(!rst_n)begin
			toggle_flop <= '0;
		end
		else begin
			toggle_flop <= toggle_flop ^ data_in;
		end
	end

	always @(posedge clk_slow or negedge rst_n)begin
		if(!rst_n)begin
			d1 <= '0;
			d2 <= '0;
			d3 <= '0;
		end
		else begin
			d1 <=toggle_flop;
			d2 <= d1;
			d3 <= d2;
		end
	end

	assign dataout = d3^d2;


endmodule

多bit跨时钟域传输

使用异步fifo。代码见电路部分。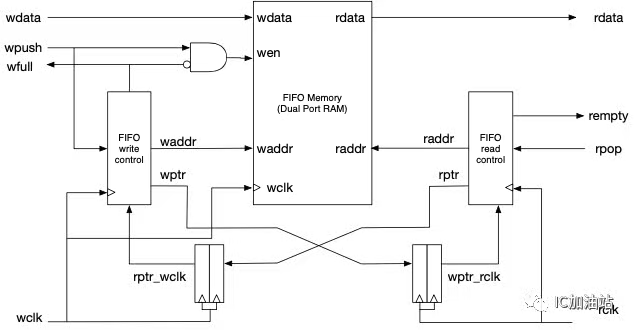

功耗

功耗类型及成因

alt text

动态功耗的构成主要是开关功耗和短路功耗。

开关功耗是指逻辑门进行电平翻转时，需要对器件中的电容进行充放电所消耗的能量。这个功耗可以通过如下公式计算：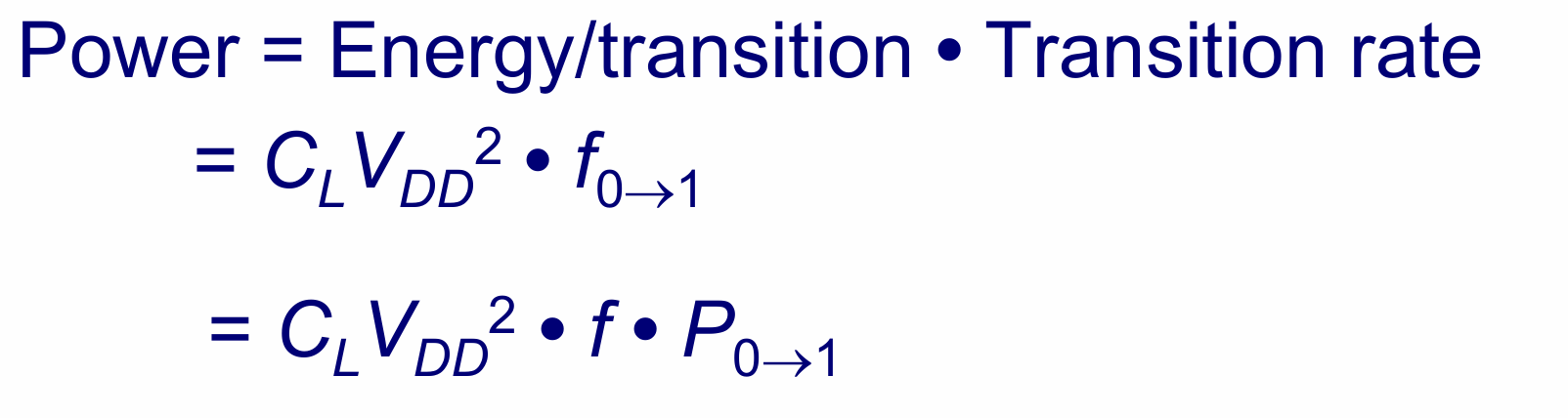

其中$C_L$为负载电容，$V_DD$是电源电压，f是电路频率，$P_{0->1}$是对应逻辑在每个cycle内的翻转概率。

短路功耗指的是在CMOS电路发生翻转的瞬间，P管和N管同时导通，此时存在一个持续时间极短的，从$V_{DD}$到$V_{SS}$的短路电流。

静态功耗是电路不发生翻转时产生的各类漏电。这是因为晶体管不是理想器件，存在各类效应产生了这样的漏电。

  1. 亚阈值漏电流 (Subthreshold Leakage):
    原理： 当MOS管处于关断状态（栅源电压 V_gs 低于阈值电压 V_th）时，源极和漏极之间仍存在微弱的电流。这是现代深亚微米和纳米级工艺中最主要的静态功耗来源。
    影响因素： 对阈值电压 V_th 非常敏感，V_th 越低，漏电流越大。工艺尺寸越小，短沟道效应越明显，亚阈值漏电流越严重。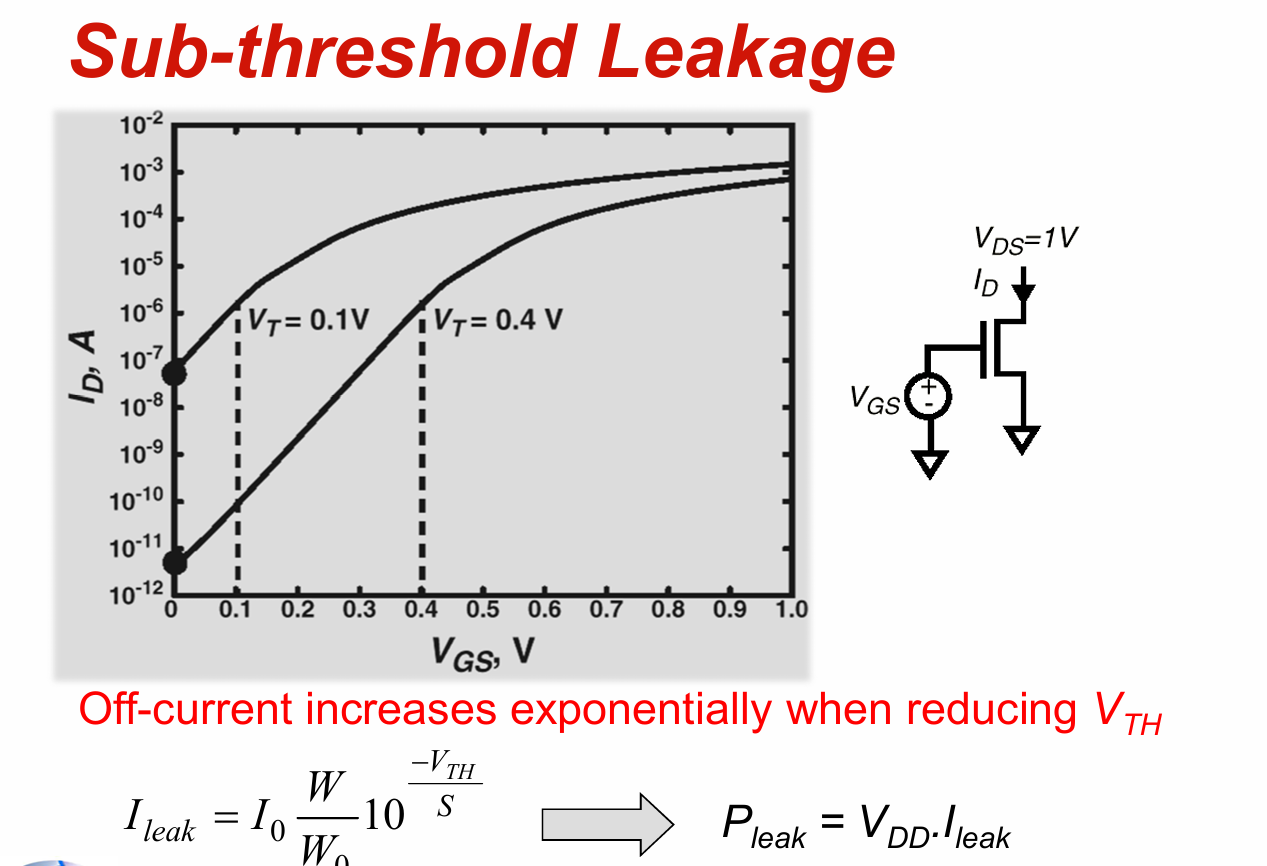

    这也是静态漏电的主要来源。

  2. 栅极漏电流 (Gate Leakage):
    原理： 由于栅氧化层变得极薄（尤其在45nm及以下工艺），电子可以通过量子隧穿效应穿过氧化层，从栅极流向沟道或反向流动。
    类型： 包括栅极到沟道的隧穿、栅极到源/漏的隧穿等。

  3. 结漏电流 (Junction Leakage):
    原理： 源/漏区与衬底形成的PN结在反向偏置时存在的微小漏电流，主要包括反向偏置PN结的饱和电流和隧穿电流。
    其他漏电流： 如栅诱导漏极降低（GIDL）等

低功耗设计

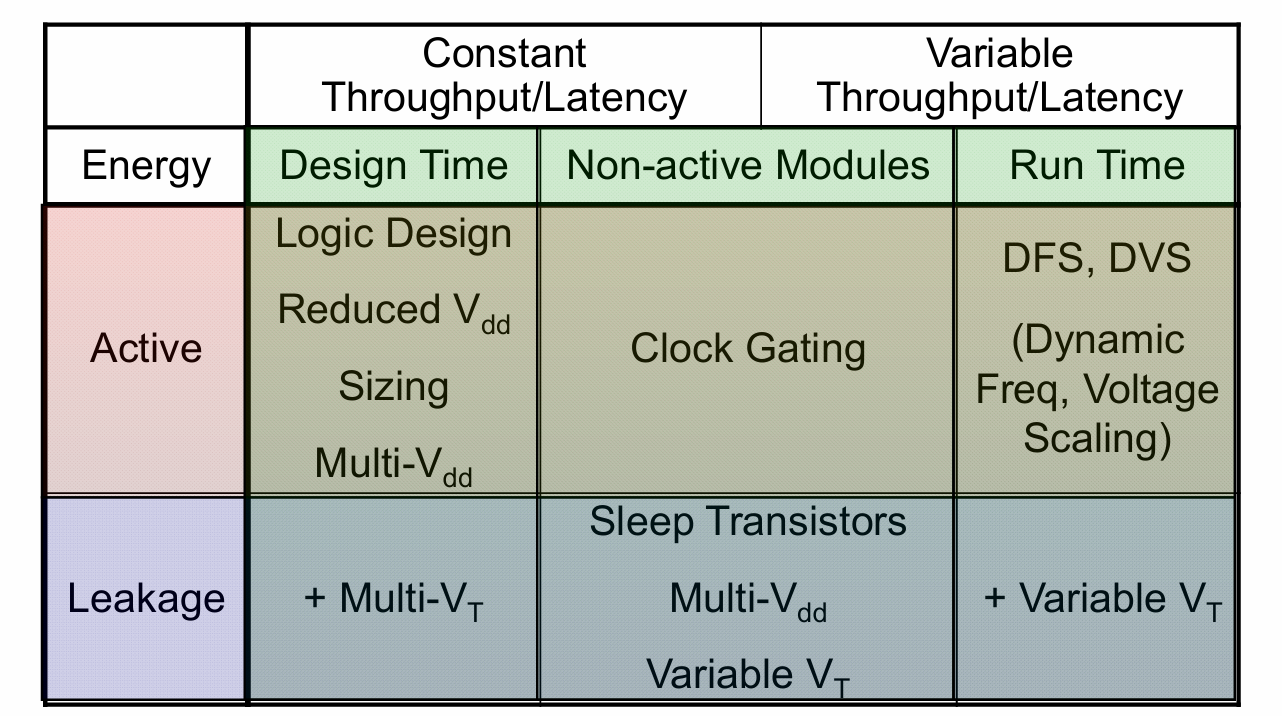
alt text

根据功耗来源的不同，可以针对性的制定各类低功耗设计方法，其设计矩阵如上图。

Active Design Time

根据动态功耗的公式我们可以知道，动态功耗和VDD的平方成正比。如果可以减小Vdd，自然可以降低功耗。多电压域的核心思想如下：

  1. 将非关键路径的电路移到更低的电压域
  2. 核心的，追求性能的电路使用高电压域，保证延迟和带宽

此外，也可以通过并行和流水线的方式，在满足设计需求的前提下，降低电压和电路频率，从而降低功耗。

在设计阶段，也可以考虑使用格雷姆和独热码进行状态机的编码，降低翻转频率。

Active Non-active Modules

此外，也可以考虑clock gating技术，在需要时，通过gate控制，关闭时序逻辑的时钟，让对应的组合逻辑不发生跳变。

rtl 设计层面，使用如下代码：

1
2
3
4
5
6
7
reg [3:0] state;
always @ (posedge clk or negedge nrst )begin
if (!nrst)
   state  <= 4'b0101;
else if (clk_en)
   state <= next_state;
end

通过添加一个clk_en信号，工具会综合出带有clock gating的Flip Flop单元。

clk gating单元本身也有很多种实现方式，基于与门(组合逻辑)的、基于Latch的和基于Flop的，需要视具体的工艺库决定。

Active Runtime

采用DVFS技术，即Dynamic Voltage Frequency Scaling，通过系统调度动态条件电压和频率，达到降低功耗的目的。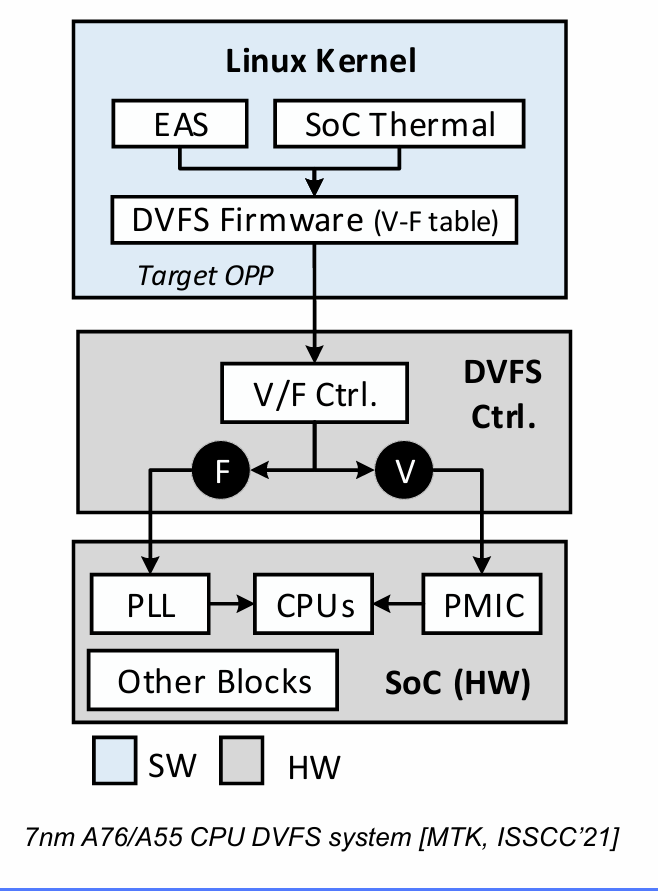

Leakage Design Time

对于静态功耗，大头是亚阈值漏电，因此可以在阈值电压上下功夫。使用多阈值电压技术：
方法：
高阈值电压 (High-Vt) 单元： 用于非关键路径上的逻辑门。它们开关速度慢，但漏电流极小。
低阈值电压 (Low-Vt) 单元： 用于时序关键路径上的逻辑门，以满足性能要求。它们速度快，但漏电流大。

Leakage Non-Active Module

电源门控 (Power Gating)
这是降低静态功耗最有效的方法之一，尤其适用于可以长时间处于空闲状态的模块。

原理： 在模块的电源（V_dd）或地（GND）路径上串联一个由高阈值电压（HVT）晶体管构成的“开关”（Power Switch）。当模块不工作时，关闭这个开关，将模块的电源或地断开，使其电压接近0，从而将漏电流降至几乎为零。
类型：

配套技术：

  1. 隔离单元 (Isolation Cells)： 在断电模块的输出端插入，防止其输出进入不确定状态而影响其他工作模块。
  2. 保持寄存器 (Retention Registers)： 对需要在断电后保留状态的关键寄存器，使用特殊寄存器，由常开电源（V_dd_always_on）供电。
    状态保持 (State Retention)： 在断电前将关键状态保存到保持寄存器或外部存储，上电后恢复。

优点： 静态功耗降低效果极佳（可接近零）。
缺点： 增加了面积（电源开关、隔离单元、保持寄存器）、上电/断电需要额外的控制逻辑和时间、存在“浪涌电流”（inrush current）问题。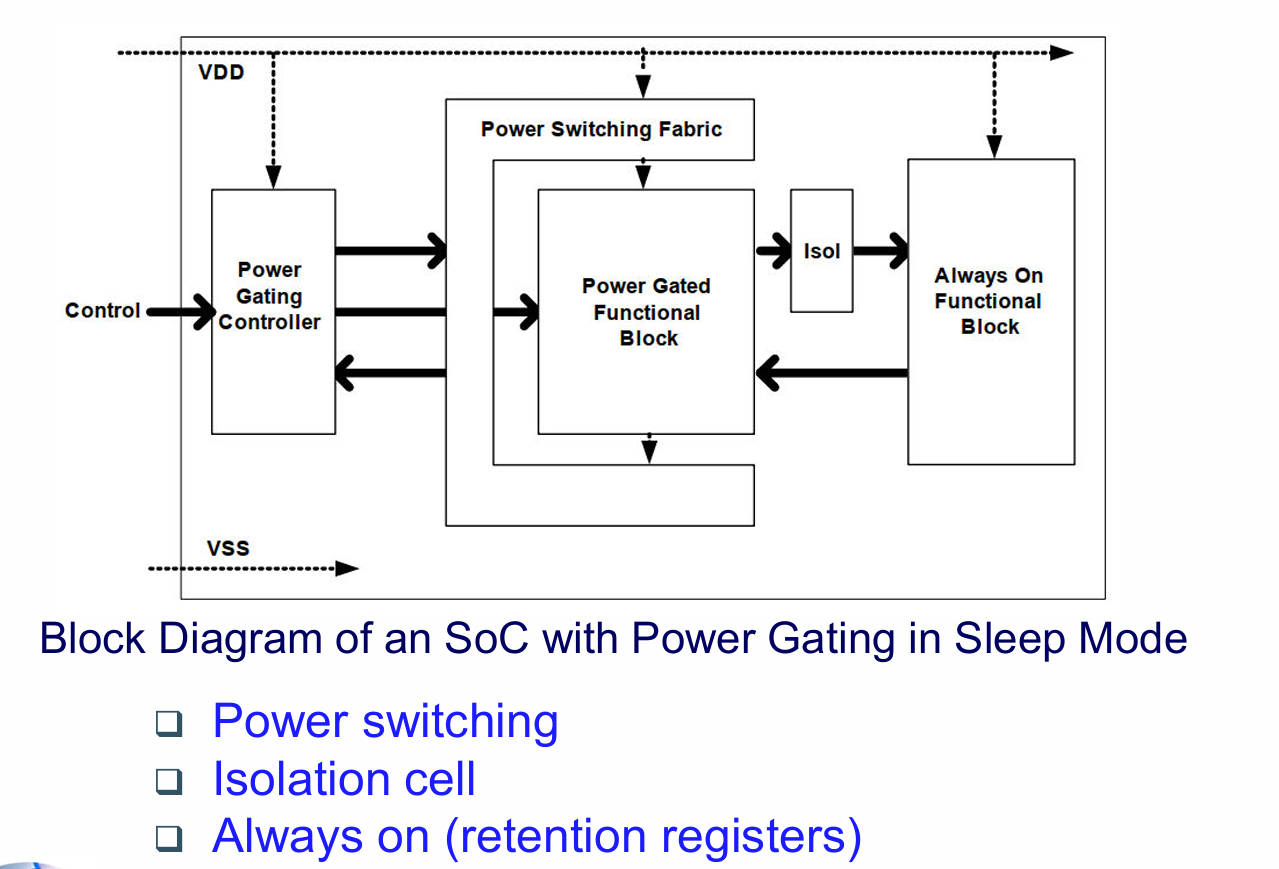
alt text

体偏置技术 (Body Biasing)
通过改变晶体管的衬底（体）电压来动态调节其阈值电压。

原理： 对于NMOS，增加体-源电压 V_bs（负向偏置）会提高 V_th，从而减小漏电流。对于PMOS，减少体-源电压 V_bs（正向偏置）会提高 |V_th|，减小漏电流。

类型：
反向体偏置 (Reverse Body Biasing, RBB)： 在工作时施加，可以降低 V_th，提高速度（用于性能提升）。
正向体偏置 (Forward Body Biasing, FBB)： 在待机或睡眠模式下施加，提高 V_th，显著降低漏电流。
实现： 需要特殊的制造工艺支持（如SOI - 绝缘体上硅，或体硅中的独立阱）。
优点： 可以动态调节，灵活性高。
缺点： 工艺复杂，增加了电源网络的复杂性（需要额外的偏置电压），可能影响可靠性。

PPA优化

EDA工具

常见电路

参考书籍：
《Digital Integrated Circuits— A Design Perspective》
《Computer arithmetic：algorithms and hardware designs》
《Verilog高级数字系统设计技术与实例分析》第6章

逻辑门

Memory

加法器

乘法器

参考：《Computer arithmetic：algorithms and hardware designs》Parhami, Behrooz， 第9章

移位乘法器

原理

首先考虑无符号的整数乘法，即：

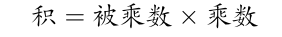
不妨考虑一个最简单的4位乘法的情况：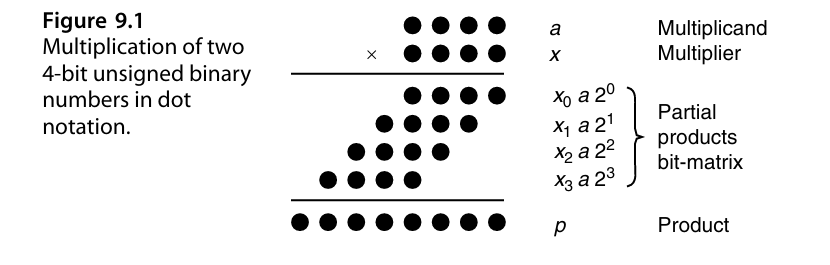

乘数表示为a，被乘数x的每一位为$x_0,x_1,x_2,x_3$。一个很自然的想法是分别取出被乘数x的每一位，与a进行乘法(与操作)，之后乘以2的幂。

左移还是右移：
上述算法的流程，可以通过左移或者右移实现。右移看上去似乎比较自然，每次右移都是取出了x的最低位，并且与a相乘相加。右移可以将上述式子从上到下进行累加，其迭代公式如下：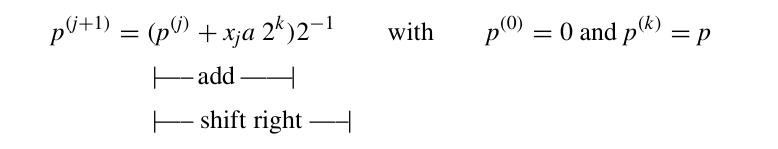

需要注意的是，这个公式每次将总体结果右移了移位，k次之后相当于总体右移了k位，为了抵消这种操作，需要提前将a左移k位。这很容易实现，只需要将a的值放在一个2k宽度的寄存器的前k位即可。在经过k次迭代后，我们有：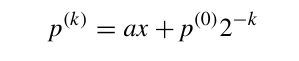

可以看到，如果将部分和$p_0$初始化为0，计算得到的是一个简单的乘法:
$$p=ax$$

如果将其初始化为$y2^k$,则可以计算$ax+y$,也就是乘加操作。这样的好处是不需要额外的硬件资源。右移的计算过程如下：

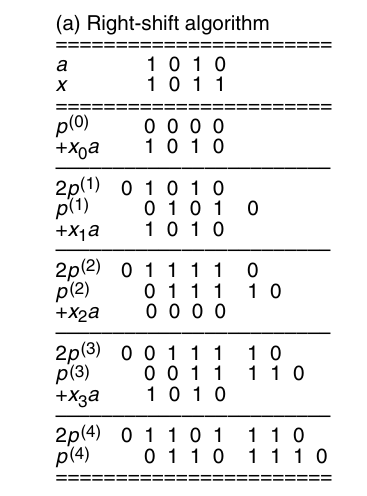
我们可以写出如下算法流程：

对应的电路如下：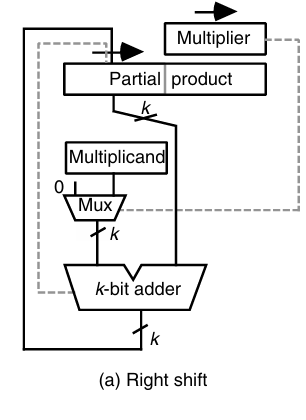

a的值一开始放在一个2k长度的部分积寄存器的左半边，每次取出其高k位，与经过x对应位选择的multiplicand相加，结果写回部分积寄存器的高k位。

右移乘法的好处是可以节省加法器的位宽，对应的加法器只需要k-bit,如果是左移计算，则需要2k位宽的加法器: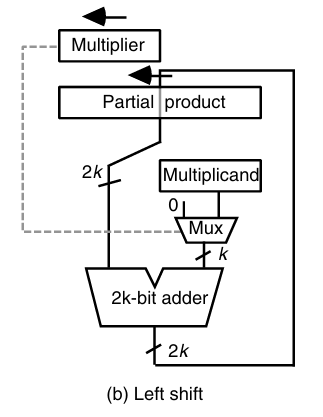

此外，我们可以将x放在部分积寄存器的后k位来进一步节约资源。考虑加法器的进位情况，最终的摆放如下：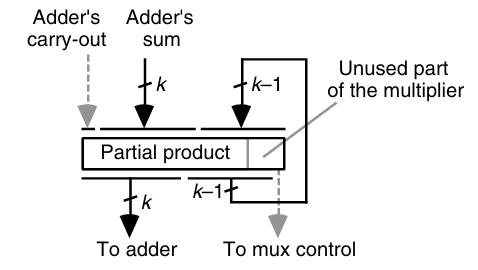

另外值得注意的一点是图中的mux，其实可以用一系列的与门来代替，与门的一端连接shift后x的一位。

如果是后续有符号的乘法，则使用真的mux,通过x来选择a,a的补码或者0。

有符号的移位乘法

对于有符号数，一个办法是在计算前，对负数计算其补码，得到对应的正数，正数相乘得到相应的绝对值，之后再根据
结果决定是否转化为负数。

但是这样的3个过程太慢了，可以考虑直接在每次迭代的时候进行计算，一个示例流程如下：

当乘数为负的时候，一开始正常的相乘相加。最后的符号位则需要计算减法(2’s completion)。对应的电路结构如下：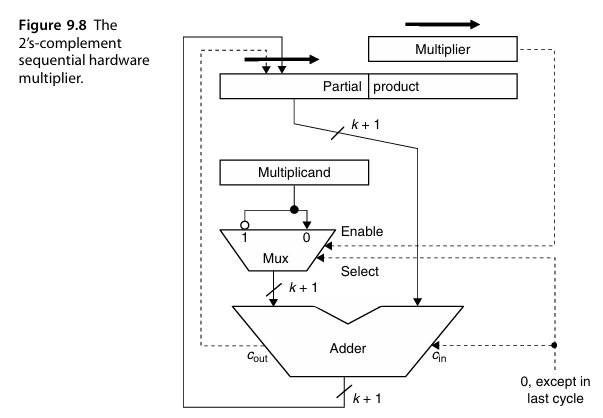

因为符号位的存在，这里使用一个k+1位的加法器。

BOOTH编码

此外还可以使用booth编码，将{0，1}集合表示的数映射到{-1,1}的集合上去。

另外，一个数x乘以一个常数a的问题，如果常数a已知，可以转化为一系列移位加法。

例如8’b11010001,可以将1分别左移7，6，4位后求和，然后再+1。

这是因为加法和移位运算是图灵完备的。但这种方法的问题在于，一个数的二进制表达中的1越多，所需要的加法次数就越多，相应的周期也就越长。

而结合booth编码，可以同时引入加法，减法和移位运算，例如，C=23，其二进制表示为
10111而：
$$
23=2^4−2^2+2^1+2^0 $$

这样可以有效减少指令数目

因此，在无法乘法和除法并不是计算机的基础指令，而是可以通过编译器将其修改为一系列移位和加减法来间接实现。在乘以一个常数时，如果乘法占用的周期数过高，也可以通过编译器优化为移位和乘法来解决。
有趣的是，给定一个整数常数 $C$，如果允许使用移位、加法和减法的组合，找到最优的（最少操作数的）表达形式确实是一个NP 完全问题。这个问题在计算机科学中被称为最小移位加法问题（Minimum Addition-Subtraction Chains Problem）。

高基乘法器

上面的移位乘法器存在一个问题，就是每次只能计算1位，运算周期过长，这在现代处理器中往往是不可接受的。

一个自然的相反是一次计算多位，也就是采用高基乘法器。

例如，一个k位的二进制数，也可以看成是k/2位基数(radix)为4的数（即k/2位4进制数），或k/4位，基数为8的数。

除法器

移位除法器

无符号除法

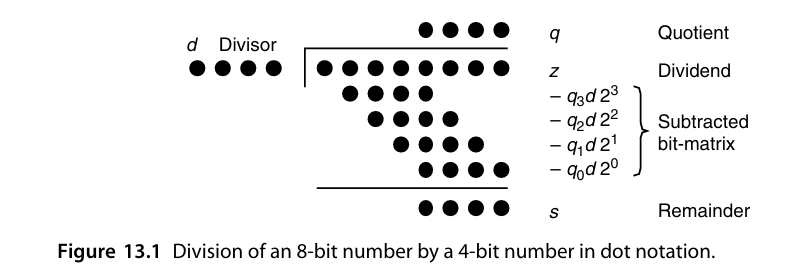
一个典型的二进制整数除法的流程如图，2kbit的被除数z除以除数d,商为q,余数为s。

由于结果q的每一位不是0就是1，其与d的乘积不是0就是d本身。所有问题转化为z对d或d的移位结果的一系列减法。

在一系列右移减法的过程中，除法的问题在于，一开始不知道商q的每一位是0还是1，需要一次额外的估计(比较)操作来得到商的一位，然后再执行减法。

此外除法与乘法的另一个不同在于，虽然2个k位数的乘积不会超过2k位，但是一个2k位的数除以k位的数，其结果可能超过K位(这很好理解，除数为1的极端情况下，结果不变还是2k位)。因此在计算之前，需要进行溢出检测：

如果要得到一个k位的商q，那么q一定小于$2^k$,而余数s一定小于d,估算z的最大值，有：
$$z < (2^k-1)d + d < 2^kd$$

也就是说d左移k位后一定大于被除数z,换言之，z的最高k位必须小于d,才能保证商的位数小于等于k。

图13.1可以用下面的迭代公式来表示：

除法是一个左移迭代算法，因为商q的每一位结果是从高到底获得的，q乘以2^d是为了这一点。在k次迭代后，有：

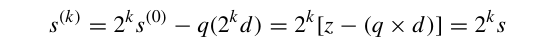
一个例子如下：

对应的算法为：

需要注意的是，当且仅当每次被除数的前k位大于除数时，才执行减法操作，否则应当保持被除数不变，下一次移位后再计算(对应该位的商为0时的情况)。

而被除数前k位大于除数，有以下2种可能：

  1. 加法器的进位 cout = 1;
  2. 余数寄存器的最高位为1(因为移位后可以获得$2^{k+1}$,而任何一个k bit的数小于$2^{k+1}$)

只有这种情况满足时，商的对应位才为1，同时执行减法。

一个verilog实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
module divider #(
    K = 32
) (
    input [2*K-1:0]  dividend,
    input [K-1:0]    divisor,

    output [K-1:0]  qoutient, 
    output [K-1:0]  remainder,

    input  valid_i,
    input  ready_i,
    output busy, // the divider is busy in computing
    output valid_o,
    output ready_o,
    input clk,
    input rst_n 
);
    localparam WIDTH = $clog2(K);
    reg [K-1:0] Rp; // rp is initialized to  high k bits of dicidend
    reg [K-1:0] Rq; // rq is initialized to  low  k bits of dicidend
    reg [WIDTH:0] Rc; // shift counter, initialized to K
   
    reg valid;
    // combinational logic

    wire [K-1:0] neg_divisor  = ~divisor;
    wire cout;
    wire [K-1:0] adder_result;
    wire zero_flag;
    wire overflow_flag;
    wire load_en = Rp[K-1] | cout;
    
    wire [K-1:0] Rp_shift = {Rp[K-2:0],Rq[K-1]};
    wire [K-1:0] Rp_next = load_en ? adder_result : Rp_shift;
    wire [K-1:0] Rq_next = {Rq[K-2:0],load_en};

     adder #(.N(K)) u_adder(
        .A             (Rp_shift             ),
        .B             (neg_divisor             ),
        .carry_in      (1'b1      ),
        .result        (adder_result        ),
        .zero_flag     (zero_flag     ),
        .overflow_flag (overflow_flag ),
        .carry_out     (cout     )
    );

    always @(posedge clk or negedge rst_n) begin
        if(!rst_n)begin
            Rc <= {(WIDTH+1){1'b0}};
        end
        else if (~busy & valid_i)begin
            Rc <= K;
        end
        else begin
            Rc <= Rc - 1'b1;
        end
    end

    always @(posedge clk or negedge rst_n) begin
        if(!rst_n)begin
            Rp <= {K{1'b0}};
        end
        else if (~busy & valid_i)begin
            Rp <= dividend[2*K-1:K];
        end
        else begin
            Rp <= Rp_next;
        end
    end

    always @(posedge clk or negedge rst_n) begin
        if(!rst_n)begin
            Rq <= {K{1'b0}};
        end
        else if (~busy & valid_i)begin
            Rq <= dividend[K-1:0];
        end
        else begin
            Rq <= Rq_next;
        end
    end

    always @(posedge clk or negedge rst_n) begin
        if(!rst_n)begin
            valid <= 1'b0;
        end
        else if ( valid_i & (Rc == {{WIDTH{1'b0}}, 1'b1}))begin
            valid <= 1'b1;
        end
    end


    assign busy = (Rc != {(WIDTH+1){1'b0}});
    assign ready_o = ~busy & ready_i;
    assign valid_o = valid & ~busy;
    assign qoutient = Rq;
    assign remainder = Rp;
    
endmodule

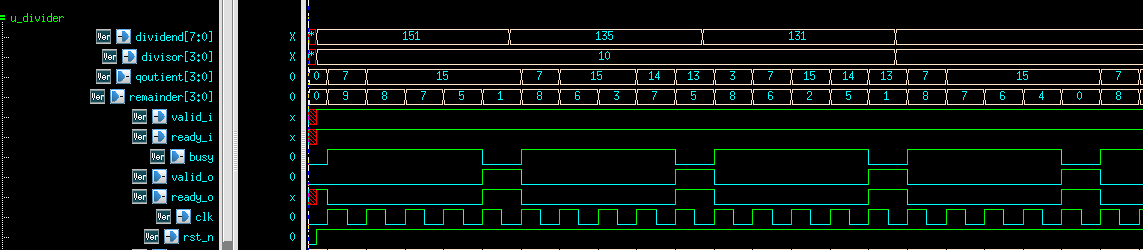
alt text

事实上，这种实现叫做restoring的算法，每次需要判断加法器的结果，才能决定寄存器需要更新的值。

如果进行时序分析，则每个时钟周期需要做到以下事情：

如果想要优化这个时序，可以使用non-restoring的算法。

在 non-restoring算法种，每个周期都减去一个被除数，而如果当时的余数小于被除数而错误的剪掉了一个被除数，则可以在下一个周期加回来。
这是因为下一个周期会进行shift left的操作，相当于已经提前减去了2个被除数，因此只需要再加上一个被除数，仍然能达到减去一个被除数的效果。

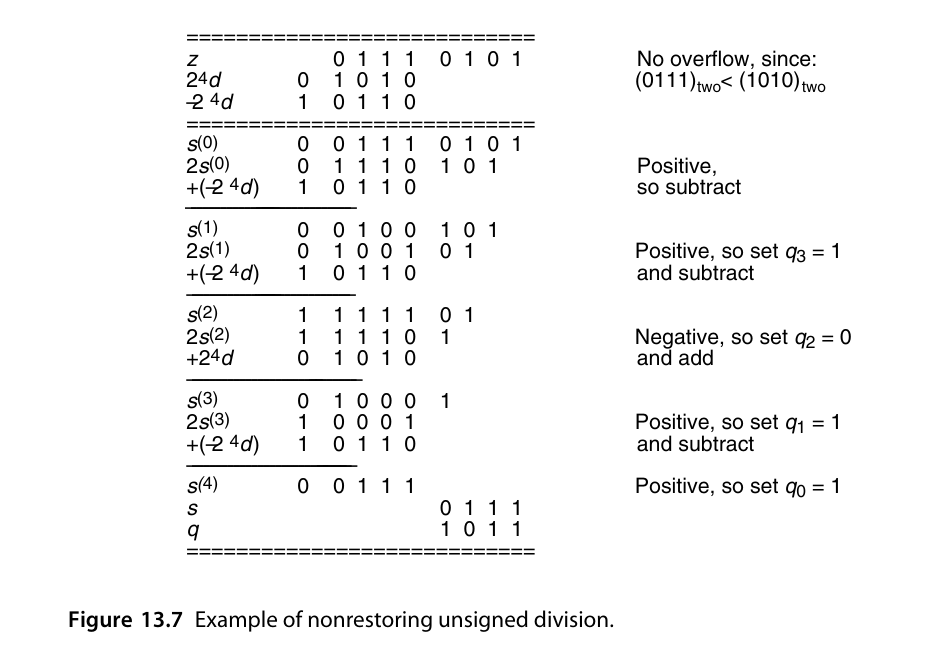
有符号除法

在上述的restoring 算法中，每个周期总是减去一个被除数或是不减，也就是说被除数的系数为{0,-1},而在non-restoring的算法中，没周期总是
减去或加上一个被除数，也即其系数为{-1,1}。而在除法结束时，余数的符合总是与被除数相同(这是有符号除法的定义决定的)。

因此，可以考虑直接处理有符号除法：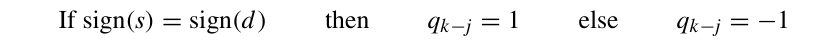

若当前的余数与被除数的符合相同，则q对应的位为1，否则为-1。

而在计算结束后，还需进行如下步骤：

即

  1. 先将商的表示由{-1,1}的二进制空间映射回标准的{0,1}空间。
  2. 如果余数的符合与商的不一致，说明多减去/加上了一个被除数。需要对结果进行矫正。

对于1，做法应该是：

即将所以的对应位置的-1变为0，然后将最高位取反，整体左移一位后最低位补1。这种转化很简单，可以通过硬件，在计算出商的同时完成。

在初始化时先设置商的符号位，然后根据之后每次是加法还是减法操作来生成对应位的0,1,最后在商的末尾补1.

对于2：

矫正时需要将商加上或减去1，同时将余数减去或加上被除数。由于1的变化算法使得商的最后一位为1，导致商总是奇数，因此当商为偶数时，矫正不可避免。

该算法的一个示例过程如下：

对应的电路为：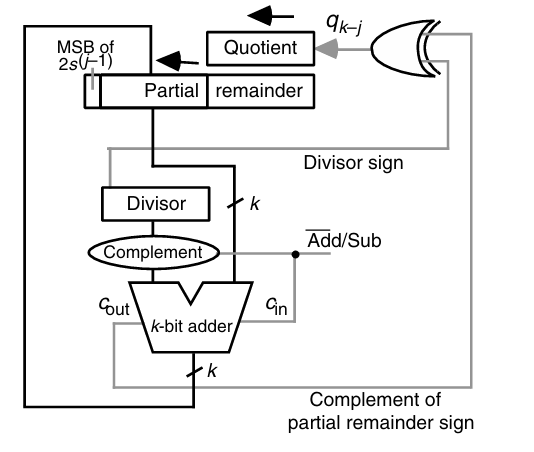

根据上述思路实现的移位除法器代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
//=====================================================================
//
// Designer   : wenkai_sjtu@163.com
//
// Description:
//  an signed left shift divider, using nonerestoring algrithm
//  no overflow and zero  divisor check
// Revision History: 
// ====================================================================

module signed_divider #(
    K = 32
) (
    input [2*K-2:0]  dividend,
    input [K-1:0]    divisor,

    output [K-1:0]  qoutient, 
    output [K-1:0]  remainder,

    input  valid_i,
    input  ready_i,
    output busy, // the divider is busy in computing
    output valid_o,
    output ready_o,
    input clk,
    input rst_n 
);

    //   use state machine 
    localparam IDEL = 2'b00, SHIFT=2'b01, CORRECT = 2'b10, OUTPUT = 2'b11;

    localparam WIDTH = $clog2(K) + 1; // expand 1 bit to avoid overflow 

    reg [K-1:0] Rp; // rp is initialized to  high k bits of dicidend
    reg [K-1:0] Rq; // rq is initialized to  low  k bits of dicidend
    reg [WIDTH-1:0] Rc; // shift counter, initialized to K
    reg [1:0]   state; // the state of divider
    reg [1:0]  state_next;

    wire sign_dividend = dividend[2*K-2]; // sign bit of dividend
    wire sign_divisor = divisor[K-1]; // sign bit of divisor 
    wire sign_remainder = Rp[K-1];//  sign bit of remainder

    wire [K-1:0] divisor_neg = ~divisor;  // 1's complement of divisor
    wire shift_sub = ~(sign_remainder ^ sign_divisor); // sign of remainder equal to sign of divisor, sub ,otherwise add
    wire need_correct;
    wire correct_sub;
    reg  sub;   // substract flag of adder

    wire cout;
    wire [K-1:0] adder_result;
    wire zero_flag;
    wire overflow_flag;


    wire [K-1:0] Rp_shift = {Rp[K-2:0],Rq[K-1]};
    wire [K-1:0] Rq_shift =  {Rq[K-2:0],shift_sub};
    wire [K-1:0] Rq_con = {~Rq[K-2],Rq[K-3:0],1'b1};

    reg [K-1:0] addend1;  // operand 1 of adder, net
    reg [K-1:0] addend2;  // operand 2 of adder, net
    reg [WIDTH-1:0] Rc_next;
    reg [K-1:0] Rq_next ;
    reg [K-1:0] Rp_next ;



    adder #(.N(K)) u_adder(
        .A             (addend1             ),
        .B             (addend2             ),
        .carry_in      (sub      ),
        .result        (adder_result        ),
        .zero_flag     (zero_flag     ),
        .overflow_flag (overflow_flag ),
        .carry_out     (cout     )
    );

    // when shift finish, the result needs correct if sign of remainder is different to sign of dividend
    assign   need_correct = (Rc == {WIDTH{1'b0}})  & (sign_remainder ^ sign_dividend);

    assign   correct_sub =  need_correct & (  
            (sign_remainder  & sign_divisor) // remainder < 0, divisor < 0 but dividend > 0
        |   (~sign_remainder & ~sign_divisor)); // remainder > 0, divisor > 0 but dividend < 0
        // in this 2 case we need to substract another divisor to correct the result otherwise we need to add

    always @(*) begin
        // default value
        Rp_next = dividend[2*K-2:K-1];
        Rq_next = {dividend[K-2:0],1'b0};
        Rc_next = K-2;
        sub = shift_sub;
        addend1 =  Rp_shift;
        addend2 =  shift_sub ? divisor_neg : divisor;
        case (state)
        IDEL : begin
            if(valid_i)begin
                state_next = SHIFT;
            end
            else begin
                state_next = IDEL;
                Rp_next = Rp;
                Rq_next = Rq;
                Rc_next = Rc;
            end
        end 
        SHIFT:begin
            Rp_next =  adder_result;
            Rq_next =  Rq_shift;            
            sub = shift_sub;
            addend1 =  Rp_shift;
            addend2 =  shift_sub ? divisor_neg : divisor;
            if(Rc != {WIDTH{1'b0}})begin
                state_next = SHIFT;     
                Rc_next =  Rc-1'b1;     
            end
            else begin
                state_next = CORRECT;
                Rc_next = Rc;  // keep rc=0
            end
        end
        CORRECT:begin
            state_next = OUTPUT;
            Rp_next = need_correct ? adder_result : Rp;
            Rq_next = need_correct ? (correct_sub ? Rq_con + 1'b1 : Rq_con - 1'b1) : Rq_con;
            Rc_next = Rc;
            addend1 = Rp;
            addend2 = correct_sub ? divisor_neg : divisor;
            sub = correct_sub;
        end
        OUTPUT:begin
            if(ready_i & ~valid_i)begin // wait next data 
                state_next = IDEL;
            end
            else if (ready_i & valid_i)begin // begin next computation
                state_next = SHIFT;
            end
            else begin  // wait result to be stored
                state_next = OUTPUT;
                Rp_next = Rp;
                Rq_next = Rq;
                Rc_next = Rc;
            end
        end
        endcase
    end

    always @(posedge clk or negedge rst_n) begin
        if(!rst_n)begin
            state <= IDEL;
            Rp    <= {K{1'b0}};
            Rq    <= {K{1'b0}};
            Rc    <= {WIDTH{1'b0}};
        end
        else begin
            state <= state_next;
            Rp    <= Rp_next;
            Rq    <= Rq_next;
            Rc    <= Rc_next;
        end
    end

    assign busy = ((state == SHIFT) | (state == CORRECT));
    assign valid_o = (state== OUTPUT);
    assign ready_o =  ~busy & ready_i;
    assign qoutient = Rq;
    assign remainder = Rp;

endmodule

上述实现采用状态机进行控制，在移位完成后的一个周期内进行结果矫正，之后输出。使用时需要自行保证除数非0以及无溢出。
(即前面讨论的,被除数的高K位必须小于除数，有一个简单的做法是对被除数进行符号扩展，比如32位的有符号除法，先将被除数扩展为63位再进行计算，可以避免溢出)。

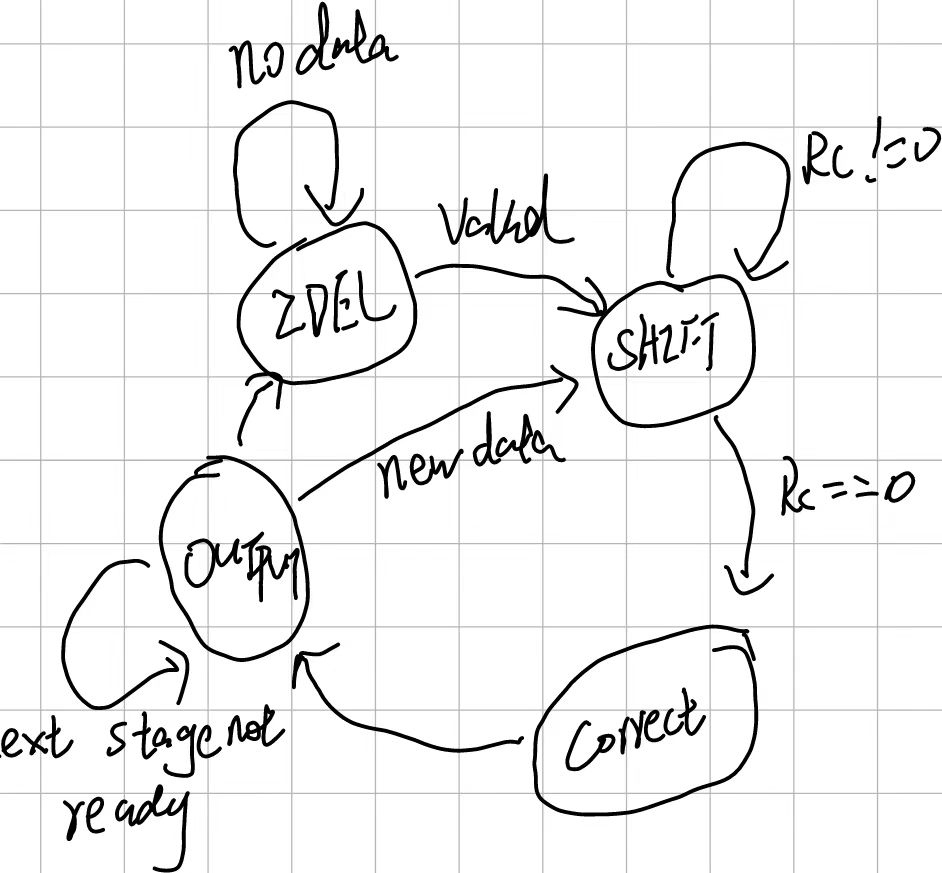{width=300 height=200 align=center}

格雷码

LFSR

FSM

参考：《Finite State Machine (FSM) Design & Synthesis using SystemVerilog》

纠错与校验

FIFO

异步FIFO参考：《Simulation and Synthesis Techniques for Asynchronous FIFO Design with Asynchronous Pointer Comparisons》

体系结构

参考书籍：
《Computer Architecture: A quantative approach, 6th edition》
《计算机体系结构》胡伟武
《通用图形处理器设计》景乃锋
上海交通大学《高等计算机体系结构》课程
《Efficient Processing of Deep Neural Networks》
《A Primer on Memory Consistency and Cache Coherence》

ILP

流水线

Memory Hierarchy

DLP

GPGPU基础

NPU概述

SMP & Memory coherency

RISC-V

SoC

常见IP及其功能

AMBA总线

AXI

AXI4和 AXI4 Lite的区别？

是否支持burst, 缓存属性操作，aomic,和exclusive

想要实现burst传输，master侧需要哪些组件支持？

  1. 状态机和计数器，控制axlast信号的生成
  2. 地址生成模块，通过判断burst的类型是递增，回绕，固定，来生成每个transfer的地址
  3. 配置寄存器

如果想要实现outstanding比较大的master，如何实现？
reorder buffer管理不同id。

为什么写操作比读多了一个独立的bresp 通道？

主要是数据流决定的，不如说读通道少了一个单独的read response，读响应和读数据被合并了。

由于写数据的数据流是单项的只从master流向slave,因此需要read response来通知master写操作的完成情况。

为什么要分离写数据和写地址？

提高吞吐量。解耦后对DMA传输友好。

AXI4和AXI3的区别？

删除了WID,不支持写交织。因为写交织容易造成死锁。

注意：保留了AWID信号，因此是支持写response乱序返回的。而由于没有wid的存在，写通道上的数据必须和写数据对应。
由AWID来区分每笔事务，由wlast来确定某笔传输是否结束。

AXI中各个Channel信号之间的依赖关系是什么？

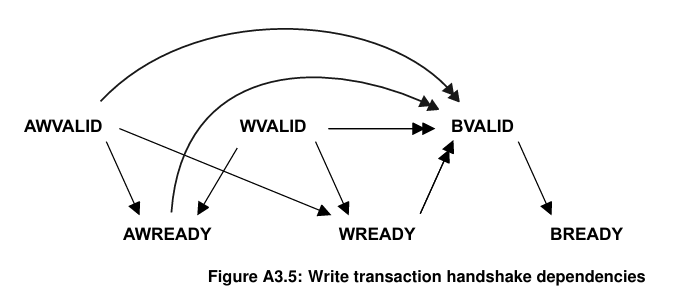
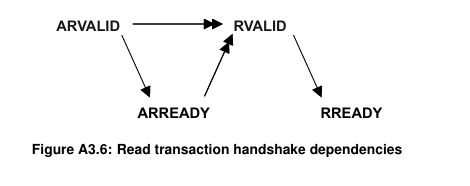
  • 单箭头指向可以在箭头前的信号之前或之后断言(拉高)的信号
  • 双箭头指向必须在箭头前的信号断言(拉高)之后才可以断言的信号。

简单来说，就是resonse必须等request完成后再返回。

如何实现interleaving

首先AXI4不支持写交织，读交织需要用到arid和rid。

例如，多笔burst传输的读返回可以交错进行。也就是说是transfer粒度的乱序。从效果上看，读响应的每笔transfer的id是交错进行的。

是否支持读交织主要是slave方面的设计。slave要维护一个table,存储所有未完成的arid，然后根据自身状态决定对每个未完成transaction的处理顺序。

如何实现outstanding和out of order?

out of order主要是针对slave的响应顺序，可以与接到的request顺序不同。
这需要master侧支持outstanding，即支持连续传输多个未完成的事务，并为每个事务生成一个不同的id进行维护。这需要master侧维护一个table, 来进行id分配和回收。

什么是burst传输，burst有哪些类型？

读burst:一笔读request对应多个读response,即多transfer的transaction
写burst:一笔写地址对应多笔写数据。

burst类型：

  • 固定：FIXED,主要用于写fifo
  • 递增：INCR,地址每次加SIZE，用于访问连续的内存
  • 回绕: WRAP,地址先每次加SIZE进行递增，超过回绕边界后回绕到起始地址附近。用于cache操作

warp如何计算回绕地址的上下界？

  1. 确定传输的total byte:
    例如axlength=4, axsize=8
    total byte = (4+1)*8=40 bytes

  2. 确定回绕边界
    回绕边界大小是大于或等于 Total_Bytes 的最小 2 的幂次方。
    大于等于40的最小2的幂次是64，故回绕边界warp_bound为64

  3. 计算回绕基址
    若axaddr=0x84
    warp_base= addr & ~(warp_bound -1) 清楚地位地址，进行对齐
    = 0x84 & ~0x3f
    = 0x80
    地址范围为(warp_base,warp_base + warp_bound -1) = (0x80, 0xbf)

    连续5笔传输的地址依次为： 0x84,0x8c,0x94,0x9c,0xa4

AXI传输中的内存类型有哪些？

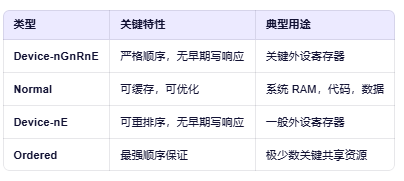
什么是exclusive和atomic?如何实现？

死锁

描述一种AXI协议的死锁场景？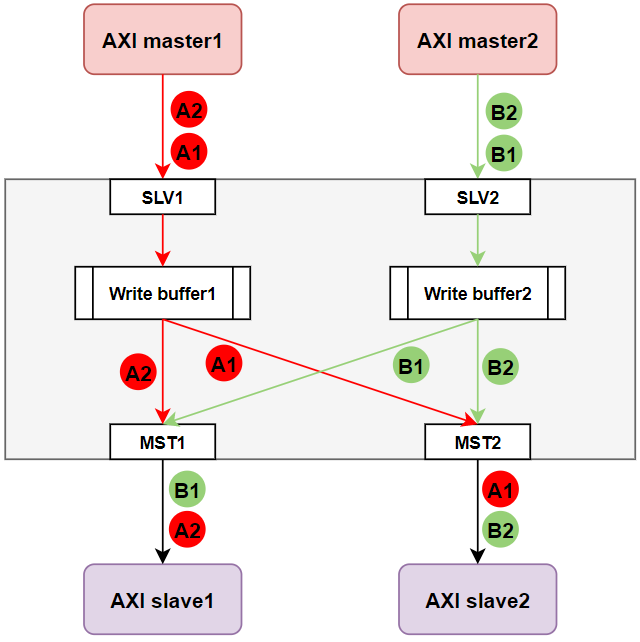

如图所示的一个2 Master 2 Slave总线，通过NoC进行连接。NoC上会出现乱序。假设：

  1. Write Buffer长度为8。
  2. Master1 分别发送2笔burst写，其中A1 写Slave2, A2写Slave 1
  3. Master2发送了2笔burst写，其中B1写Slave1,B2写Slave2
  4. 所有写的burst长度为9，且NoC的路由导致salve收到的AW的顺序为A2，B1，slave2收到的AW顺序为B2,A1

下面是分析过程：

  • slave1先收到了Aw2，由于AXI协议中要求写数据和写请求(写地址)的顺序一致，因此它必须先处理所有A2的写数据再处理B1的写数据。
  • 同理，slave先收到了BW2，它必须先处理B2的写数据再处理B1的写数据。
  • 现在Master端开始发送A1和A2，B1和B2,假设它们是依次发送的
  • write buffer 1中写满了A1, write buffer2中写满了B1
  • slave1在等待A2，但A2只有在buffer1中的A1被处理后才能发出
  • buffer2中的A1在需要等slave2处理完B2才能被处理
  • slave2在等待B2被全部发送，但B2需要等待Buffer2中的B1被处理后才能发出
  • buffer2中的B1需要等待slave1处理完A2后才能被处理

由此形成了如下图所示的循环依赖，也就形成了死锁。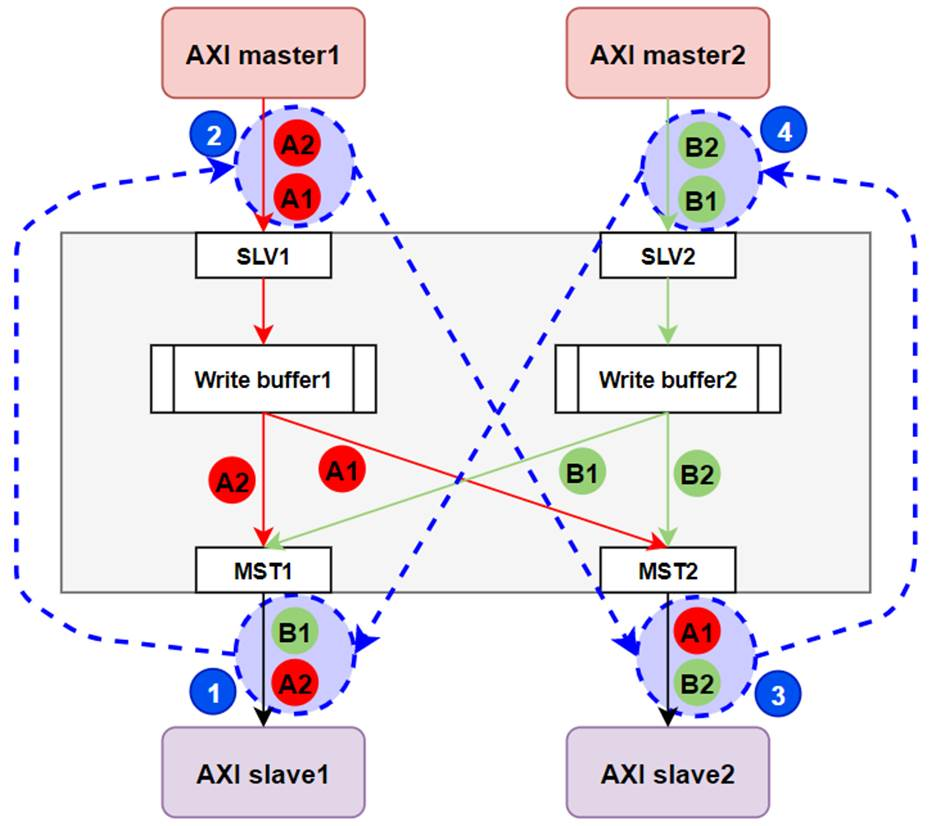

核心是形成了某种循环依赖。

如何打破上述死锁？

  • 总线层面进行检查，接到A2时，如果发现有未完成的请求A1，就暂时不把A2发给slave1，从而避免死锁。
  • 增大buffer容量
  • 限制master的outstanding

AHB

APB

CHI

NoC

参考：
《Principles and practices of interconnection networks》
《On-Chip-Networks-2nd-Edition》

代码、验证与工程

参考书籍：
《IEEE Standard for Verilog Hardware Description》
《System Verilog验证 测试平台编写指南》
《UVM实战》
《uvm-cookbook-complete-verification-academy_compress》
《IEEE Standard for Universal Verification Methodology Language Reference Manual 》
《SystemVerilog_3.1a》

Verilog 技巧

验证基础

参考：
《Cracking Digital VLSI Verification Interview》

  1. directed testing 和 random verification的区别是什么？
    直接测试是用一系列手写的测试来检验dut的功能。随机测试由生成器generator针对spec随机生成。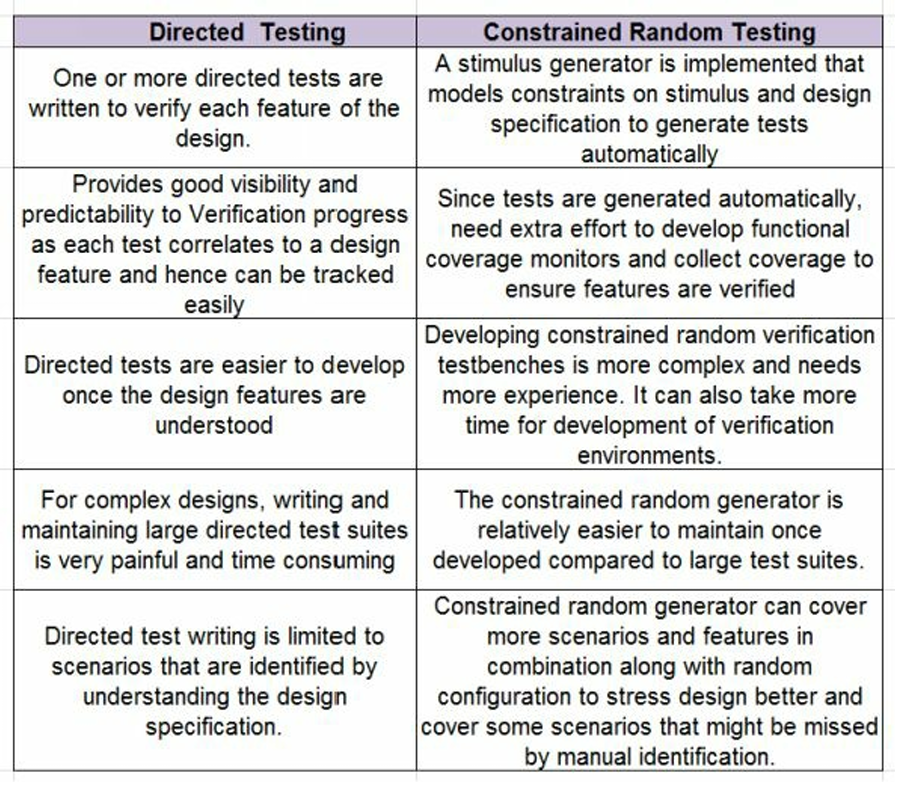


    验证中需要组合使用2种策略，以保证覆盖足够多的coner case,使设计被充分验证。

  2. 什么是self-checking tests?
    能够通过某种方法检查测试结果的测试。例如通过对某些内存操作结果进行计算或收集DUT的信息(如状态寄存器等)，从而预测测试的结果。

  3. 什么是覆盖率驱动的验证(coverage driven verification)？
    在覆盖率驱动的验证方法学中，验证计划可以通过将一系列feature或场景(scenario)映射到对应的覆盖率监视器(coverage monitor)中来实现。coverage monitor可以在仿真中收集对应的覆盖信息。

    • coverage monitor可以是基于sample的covergroup和基于特性(property)的coverage的组合
    • 在基于覆盖率的验证中，测试通常使用受约束的随机激励生成器( constrained random stimulus generator)生成，测试的正确性由功能检查器（ functional checkers）确保，并针对所有覆盖率监视器进行覆盖率收集。
    • 通常，随机生成器的多个测试或多个种子在设计上回归，并从每个测试中收集的单个覆盖率合并以获得累积覆盖率。有时，使用约束随机刺激可能无法轻松覆盖设计中的极端情况，使用定向检验可能会更好。
    • 覆盖率信息还为生成器中的测试和约束的质量提供反馈，并有助于微调约束以实现高效的随机激励生成。
    • 因为在这种方法中，覆盖率定义是跟踪验证执行进度和完成的关键步骤，所以确保根据验证计划和设计规范审查覆盖率定义和实现的完整性和正确性是很重要的。

  4. 功能验证中的test grading是什么？
    设计的功能验证是通过创建定向测试以及添加了不同激励控制的约束随机激励生成器来完成的。通过验证项目，开发了一组测试，该测试套件用于验证设计正确性、查找设计中的错误以及收集覆盖率等。
    测试评分(test grading)是一个过程，在这个过程中，根据不同的标准（如功能覆盖率命中、发现的错误、模拟运行时间、易于维护等）对单个测试进行质量评级。
    此过程有助于从测试套件(test suite)中识别出有效的测试，从而为设计验证开发最有效的测试套件。

  5. 什么是基于断言的验证方法学(Assertion based Verification methodology,ABV)？
    基于断言的验证 （ABV） 是一种使用断言来捕获特定设计意图的方法。然后，这些断言用于仿真(simulation)、形式验证和/或模拟(emulation)，以验证设计实现是否正确。ABV 方法可以补充其他函数验证方法，通过利用断言的优势实现高效验证。断言的一些好处如下:

    • 断言从源头检测设计错误，从而有助于提高可观察性并缩短调试时间。
    • 相同的断言可用于仿真和形式化分析，甚至可以用于模拟(emulation)。
    • 断言库中提供了许多用于通用设计的断言，并且可以轻松移植到任何验证环境中。
    • 作为属性编写的 SystemVerilog 断言也可用于覆盖率（使用 cover 属性），因此有助于基于覆盖率的验证方法。

  6. event driven 的仿真器和cycle based的仿真器的区别？
    事件驱动的仿真通过获取每个事件及传输的变化直到达到稳态条件来评估每个事件的设计。事件被定义为设计元素(design element)的任何输入的变化。由于 inputs 的到达时间和来自下游 design elements 的信号反馈不同，因此 design element 可以在一个周期中被多次评估。
    例如，考虑2级寄存器之间的组合逻辑，组合逻辑路径可以有多个 gate 和 feedback path。在一个时钟周期内，当第一个 flip-flop 的 output 发生变化时，它被施加在 logic path 的 input 上，并且 组合逻辑中不同阶段的 input 的任何变化都将触发该特定 design 的评估。这可能需要多次评估才能使值稳定下来，并且在该 clock cycle中不再更改。大多数行业广泛使用的仿真器都是事件驱动的，例如：Mentor 的 Questa、Synopsys 的 VCS 或 Cadence 的 Incisive Simulator。这是因为事件驱动型仿真器提供了准确的仿真环境。

    Cycle-Based Simulators 在一个 clock cycles 中没有时间的概念。它们在一次测试中评估 state 元素和/或 ports 之间的逻辑。这有助于显著提高仿真速度，因为每个 logic element 每个周期只评估一次。缺点是它无法真正检测到 signals 中的任何 glitch，并且它仅在完全同步的 logic designs 上才能正常工作。由于在 simulation期间没有考虑 设计时序，因此需要使用一些静态时序分析工具单独进行时序验证。基于循环的模拟器在一般设计中不是很受欢迎，但在一些开发大型设计（如微处理器）的公司中是定制和使用。

  7. 什么是transaction的概念？transaction based verication有什么优势？
    transaction是一组更低级别信号的高层级抽象。虽然 designs 在 signal 级信息上运行，但 testbench 需要让 driver 和 monitor 在信号级与 design 连接，而 testbench 的所有其他方面都可以抽象为事务级。基于事务的验证是一种以分层方式构建测试平台的方法，其中只有较低层的组件在信号级别运行，所有其他组件都基于事务运行和通信，如下所示。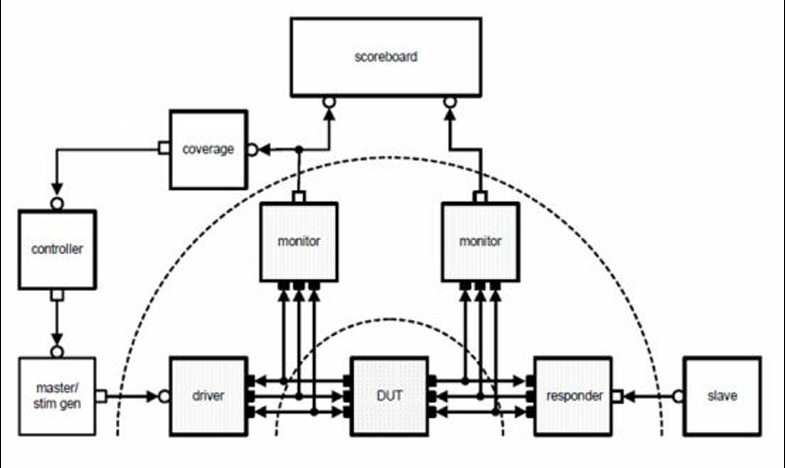

  • 基于事务的验证的主要优点是可以在项目内或不同项目的不同验证环境中重用使用事务接口开发的组件。例如：参考上图，只有 driver、monitor 和 responder 需要有一个信号级接口。一旦这些组件将信号级信息分组到事务中，其他组件（如激励生成器(stimulus generators)、从机模型(slave model)和记分板(score board)）都可以对事务进行操作。
  • 由于事务组件需要由模拟器在事务边界上进行评估，而不是在每个信号变化时进行评估，因此仿真可以更快一些。
  • 如果 design 在接口时序方面发生变化，则只有 driver 和 monitor 组件需要更改，而其他组件将不受影响。

SV

UVM

UVM 是一种标准的验证方法，在验证行业中越来越受欢迎和更广泛地采用。该方法由 Accellera 创建，目前是 IEEE 标准化工作组 1800.2 的成员。UVM 由构建测试平台和测试用例的定义方法组成，还附带一个类库，有助于轻松构建高效的约束随机测试平台。

  1. UVM的优点是什么？
    UVM 包含构建测试平台和测试用例的定义方法，还附带一个类库，有助于轻松构建高效的约束随机测试平台。该方法的一些优点和重点包括：

    • 模块化和可重用性 - 该方法设计为模块化组件（驱动程序、定序器、代理、环境等），这使得能够在单元级到多单元或芯片级验证以及跨项目重用组件。
    • 将测试与测试平台分开 - stimulus/sequencers方面的测试与实际的测试平台层次结构分开，因此激励可以在不同的单元或跨项目之间重复使用。
    • 独立于模拟器 - 所有模拟器都支持基类库和方法，因此不依赖于任何特定的模拟器。
    • 序列方法（Sequence methodology）可以很好地控制刺激的产生。有几种方法可以开发序列：随机化、分层序列、虚拟序列(randomization, layered sequences, virtual sequences)等。这提供了良好的控制和丰富的刺激生成能力。
    • 配置机制简化了具有深层次结构的对象的配置。配置机制有助于根据使用它的验证环境轻松配置不同的 Testbench 组件，而无需担心任何组件在 Testbench 层次结构中的深度。
    • 工厂机制可轻松简化组件的修改。使用 factory 创建每个组件后，可以在不同的测试或环境中覆盖这些组件，而无需更改底层代码库。

  2. UVM的缺点？

    • 学习曲线比较陡峭，对新手并不友好。
    • 仍在发展当中，可能导致仿真变慢或存在某些潜在bug

  3. 什么是TLM，Transaction Level Modeling?
    事务级建模 （TLM） 是一种在更高抽象级别对任何系统或设计进行建模的方法。在 TLM 中，不同模块之间的通信是使用 Transactions 建模的，从而抽象出所有低级实现细节。这是验证方法中使用的关键概念之一，用于提高模块化和重用方面的生产力。尽管 DUT 的实际接口由信号级活动表示，但大多数验证任务（如生成激励、功能检查、收集覆盖率数据等）都可以通过独立于实际信号级细节，更好地在事务级别完成。这有助于在项目内部和项目之间重用和更好地维护这些组件。

  4. 什么是TLM ports和exports?

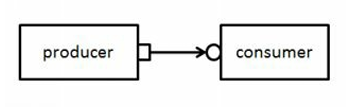
    在TLM中，不同的组件通过transaction进行通信。一个tlm port定义了一组用于特定连接的方法(API)，而这些方法的具体实现被成为tlm exports。tlm port和export之间的连接在2个组件之间建立了通信机制。

    例如这里有个producer（生产者）如何使用tlm port与消费者(consumer)进行通信的例子。 producer产生一个transaction并将其”put”到tlm port中，而 “put” 方法的实现，也称为 TLM export，将在consumer读取 producer 创建的transaction，从而建立通信渠道。

  5. 什么是UVM中的factory机制?
    UVM中的factory是一个特殊的look up table,所有的UVM组件和transaction需要在其中注册。UVM中通过create()方法进行组件和事务的注册。使用 factory 创建对象还有助于将一种类型的对象替换为派生类型的对象，而无需更改 TestBench 的结构或编辑 Testbench 代码。

面试常见问题

1.sv中function和task的区别？

  1. 延时：function不能用延时操作，被看作瞬时完成，tash中可以设置delay
  2. 返回值：function需要有返回值，task无返回值，但可以用input和output传递结果
  3. 调用：function只能调用其他function,task可以调用function和其他task

2. fork join,join_any,join_none的区别

  1. fork join创建的子进程会阻塞父进程，只有当fork的所有进程执行完毕后，才继续执行join后的代码
  2. join any的话，只要有一个子进程/线程执行结束，就会继续执行之后的代码
  3. join none并不会阻塞父进程，创建的进程只会被调度，在触发对应的条件后执行。

3. SV和UVM中进程间通信的方法
sv: event,mailbox,semaphore信号量
uvm: uvm_event，uvm_barrier，TLM，callback

4.UVM那些组件继承自object，哪些继承自component
uvm_object 是所有UVM对象的基类，提供了诸如复制、比较和打印对象等通用功能。典型的如uvm_sequence_item，uvm_analysis_port。
而uvm_component 是所有主要验证组件的基类，这些组件具有层次结构，并且遵循标准的阶段方法（如build_phase、run_phase等），用于控制组件的执行顺序。如driver,monitor,agent,env,scoreboard等。
5. monitor和driver的区别
uvm_monitor（监视器）：
功能：监视器的主要功能是被动地监视DUT（被测设计）的接口信号，并将这些信号转换为事务级对象（transaction objects）。它不主动驱动信号，而是观察信号的变化。
作用：监视器通常用于收集DUT的输出数据，并将其传递给其他组件（如uvm_scoreboard或uvm_subscriber）进行进一步的处理和验证。
典型用途：用于验证DUT的行为是否符合预期，例如检查协议的正确性、数据的完整性等。
uvm_driver（驱动器）：
功能：驱动器的主要功能是主动地将事务级对象转换为信号级操作，并驱动这些信号到DUT的输入端口。它负责生成和控制DUT的输入信号。
作用：驱动器通常用于将测试激励（test stimulus）传递给DUT，从而触发DUT的行为。
典型用途：用于生成各种测试场景，验证DUT在不同输入条件下的行为。

建模与SystemC

脚本语言

Make基础

手撕代码

时钟分频

占空比为1任意倍的奇数分频

通过一个计数器来对时钟周期计数，2个信号分别由原始时钟的上升沿和下降沿触发，通过或操作来满足占空比要求。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
`timescale 1ns/1ns

module clk_divider
    #(parameter dividor = 5)
( 	input clk_in,
	input rst_n,
	output clk_out
);
    localparam COUNTER_WIDTH = $clog2(dividor) + 1 ;
	reg [COUNTER_WIDTH-1 : 0] clk_counter1;
	reg clk_out_r1;
	reg clk_out_r2;

	always @(posedge clk_in or negedge rst_n)begin
		if(~rst_n)begin
			clk_counter1 <= {COUNTER_WIDTH{1'b0}};
		end
		else if(clk_counter1== dividor-1 )begin
			clk_counter1 <= {COUNTER_WIDTH{1'b0}};
		end
		else begin
			clk_counter1 <= clk_counter1 + 1'b1; 
		end
	end

	always @(posedge clk_in or negedge rst_n)begin
		if(~rst_n)begin
			clk_out_r1 <= 1'b0;
		end
		else if (clk_counter1 == dividor >> 1)begin
			clk_out_r1 <= ~clk_out_r1;
		end
		else if (clk_counter1 == dividor-1)begin
			clk_out_r1 <= ~clk_out_r1;
		end
	end

	always @(negedge clk_in or negedge rst_n)begin
		if(~rst_n)begin
			clk_out_r2 <= 1'b0;
		end
		else if (clk_counter1 == dividor >> 1)begin
			clk_out_r2 <= ~clk_out_r2;
		end
		else if (clk_counter1 == dividor-1)begin
			clk_out_r2 <= ~clk_out_r2;
		end
	end


	assign clk_out = clk_out_r1 | clk_out_r2;
endmodule

波形检测

异步FIFO

面试真题

词频检测

题目描述： 使用verilog设计实现一个模块，对长度为byte(8 bits)的单词进行词频检测。假设每周期输入一个单词，共4096个单词,统计每个单词的出现次数，可以不考虑电路的输出。面试时不要求写出代码，只要求给出思路，口头描述电路的构成。

当时初步回答是，不同单词的编码本身可以看作单词的地址，用这个地址可以将单词分开，不考虑面积的情况下，可以在一个256to1的mux后接256个counter,每收到一个单词，将对应位置的counter+1。面试官进一步追问，如果考虑面积开销，应该怎样优化。回答：counter换成memory或register file），然后增加一级流水线，每收到一个单词将对应位置的数据读出，然后将该数据+1，下个周期将该数据写回，同时读入一个新的数据。如果连续2个周期出现同一个单词的地址冲突，考虑数据的forwarding,将来不及写回的数据作为读数直接+1。

参考设计代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
module wordcounts (
    input [7:0] data_in,
    input   clk,
    input   rst_n
);
    reg [12:0]    word_counts;
    wire [12:0]  read_data[255:0];
    wire [255:0]   write_en;
    genvar  i;
   
    generate
        for (i=0 ;i<256;i=i+1 ) begin
            assign write_en[i] = (data_in == i[7:0]);
            sim_dfflr #(13) counter(word_counts+ 1'b1,  read_data[i] ,write_en[i],clk,rst_n);
        end
    endgenerate
    assign word_counts = read_data[data_in];
    
endmodule



module sim_dfflr #(
    N=8
) (
    input[N-1:0] din,
    output reg[N-1:0] qout,
    input load_en,
    input clk,
    input rst_n
);
    always @(posedge clk or negedge rst_n) begin
        if(!rst_n)
            qout <= {N{1'b0}};
        else if (load_en)
            qout <= din;
    end
endmodule

思路是先定义寄存器，然后使用generate语句生成一个寄存器堆。对应的data_in作为load_en信号使能对应位置寄存器进行写操作。这里不需要考虑地址冲突时的bypass问题，因为事实上并不是先读后写，而是第一种，计数器加上mux的思路（读操作并没有耗费一个周期的时间）。
因此下面这种写法更直观：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
module wordcounts (
    input [7:0] data_in,
    input   clk,
    input   rst_n
);
    wire [12:0]  read_data[255:0];
    wire [255:0]   write_en;
    genvar  i;
   
    generate
        for (i=0 ;i<256;i=i+1 ) begin
            assign write_en[i] = (data_in == i[7:0]);
            sim_dfflr #(13) counter( read_data[i]+ 1'b1,  read_data[i] ,write_en[i],clk,rst_n);
        end
    endgenerate
    
endmodule

对应的testbench如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
module tb_top;

    `define CLK_PERIOD  10
    logic clk;
    logic rst_n;
    logic[7:0] data_in;
    class word;
        rand byte data;
        logic [12:0]  counts[256];

        function counts_init;
            foreach (this.counts[i])begin
                counts[i] = 13'b0;
            end
        endfunction

        task  data_gen(input clk, output[7:0] data_out);
            this.randomize();
            data_out = this.data;
            $display("generate ramdom words：%c ",this.data);
            counts[data_out] += 13'b1;
        endtask //
    endclass 

    word test_word = new();

    initial begin
        clk=1'b0;
        rst_n = 1'b0;
        #1 rst_n = 1'b1;
        # (4097*`CLK_PERIOD)
        for (int i = 0;i<256 ;i++ ) begin
            if (test_word.counts[i]==u_wordcounts.read_data[i])
                $display("word %2h count right,number:%d",i,test_word.counts[i]);
            else $display("word %2h count wrong! generate %d, counts %d",i,test_word.counts[i],u_wordcounts.read_data[i]);
        end
        $finish();
    end

    initial begin
            forever #(`CLK_PERIOD/2) clk = ~clk;  
    end

    initial begin
        test_word.counts_init();  
        $display("wait for reset");
        @(posedge rst_n);  
        $display("reset success");
        fork
        forever begin
            @(posedge clk);
            test_word.data_gen(clk, data_in);
        end
        join_none
        
    end

    initial begin
        $fsdbDumpfile("tb_top.fsdb");
        $fsdbDumpvars(0, tb_top, "+mda");
    end

    wordcounts u_wordcounts(
        .data_in (data_in ),
        .clk     (clk     ),
        .rst_n   (rst_n   )
    );

endmodule

测试结果如下：

独热码检测

题目描述：并行输入的16bit数据，判断其是否为one-hot(即只有一位是1，其余位都是0).

思路：

  1. 如果是纯组合逻辑，可以进行逐位亦或。如果是onehot,则逐位亦或的结果必定为从高到低全1，后半部分全0的情况(例如，16’h01的结果会是，16’hfe,16’h02的结果会是16’hfb)。此外，根据原始独热码1的位置，可以判断出逐位亦或得到的第一个1的位置。
  2. 此外由于只有16种情况，也可以考虑查表
  3. PPA优化，考虑分治，每4bit进行单独判断，最后的4个结果再进行一次独热判断
1
2
3
4
5
6
7
8
9
10
11
12
13
14
module is_onehot(
    input [15:0] data,
    output is_onehot
);

    wire [15:0] masked_data;

    genvar i;
    assign masked_data[0]=1'b0;
    for(i=0;i<15;i=i+1)begin: mask
        masked_data[i+1] = data[i] ^ masked_data[i];
    end

    assign is_onehot = masked_data[15] & ( &( masked_data[14:0] | ~data[14:0]) );

轮询仲裁

题目描述：实现对4个请求的轮询仲裁。假设有abcd 4个端口，一开始a具有最高优先级，a得到资源后其优先级变为最低，以此类推。

思路： 构建优先级矩阵。4个变量两两一组需要6个偏序关系，所以实际上是一个上三角矩阵。矩阵中每个寄存器的1或0代表优先级的相对高低。之后每个cycle根据仲裁结果进行优先级关系的调整。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
module arbiter(
    input grant_a,
    input grant_b,
    input grant_c,
    input grant_d,
    output sel_a,
    output sel_b,
    output sel_c,
    output sel_d,
    input clk,
    input rst_n
); 

    reg prio_a_b;
    reg prio_a_c;
    reg prio_a_d;
    reg prio_b_c;
    reg prio_b_d;
    reg prio_c_b;

写太多遍了，略。

固定优先级仲裁

题目描述：实现任意比特的固定优先级仲裁。优先级从最高位到最低位逐位递减。

思路：纯组合逻辑直接实现就好了。从高到低依次优先级判断。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
module prio_arbiter #(
    parameter N =16 
) (
    input   [N-1:0] req_in,
    output  [N-1:0] grant_out
);
    
    wire [N:0]    granted;
    wire [N-1:0]    grant;

    assign granted[N]   = 1'b0;
    genvar i;
    generate
        for (i = N-1;i>=0 ; i=i-1 ) begin
            assign grant[i] = req_in[i] & ~ granted[i+1];
            assign granted[i] = grant[i] | granted[i+1];
        end
    endgenerate

    assign grant_out = grant;
endmodule

开放性问题

  1. 平时的学习工作中如何学习？

  2. 今后想从事的方向？

  3. 学校中学习的课程？

  4. 自我评价一下，你认为自己的优劣势有哪些？

  5. 我看你的经历里有很多xxx方向的工作，如果入职后从事yyy相关的工作可以吗？